Логика высказываний – очень узкая логическая теория. Есть такие типы логических рассуждений, которые не могут быть осуществлены в рамках логики высказываний. Например:
1. Всякий друг Ивана есть друг Петра. Павел не друг Ивана, следовательно, Павел не друг Петра.
2. Простое число 2 – четное, следовательно, существуют четные простые числа.
Корректность таких выводов базируется не только на истинности соответствующих предложений, но и на смысле слов «всякий» и «существуют». Чтобы сделать более понятной структуру сложных высказываний используют специальный язык – язык предикатов первого порядка.
Предикаты
Рассмотрим предложения, зависящие от параметров:
Х – четное число.
X<Y
X+Y=Z
X,Y – братья.
Если заменить переменные X, Y, Z некоторыми конкретными значениями, то мы получим определенные высказывания, которые могут быть истинными или ложными.
Например:
3 – четное число.
2<5
2+3=5
Иван и Павел – братья.
Предложения такого рода называются предикатами.
Предикат Р(х1,…,хn) – функция, переменные которой принимают значения из некоторого множества M, а сама функция принимает значение истина (1) или ложь (0).
Р(х1,…,хn): Mn®{0,1}
Высказывания - это 0-местные предикаты. Над предикатами выполняются логические операции, в результате чего получаются новые предикаты.
С каждым предикатом связано число, которое называется местностью или арностью предиката (количество переменных).
Язык предикатов – наиболее приближенный к естественным языкам формальный математический язык.
Примеры:
1. Р(х) – х делится на 2
Q(x) – x делится на 3
P(x)&Q(x) – x делится на 2 и 3, т. е. определен предикат делимости на 6.
2. S(x,y) – x равно y.
S(x,y)& S(y,z)®S(x,z)
Кроме операций логики высказываний, к предикатам можно применять операции связывания кванторами.
1. Квантор общности (
).
- высказывание истинное для каждого 
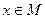, т. е. это высказывание не зависит от xi.
2. Квантор существования (
).
- высказывание истинно, если существует 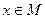, для которого это высказывание истинно.
Для конечных множеств операции навешивания кванторов можно выразить через операции & и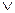 
.
Пусть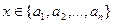 
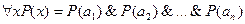
На языке предикатов можно составить более сложные высказывания, чем на языке логики высказываний.
Исчисление предикатов
Исчисление предикатов первого порядка – это формальная теория K, в которой определены:
1. Алфавит:
· Связки: 
(основные), &, 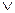(дополнительные).
· Служебные символы: (,).
· Кванторы , .
· Предметные константы a,b,c,….
· Предметные переменные x, y, z,….
· Символы предикатов P,Q,R,….
· Символы функций f, g, h,….
Константы, переменные, функторы – называются термами.
2. Формулы. Слово называется формулой, если оно имеет следующий синтаксис:
1) Р(х1,…,хn) – атомарная формула (А).
Вхождения переменных в атомарную формулу называются свободными.
2) Если А – формула, то 
- тоже формула.
3) Если А и В – формулы, то 
- формулы.
4) Если А – формула, содержащая свободную переменную х, то 
- формулы.
Слово является формулой, если это следует из 1-4.
Вхождения переменных в формулах называются связанными, переменные не равные х остаются свободными.
Пример
- х – свободная переменная, у – связанная переменная.
Формула, не содержащая свободных переменных, называется замкнутой.
3. Аксиомы (логические).
1) Любая система аксиом исчисления высказываний.
А1: 
А2: 
А3: 
2) Собственные аксиомы.
P1: 
,
P2: 
,
где t – терм.
4. Правила вывода.
1. 
,
2. 
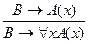- введение квантора общности,
3. 
- введение квантора существования.
Исчисление предикатов, в котором кванторы могут связывать только предметные переменные и не могут связывать функторы или предикаты называется исчислением первого порядка.
Интерпретация
Интерпретация I исчисления предикатов K с областью интерпретацией M – это набор функций, который сопоставляет:
· каждой предметной константе a элемент I(a)ÎM;
· каждому n-местному функтору f операцию I(f):Mn®M. 
· каждому n-местному предикату Р отношение I(P)Ì Mn.
Для нас имеют смысл только интерпретированные предикаты, т. е. те, которым поставлены в соответствие некоторые отношения (для одноместных предикатов – свойства).
Пример.
Рассмотрим 3 формулы.
1. P(x,y)
2. 
3. 
В качестве области интерпретации возьмем множество целых положительных чисел и интерпретируем P(x,y) как отношение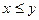 
.
Тогда формула 1 – это предикат 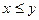. Он принимает значение истинно при любых a,b принадлежащих множеству целых положительных чисел, если 
.
Формула 2 – это предикат, который принимает значение истинно при x=1, т. е. он выражает свойство, что для каждого положительного целого числа y .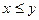
Формула 3 – это предикат, который всегда будет истинен. Он выражает свойство: существует положительное целое число y, для которого .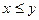
Формула называется истинной, если она выполняется на любом наборе элементов М.
Формула называется ложной, если она не выполняется на любом наборе элементов М.
Формула общезначима (тавтология), если она истинна в любой интерпретации.
Теорема: Любая выводимая в исчислении предикатов формула – общезначима.
