Задачу алгоритмической разрешимости можно сформулировать следующим образом: задача алгоритмически разрешима, если для нее можно построить рекурсивную функцию (машину Тьюринга, λ – нотацию, алгорифм Маркова).
Машины Тьюринга
Машина Тьюринга (МТ) – это математическая модель идеализированного вычисляемого устройства. Для построения МТ надо задать:
1. Конечный алфавит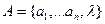 
, где 
- пустой символ.
2. Конечное множество внутренних состояний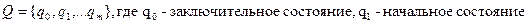 
.
МТ представляет собой
· Бесконечную ленту, разделенную на ячейки. В каждый момент времени в ячейке записана буква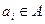 
. В процессе работы в ячейку может быть записан другой символ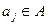 
· По ячейкам передвигается управляющее устройство (УУ). В каждый момент времени оно находится напротив какой-то ячейки и имеет некоторое состояние 
.
Машина действует дискретно, т. е. в определенные моменты времени.
Если в какой-то момент времени УУ воспринимает ячейку, содержащую символ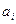 
и МТ находится в состоянии 
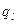, то МТ может совершить следующие действия:
1. Стереть символ 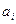и записать на его место символ 
.
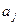2. Переместиться в ячейку слева (Л).
3. Переместиться в ячейку справа (П).
4. Остаться на месте (С).
Эти действия называются программой.
Таким образом, М=<A,Q, П>.
Программу МТ можно представить в виде последовательности команд вида: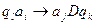 
,
где D={Л, П, С}. (Л- переход влево, П – переход вправо, С – остаться на месте).
Программу также можно представить в виде таблицы:
| q1 | q2 | …. | qn | |
| a1 | ||||
| a2 | ||||
| …. | 
| |||
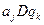
| am |
Пример. МТ добавляет к слову единицу.
|
|
|
|
|
Программа:
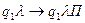(Если в воспринимаемой ячейке символ , и МТ находится в состоянии q1, то состояние не меняется, символ не меняется, УУ сдвигается вправо).
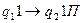(Если в воспринимаемой ячейке символ 1, и МТ находится в состоянии q1, то это значит, что УУ находится на начале слова, состояние меняется на q2, символ не меняется, УУ сдвигается вправо).
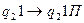(Если в воспринимаемой ячейке символ 1, и МТ находится в состоянии q2, то это значит, что УУ передвигается по слову, состояние не меняется, символ не меняется, УУ сдвигается вправо).
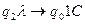(Если в воспринимаемой ячейке символ , и МТ находится в состоянии q2, то это значит, что УУ дошло до конца слова, состояние меняется на заключительное, символ меняется на 1, УУ останавливается).
В виде таблицы эту программу можно записать следующим образом:
| q1 | q2 | |
|
| 
| 
|
|
|
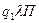
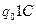
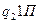
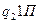
Конфигурация МТ (машинное слово) – это слово вида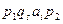 
, где
p1 – слово в алфавите МТ (может быть пустое),
qs – внутреннее состояние М,
ai – воспринимаемый символ,
p2 – слово в алфавите МТ.
МТ переводит конфигурацию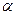 
в конфигурацию 
(
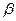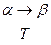), если 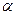имеет вид 
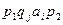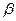, имеет вид 
, 
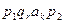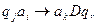- одна из команд МТ.
Для рассмотренного выше примера:
1. Команда 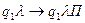переводит МТ из конфигурации 
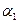в конфигурацию 
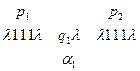
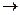
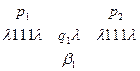
2. Команда 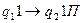переводит МТ из конфигурации 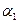в конфигурацию
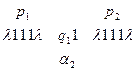
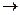
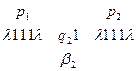
и т. д.
МТ останавливается при конфигурации 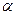, если не существует такой конфигурации 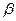, что 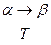(т. е. 
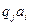входит в 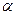, а среди команд МТ нет такой, которая бы начиналась с ).
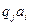Тезис Тьюринга: Любой интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга.
Рекурсивные функции
Будем рассматривать только числовые функции, т. е. функции, аргументы и значения которых принадлежат множеству натуральных чисел N (N=0,1,2,…).
Если область определения функции совпадает с множеством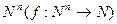 
, то функция называется всюду определенной, иначе – частично определенной.
Пример:
f(x,y)=x+y – всюду определенная функция,
f(x,y)=x-y – частично определенная функция, т. к. она определена только для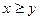 
.
Рекурсивное определение функции – это такое определение, при котором значение функции для данных аргументов определяется значениями той же функции для более простых аргументов или значениями более простых функций.
Примеры:
1. Числа Фибоначчи (1, 1, 2, 3, 5, 8, …) это последовательность чисел f(n), где f(0)=1, f(1)=1, f(n+2)=f(n)+f(n+1).
2. Факториал (n!=1*2*3*…*n) f(0)=1, f(n+1)=f(n)*(n+1).
Рекурсивные функции строятся на основе трех примитивных (заведомо однозначно понимаемых и реализуемых) функций. Их также называют простейшими.
1. S(x)=x+1 – функция следования.
Примеры: S(0)=1, S(1)=2, S(-5) – не определена.
2. О(х)=0 – нуль-функция;
Примеры: О(0)=0, О(1)=0, О(-5) – не определена.
3. Im(x1,x2,…,xn)=xm, (m=1,2,…n) – функция проектирования (выбора аргумента).
Пример: I2(1,2,3,4,…n)=2.
С примитивными функциями можно производить различные манипуляции, используя три оператора: суперпозиции, примитивной рекурсии и минимизации.
1. Оператор суперпозиции (подстановки).
Пусть f – m-местная функция, g1,…gm – n-местные операции на множестве N. Оператор суперпозиции S ставит в соответствие операциям f и g1,…gm n-местную функцию h.
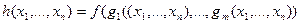
Примеры:
1) Используя оператор суперпозиции, можно получить любую константу.
S(O(x))=0+1=1
S(S(O(x)))=0+1+1=0+2=2
S(S…(O(x))…)=0+n, где число вложений функций следования n.
2) Используя оператор суперпозиции, можно выполнить сдвиг на константу n.
S(x)=x+1
S(S(x))=x+1+1=x+2
S(S…(S(x))…)=x+n.
2. Оператор примитивной рекурсии
Оператор R каждой (n+2)-местной операции f и n-местной операции g ставит в соответствие (n+1)-местную операцию h=R(f,g), удовлетворяющую следующей схеме:
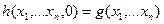
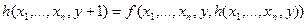
Для n=0 схема примитивной рекурсии имеет вид:
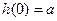, где а – константа,
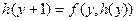
Пример: Вычисление факториала с использованием оператора примитивной рекурсии будет выглядеть следующим образом.
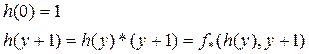
Схема примитивной рекурсии образует процесс построения функции h, при котором на нулевом шаге используется функция g, а на каждом последующем шаге значение функции f от аргументов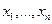 
, номера y предыдущего шага и значения функции h, вычисленного на предыдущем шаге.
Функция называется примитивно-рекурсивной (ПРФ), если она может быть получена из простейших функций с помощью оператора суперпозиции или оператора примитивной рекурсии.
Примеры:
1) 
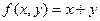- примитивно-рекурсивная функция.
Схема примитивной рекурсии:
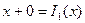
2) 
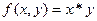- примитивно-рекурсивная функция.
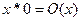
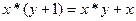
3. Оператор минимизации (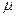
-оператор)
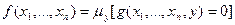, где y – выделенная переменная.
Работу 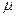-оператора можно описать следующим образом. Выделяется переменная y, затем фиксируются остальные переменные 
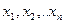. Значение у последовательно увеличивается, начиная с 0. Значением 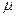-оператора будет то значение у, при котором функция впервые обратилась в 0.
Если функция не обратилась в 0 или принимает отрицательное значение, то значение 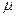-оператора считается неопределенным.
Пример: g(x,y)=x-y+3;
Зафиксируем х=1 и будем менять y.
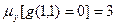, т. к. 1-1+3=3
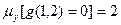, т. к. 1-2+3=2
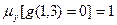, т. к. 1-3+3=1
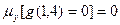, т. к. 1-1+3=0
Следовательно,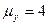 
.
Функция f(x1,x2,…,xn) называется частично рекурсивной (ЧРФ), если она может быть получена из простейших функций с помощью конечного числа применений операций суперпозиции, примитивной рекурсии и минимизации.
Пример.
f(x,y)=x-y - частична, т. к. она не определена, если x<y. Чтобы сделать эту функцию полностью определенной на множестве натуральных чисел N, рассматривают усеченную разность.
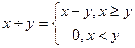
Свойства усеченной разности.
1) 
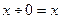
2) 
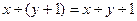
3) 
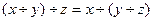
- Докажем, что
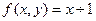- примитивно-рекурсивная функция.
Функция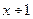 
примитивно рекурсивна, т. к. по схеме примитивной рекурсии:
1) При х=0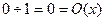 
.
2) 
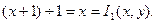
Т. о. ее можно получить из простейших функций О(х) и Im(x1,…xn) с помощью оператора простейшей рекурсии R.
- Докажем, что
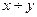- примитивно-рекурсивная функция.
По схеме примитивной рекурсии
1) 
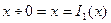
2) 
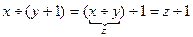
Т. о. функцию 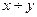можно получить с помощью операции примитивной рекурсии из функций 
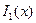и h(x,y,z)= 
.
- Функция
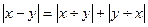также является примитивно-рекурсивной -
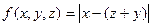- примитивно-рекурсивная функция. - Функцию f(x,y)=x-y можно получить с помощью оператора минимизации:
.
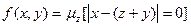Следовательно, функция f(x,y)=x-y является частично-рекурсивной функцией.
Всюду определенная частично-рекурсивная функция является общерекурсивной (ОРФ).
Для алгоритмических проблем типичной является ситуация, когда требуется найти алгоритм для вычисления числовой функции f(x1,…xn). Числовые функции, значения которых можно вычислить с помощью некоторого алгоритма, называются вычислимыми функциями. Это понятие интуитивно, т. к. интуитивно понятие алгоритма.
Функция f(x1,…xn) эффективно вычислима, если существует алгоритм, с помощью которого можно найти f(k1,…kn), если известны k1,…kn.
Тезис Черча. Всякая эффективно вычислимая функция является частично-рекурсивной функцией.
В формулировку тезиса Черча входит понятие эффективной вычислимости. Поэтому его нельзя ни доказать, ни опровергнуть в математическом смысле.
Частичная рекурсивность – это уточнение понятия вычислимой функции. С его помощью можно уточнять или опровергать вычислимость.
Любая частично-рекурсивная функция является вычислимой по Тьюрингу и наоборот.
