ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ
«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
В Г. ТАГАНРОГЕ РОСТОВСКОЙ ОБЛАСТИ
ПИ (филиал) ДГТУ в г. Таганроге
Кафедра гуманитарных и естественнонаучных дисциплин
АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Программа, методические указания и контрольные задания для студентов – заочников направления 09.03.02 «алгебра и аналитическая геометрия»
по курсу «Математика»
(бакалавриат)
Г.
Целями освоения дисциплины «алгебра и аналитическая геометрия» являются:
1. Теоретическое и практическое изучение обучающимися основных разделов математики, составляющих научную базу, на которой строится естественнонаучная и профессиональная подготовка будущих специалистов. способных выполнять все виды профессиональной деятельности, предусмотренные ФГОС ВПО для данных направлений, формирования математической составляющей общекультурных и профессиональных компетенций;
2. Обеспечение высокого уровня фундаментальной подготовки по математике как основы формирования общенаучных, профессиональных, социально-личностных и общекультурных компетенций;
3. Развитие у студентов личностных качеств и способностей успешно работать в новых, быстро развивающихся областях науки и техники, самостоятельно непрерывно приобретать новые знания, умения и навыки;
4. Вариативность формирования необходимых компетенций посредством различного уровня изучения дисциплины «Линейная алгебра».
Для достижения цели ставятся следующие задачи:
1. Воспитание культуры современного математического мышления;
2. Изучение математического аппарата, методов математического анализа, анализа состояния научно-технической проблемы на основе подбора и изучения литературных источников;
3. Моделирования объектов и процессов с целью анализа и оптимизации их параметров с использованием имеющихся средств исследования;
4. Формирование представления о математике как о мощном средстве решения задач в практической деятельности;
5. Привитие навыков использования математических методов для решения прикладных задач в профессиональной сфере;
6. Выработка навыков и умений самостоятельного расширения и углубления математических знаний и проведение математического анализа задач в профессиональной сфере.
Связь с предшествующими и последующими дисциплинами.
Для успешного освоения дисциплины, обучающиеся должны иметь базовую подготовку по дисциплине «Математика» в объеме программы средней школы.
Компетенции обучающегося:
Студенты, завершившие изучение дисциплины «Математика», должны обладать следующими вузовскими (обобщёнными) компетенциями (ВК):
1. Общекультурной компетенцией (ВОК) - способностью и готовностью приобретать с большой степенью самостоятельности новые знания в области математики, используя современные образовательные и информационные технологии;
2. Профессиональной компетенцией (ВПК):- способностью применять математический аппарат, методы математического анализа на уровне, необходимом для решения задач, имеющих естественнонаучное содержание и возникающих в сфере профессиональной деятельности.
Структура и содержание дисциплины
| Раздел (название) | Тема, литература | Содержание |
| Линейная алгебра | 1.1 Определители. [6.1.1, § 1], [6.1.10, гл.7] | Свойства, вычисление. |
| 1.2 Матрицы [6.1.1, § 3], [6.1.10, гл 7] | Типы матриц, операции над матрицами, ранг матрицы, обратная матрица, собственные значения. | |
| 1.3. Системы линейных уравнений, [6.1.1, § 2, 3], [6.1.10, гл 7] | Решение и исследование линейных систем. Теорема Кронекера-Капелли, метод Гаусса, правило Крамера. Матричная запись линейной системы. Основная и расширенная матрица линейной системы, определитель системы, базисные и свободные переменные. | |
| 1.4. Квадратичные формы [6.1.1, § 23] | Квадратичная форма в двухмерном пространстве, приведение ее к каноническому виду | |
| 1.5 Линейные отображения [6.1.1, § 15] | Определение линейного оператора, его матрица. | |
| Векторна я алгебра | 2.1. Векторы и операции над ними [6.1.1, §§ 5, 6, 12, 13], [6.1.10, гл 10] | Основные определения: модуль, направляющие косинусы, проекция вектора на ось. Линейная комбинация, координаты вектора в данном базисе, коллинеарные и компланарные вектора. Базис на плоскости и в пространстве. Линейные операции и их свойства. Скалярное, векторное и смешанное произведение векторов. Условия коллинеарности, перпендикулярности и компланарности векторов, угол между векторами. |
| 2.2. Элементы теории множеств [7.1.1 § 3] | Множество, способы задания, основные числовые множества, подмножество, мера плоского множества, основные свойства отображений множеств, операции над множествами. | |
| 2.3. Векторное пространство, евклидово пространство [6.1.1 § 6] | Понятие п -мерного вектора и векторного пространства. Линейное пространство, норма вектора | |
| Комплекс-ный анализ | 3.1. Комплексные числа [6.1.2 гл. 7 §§ 1-3], [6.1.10 гл 9] | Алгебраическая и тригонометрическая форма, геометрическая интерпретация, модуль и аргумент комплексного числа. Операции над комплексными числами. |
Перечень вопросов для подготовки к экзаменам.
1. Множества. Операции над множествами.
2. Декартово произведение множеств. Покрытие множества.
3. Символы математической логики.
4. Множество R. вещественных чисел. Свойство плотности множества R
5. Теорема Архимеда и следствие из неё.
6. Теорема о приближении иррациональных чисел рациональными числами.
7. Свойства действительных чисел.
8. Грани числовых множеств. Существование точной верхней и точной нижней грани.
9. Числовая прямая и множества на ней.
10. Абсолютная величина действительного числа и его свойств.
11. Прямоугольные декартовы координаты на плоскости и в пространстве.
12. Полярная система координат на плоскости и её связь с декартовой системой.
13. Сферические и цилиндрические координаты точки в пространстве E3.
14. Преобразование координат на плоскости.
15. Понятие матрицы и виды матриц.
16. Линейные операции над матрицами и их свойства.
17. Транспонирование матриц.
18. Элементарные преобразования матриц. Приведение матрицы к каноническому виду.
19. Произведение матриц. Обратная матрица.
20. Определители и их свойства. Вычисление определителей второго и третьего
порядка.
21. Разложение определителя по элементам строки или столбца. Правило Лапласа.
22. Присоединённая матрица и условие существования обратной матрицы A-1. Свойства матрицы A-1.
23. Ранг матрицы и его свойства.
24. Общий вид системы линейных алгебраических уравнений(СЛАУ). Решение СЛАУ.
25. Теоремы о существовании и единственности решения СЛАУ. Правила решения СЛАУ.
26. Метод обратной матрицы решения СЛАУ. Правило Крамера.
27. Метод Гаусса решения СЛАУ.
28. Однородные СЛАУ и их решения.
29. Собственные числа и собственные векторы матрицы. Характеристическая матрица и характеристический многочлен.
30. Векторы, модуль вектора. Свободные векторы.
31. Линейные операции над векторами и их свойства.
32. Линейно зависимые и независимые векторы.
33. Базис векторов. Координаты вектора в базисе.
34. Условие коллениарности двух векторов.
35. Скалярное произведение двух векторов и его свойства. Ортогональность векторов.
36. Прямоугольная декартова система координат 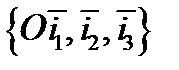 в E3 .
в E3 .
37. Угол между векторами. Неравенство Коши-Буняковского.
38. Векторное произведение двух векторов и его свойства.
39. Смешанное произведение трёх векторов и его свойства. Объём пирамиды.
40. Радиус-вектор точки. Координаты вектора.
41. Расстояние между двумя точками.
42. Понятие п -мерного вектора и векторного пространства.
43. Линейное пространство
44. Норма вектора
45. Нормированное пространство
46. Комплексные числа и действия с ними. Модуль и аргумент комплексного числа.
47. Тригонометрическая форма комплексного числа.
48. Формула Эйлера.
49. Показательная форма комплексного числа.
50. Формула Муавра.
51. Корни из комплексных чисел.
52. Теорема Безу.
53. Основная теорема алгебры.
54. Деление отрезка в данном отношении.
55. Уравнение линии на плоскости E2. Линии первого порядка. Уравнение прямой с угловым коэффициентом.
56. Общее уравнение прямой на плоскости.
57. Уравнение прямой в E2, проходящей через точку перпендикулярно вектору.
58. Уравнение прямой на плоскости, проходящей через две данные точки. Уравнение прямой в E2 в отрезках на осях координат.
59. Нормальное уравнение прямой на плоскости.. Расстояние от точки до прямой.
60. Параметрические уравнения прямой. Угол между прямыми в Е2.
61. Окружность и эллипс. Уравнение эллипса. Эксцентриситет эллипса.
62. Гипербола и её уравнение.
63. Парабола и её уравнение.
64. Общее уравнение кривой второго порядка и его приведение к каноническому виду.
65. Уравнение поверхностей и линий в пространстве Е3. Уравнение плоскости в Е3.
66. Уравнение плоскости, проходящей через три точки.
67. Уравнение плоскости в отрезках на осях координат.
68. Нормальное уравнение плоскости. Расстояние от точки до плоскости.
69. Угол между двумя плоскостями. Условие параллельности и перпендикулярности
двух плоскостей.
70. Параметрические уравнения прямой в Е3.
71. Каноническое уравнение прямой в Е3.
72. Уравнение прямой Е3, проходящей через две данные точки.
73. Общее уравнение прямой в Е3.Угол между двумя прямыми в Е3. Условие перпендикулярности прямой и плоскости.
74. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямых. Точка пересечения прямой и плоскости.
75. Поверхности второго порядка в Е3. Цилиндрические поверхности.
76. Конические поверхности и поверхности вращения.
77. Сфера и эллипсоид.
78. Однополостный гиперболоид.
79. Двуполостный гиперболоид.
80. Эллиптический и гиперболический параболоиды.
Литература.
| № | Автор | Название | Издательство | Год издания |
| 6.1.1 | Шевченко Н.П. | Алгебра и аналитическая геометрия | ДГТУ. - Ростов н/Д | |
| 6.1.2 | Зубков А.Н., Павлова М.Н | Матрицы и их применение. Линейные преобразования. | ДГТУ - Ростов н/Д | |
| 6.1.3 | Данко П.Е. | Высшая математика в упражнениях и задачах. Ч.1 | М.: ОНИКС 21 век: Мир и Образование | |
| 6.1.4 | Ворович Е.И. | Учебно-методическое пособие по подготовке к интернет экзамену | ДГТУ. - Ростов н/Д | |
| 6.1.5 | Шипачев В.С. | Задачник по высшей математике | М.: Высш. шк. | |
| 6.6.1 | Абуев Ф.Л. | Программа и варианты контрольных работ для студентов первого курса заочного факультета | ДГТУ. - Ростов н/Д | |
| 6.6.2 | Шевченко Н.П. | Программа, варианты и методические указания к контрольным работам для студентов второго курса заочного факультета | ДГТУ. - Ростов н/Д |
Вариант контрольной работы соответствует последней цифре номера зачетной книжки (нуль соответствует варианту №10)
Контрольная работа №1
Задание №1
1.Даны матрицы А =  и В =
и В =  .
.
Вычислить ВА+2В.
2.Даны матрицы А =  и В =
и В =  .
.
Вычислить АВ-3В.
3.Даны матрицы А =  и В =
и В =  .
.
Вычислить АВ- 3 А.
4.Даны матрицы А =  и В =
и В =  .
.
Вычислить 3 В + ВА.
5.Даны матрицы А =  и В =
и В =  .
.
Вычислить 2А + ВА.
6.Даны матрицы А =  и В =
и В =  .
.
Вычислить 3В + ВА.
7.Даны матрицы А =  и В =
и В =  .
.
Вычислить 2 В + 3ВА.
8.Даны матрицы А = 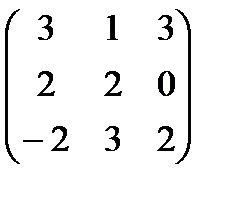 и В =
и В =  .
.
Вычислить 3В + 2 АВ.
9.Даны матрицы А =  и В =
и В =  .
.
Вычислить 3 В + ВА.
10.Даны матрицы А =  и В =
и В =  .
.
Вычислить 4А + ВА.
Задание №2
Решить системы линейных алгебраических уравнений матричным способом.
1.  6.
6. 
2.  7.
7. 
3.  8.
8. 
4.  9.
9. 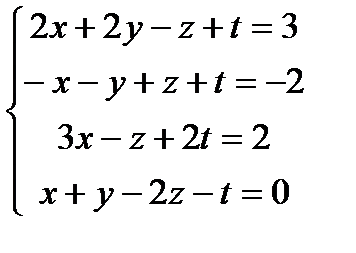
5. 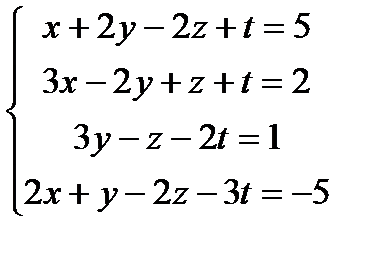 10.
10. 
Задание №3
Решить систему линейных алгебраических уравнений
методом Гаусса;
1.  2.
2. 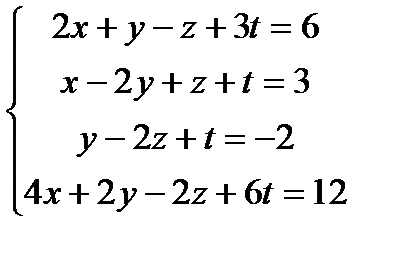
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
Задание №4
Найти собственные числа и собственные векторы матрицы А.
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7. 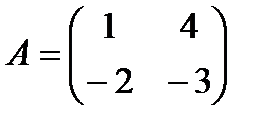 8.
8. 
9.  10.
10.  .
.
Даны точки А, В, С, D.
| № варианта | А | В | С | D |
| (2;-1;3) | (-1;3;2) | (0;1;-1) | (-1;-3;1) | |
| (-2;-1;3) | (1;3;2) | (3;1;-1) | (2;-3;-2) | |
| (0;-1;3) | (-2;3;-1) | (0;1;-1) | (-1;-3;1) | |
| (3;-2;3) | (-1;0;2) | (-3;1;-1) | (-3;-3;1) | |
| (1;-1-2) | (-1;2;-2) | (2;1;-2) | (-1;-2;3) | |
| (1;-1;3) | (-1;-2;2) | (1;1;-1) | (0;-3;1) | |
| (2;-2;3) | (-2;3;2) | (1;1;-1) | (-1;-3;0) | |
| (-2;1;-3) | (2;3;2) | (3;-1;-1) | (-1;-3;1) | |
| (-1;-1;3) | (-1;3;-2) | (-3;1;-1) | (-1;-3;2) | |
| (2;-1;2) | (-1;-3;2) | (2;1;-1) | (-1;-3;0) |
Задание №5.
Найти:
1)направляющие косинусы вектора  ;
;
2) проекцию пр 
 .
.
3) высоту h пирамиды АВСD, опущенную из вершины D на плоскость основания АВС
Задание №6.
Доказать, что вектора  образуют базис. Найти разложение вектора
образуют базис. Найти разложение вектора  в этом базисе.
в этом базисе.
Задание №7.
1) Составить уравнение прямой AB
2) написать параметрическое уравнение прямой L 1, проходящей через точку С, параллельно прямой AB;
3) написать уравнение высоты BH треугольной пирамиды ABCD;
4) написать уравнение медианы AD треугольника ABC;
5) определить угол между плоскостями ABC и ACD;
Задание №8.
Определить тип кривой второго порядка; найти координаты центра; полуоси.
1. 5 х 2 + 9 у 2 – 30 х + 18 у + 9 = 0
2. 16 х 2 - 9 у 2 – 64 х - 54 у - 161 = 0
3. 4 х 2 + 9 у 2 – 16 х - 18 у - 11 = 0
4. х 2 - 4 у 2 – 6 х + 16 у - 11 = 0
5. 16 х 2 + 25 у 2 + 32 х - 100 у - 284 = 0
6. 9 х 2 - 16 у 2 + 90 х + 32 у - 367 = 0
7. х 2 - 4 у 2 – 6 х - 16 у - 29 = 0
8. 4 х 2 + 3 у 2 – 8 х + 12 у - 32 = 0
9. 16 х 2 - 9 у 2 – 64 х - 18 у + 199 = 0
Задание №9.
Возвести комплексное число  в степень:
в степень:
1)  , ,  ; ;
| 3)  , ,  ; ;
|
2)  , ,  ; ;
| 4)  , ,  ; ;
|
5)  , ,  ; ;
| 8)  , ,  ; ;
|
6)  , ,  ; ;
| 9)  , ,  ; ;
|
7)  , ,  ; ;
| 10)  , ,  . .
|






