Расчетно-графическая работа № 5

Построение точки пересечения прямой и плоскости

Задание выполняется в соответствии с вариантом.

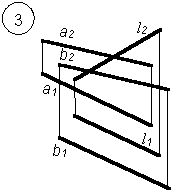
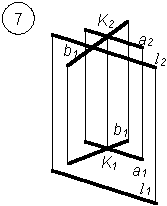
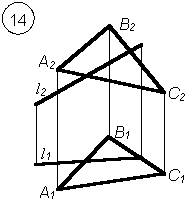
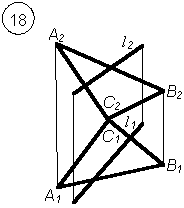
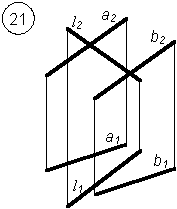
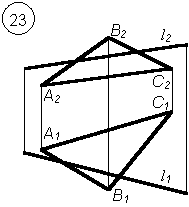
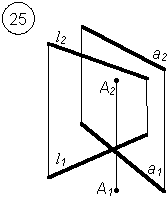
1. Построить точку пересечения прямой и плоскости общего положения.

1. Определить видимость прямой относительно плоскостей проекций.

Варианты заданий РГР № 5

 

 

Примечание. Образец выполнения расчетно-графической работы № 5 см. прил. 6

ТРЕНИНГ УМЕНИЙ

Задачи для самостоятельной работы

К главе 2

1. Построить комплексный чертеж произвольной точки А, находящейся во второй четверти пространства и удаленной от горизонтальной плоскости проекций на 32 мм и от фронтальной плоскости проекций – на 18 мм.

2. Построить комплексный чертеж точки А (10; –24; –13).

3. Дана точка А (15; 12; 20). Построить комплексный чертеж точки В, симметричной точке А относительно p₁, p₂; оси ОХ.

1. Построить комплексный чертеж точек (рис. 1).

Рис. 1

1. Построить наглядное изображение точек (рис. 2).

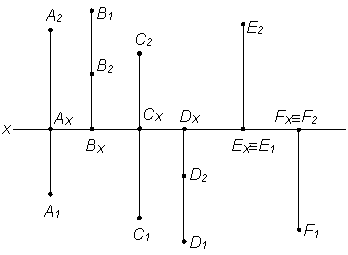
Рис. 2

К главе 3

1. Построить проекции прямой АВ (рис. 3), если она:

а) параллельна p₁;

б) параллельна p₂;

в) параллельна ОХ;

г) перпендикулярна p₁;

д) перпендикулярна p₂.

Рис. 3

2. Построить проекции отрезков по координатам. Определить их положение относительно плоскостей проекций: А(80; 40; 30), B(20; -15; 30), C(60, 40, -25), D(10; -40; -50), E(30; 0; 70), F(3; 40; 0).

3. Определить положение точек относительно прямой l (рис. 4).

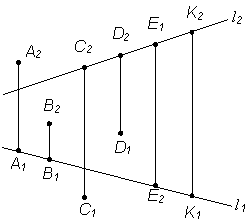
Рис. 4

4. Построить комплексный чертеж точки А, которая находится под прямой а; В – за прямой а; точки С, которая принадлежит прямой а.

5. Через точку А(А₁А₂) провести прямую h || p ₁ и через точку В(В₁В₂) провести прямую f || p ₂ (рис. 5).

Рис. 5

К главе 4

1. Через точку S провести прямую l|| а (рис. 6)

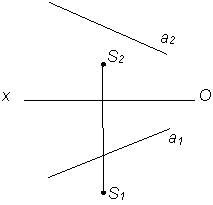
Рис. 6

1. Через точку S провести прямую l, пересекающую прямую а и параллельную p₁ (рис. 7).

Рис. 7

1. Выяснить взаимное положение двух прямых ab и cd (рис. 8):

Рис. 8

К главе 5

1. В плоскости, заданной двумя параллельными прямыми, построить фронталь на расстоянии 15 мм от p₁ (рис. 9):

Рис. 9

1. Построить произвольную точку К, принадлежащую плоскости D АВС (рис. 10):

Рис. 10

3. Задать произвольную горизонтально-проецирующую плоскость:

–двумя пересекающимися прямыми;

– прямой и точкой.

4. Задать плоскость, параллельную p₂:

– двумя параллельными прямыми;

– тремя точками.

1. Найти горизонтальную проекцию точки К, если она принадлежит плоскости, заданной AB|| CD (рис. 11):

Рис. 11

1. Построить недостающую проекцию l (l ₁) и точки D(D₂), принадлежащих плоскости D ABC (рис. 12):

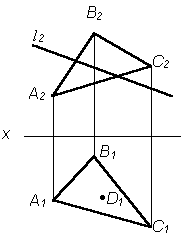
Рис. 12

К главе 6

1. Дана плоскость Р(а|| b) и фронтальная проекция m₂ прямой m, проходящей через точку D. Построить горизонтальную проекцию прямой m₁ так, чтобы прямая m была параллельна плоскости Р(а|| b) (рис. 13).

Рис. 13

2. Построить линию пересечения плоскости Р(D АВС) с плоскостью Q(DE EK) (рис. 14).

Рис. 14

3. Построить точку пересечения прямой m и плоскости Р (D АВС) (рис. 15).

Рис. 15

4. Через точку А (А₁А₂) провести прямую, перпендикулярную прямой m (рис. 16).

Рис. 16

5. Определить, перпендикулярна ли прямая l плоскости Q(a b) (рис. 17).

Рис. 17

Тесты

Тесты к главе 1

1. Укажите центральную проекцию точки А (рис. 1).

Рис. 1

2. Проецирование называется параллельным, если:

а) проецирующие лучи исходят из одной точки S;

б) все проецирующие лучи параллельны заданному направлению S;

в) все проецирующие лучи располагаются перпендикулярно плоскости проекций.

1. На каком чертеже (рис. 2) построена параллельная проекция отрезка АВ.

Рис. 2

4. Укажите, на каком чертеже (рис. 2) отрезок АВ проецируется в натуральную величину?

5. Может ли параллельная проекция отрезка прямой представлять собой точку?

1. На каком из чертежей (рис. 2) построена ортогональная проекция отрезка АВ?

Тесты к главе 2

1. Укажите, какая из точек А, В или С находится в третьей четверти: А(10; –15; –30); В(15; –20; 10); С(30; 10; –15).

2. Расстоянию точки А от плоскости p ₁ соответствует отрезок (рис. 3):

а) ОА_х;

б) А₁А_х;

в) А_хА₂.

Рис. 3

1. Какая из точек A; B; C; D; E; F находится во второй четверти (рис. 4)?

Рис. 4

4. Какая из точек на комплексном чертеже находится в третьей четверти (рис. 5)?

1. Какая из точек на комплексном чертеже принадлежит плоскости p ₂ (рис. 5)?

Рис. 5

Тесты к главе 3

1. Выберите соответствие обозначения отрезка АВ его изображению (рис. 6):

1. АВ || p 1 2. АВ || p 2 3. АВ ^ p 1 4. АВ ^ p 2 5. АВ || ОХ 6. АВ – общего положения	а		г
б		д
в		е

Рис. 6

2. На каком из комплексных чертежей отрезок АВ (рис. 6) проецируется в натуральную величину: а); б); в); г); д); е).

3. За прямой l расположена точка: А; B; C; D; E; K (рис. 7).

4. Прямой l принадлежит точка: А; B; C; D; E; K (рис. 7).

Рис. 7

Тесты к главе 4

Укажите, на каком из чертежей (рис. 8) прямые в пространстве

1) параллельны;

2) пересекаются;

3) скрещиваются.

Рис. 8

Тесты к главе 5

1. Укажите на каком из чертежей (рис. 9) задана плоскость уровня?

1. Укажите, на каком из комплексных чертежей (рис. 9) задана проецирующая плоскость?

Рис. 9

3. Укажите, на каком из чертежей (рис. 10)

– прямая l является горизонталью плоскости S (D АВС);

– прямая l является фронталью плоскости

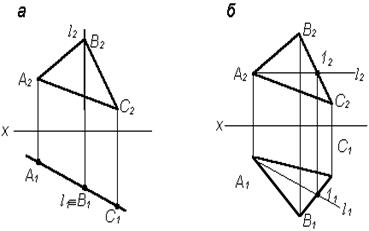
Рис. 10

4. На каком из чертежей (рис. 11) точка К принадлежит плоскости S (D АВС)?

Рис. 11

Тесты к главе 6

1. На каком из чертежей (рис. 12) плоскость S (D АВС) параллельна плоскости Р(m C n).

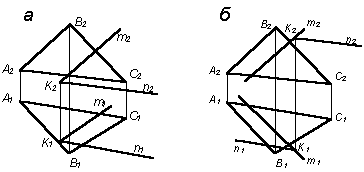
Рис. 12

2. Чтобы построить линию пересечения двух плоскостей общего положения необходимо использовать:

а) две вспомогательные прямые частного положения;

б) две вспомогательные плоскости общего положения;

в) две вспомогательные проецирующие плоскости.

3. Чтобы построить точку пересечения прямой и плоскости необходимо прямую заключить:

а) в плоскость общего положения;

б) в плоскость уровня;

в) в проецирующую плоскость.

4. Укажите, на каком чертеже (рис. 13) прямая l расположена параллельно плоскости P(a || b).

Рис. 13

5. Укажите, на каком из чертежей (рис. 14) прямая l перпендикулярна плоскости Q(a b)?

Рис. 14

Заключение

Итак, были подробно рассмотрены методы проецирования, точка в системе двух и трех плоскостей проекций, прямая и плоскость, взаимное положение прямых и плоскостей, а также некоторые позиционные задачи.

Даны методические рекомендации по изучению курса в целом и по выполнению расчетно-графических работ в частности.

Подробно рассмотрены примеры и алгоритмы решения различного рода задач. По каждой теме дан тренинг умений (решений задач) и заключительное тестирование. Для лучшего усвоения материала в конце учебного пособия представлен краткий словарь специальных терминов и определений.

Определены требования к знаниям и умениям, приобретаемым при изучении курса, виды контроля знаний студентов и их отчетности.

Во второй части планируемого пособия будут рассмотрены способы преобразования комплексного чертеже (метрические задачи), поверхности, точка на поверхности, пересечение прямой и поверхности, пересечение двух поверхностей и т.д.

ПРИЛОЖЕНИЯ

Приложение 1

Образец оформления листов формата А4
для выполнения расчетно-графических работ

Приложение 2

Образец выполнения графической работы №1

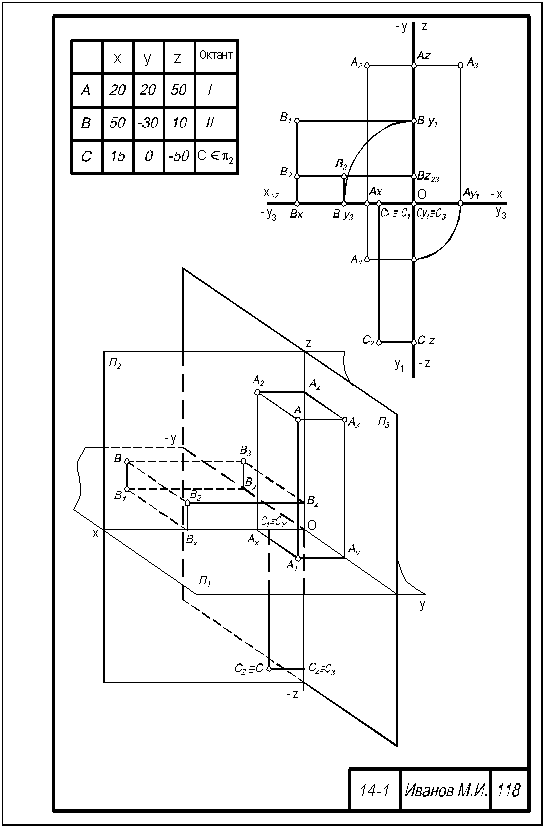
Приложение 3

Образец выполнения расчетно-графической работы №2

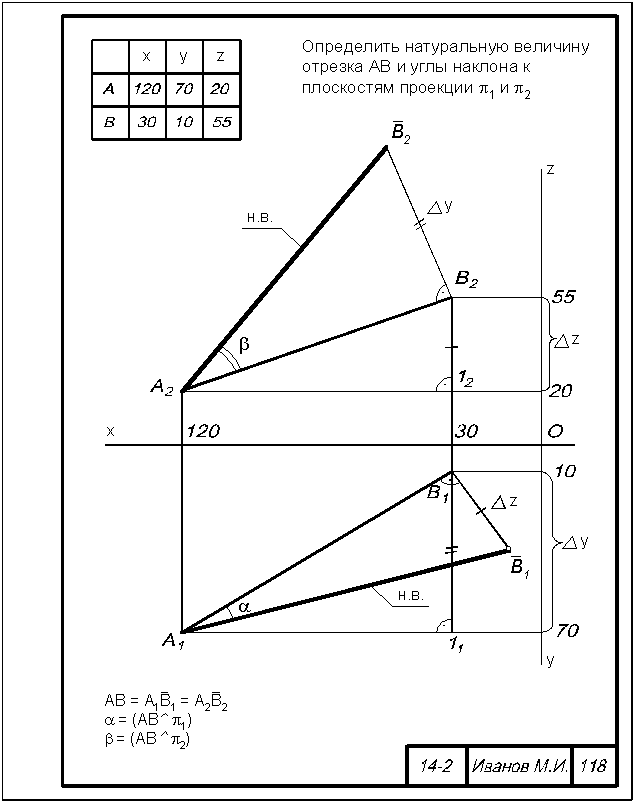
Приложение 4

Образец выполнения графической работы № 3

взаимное положение прямых в пространстве

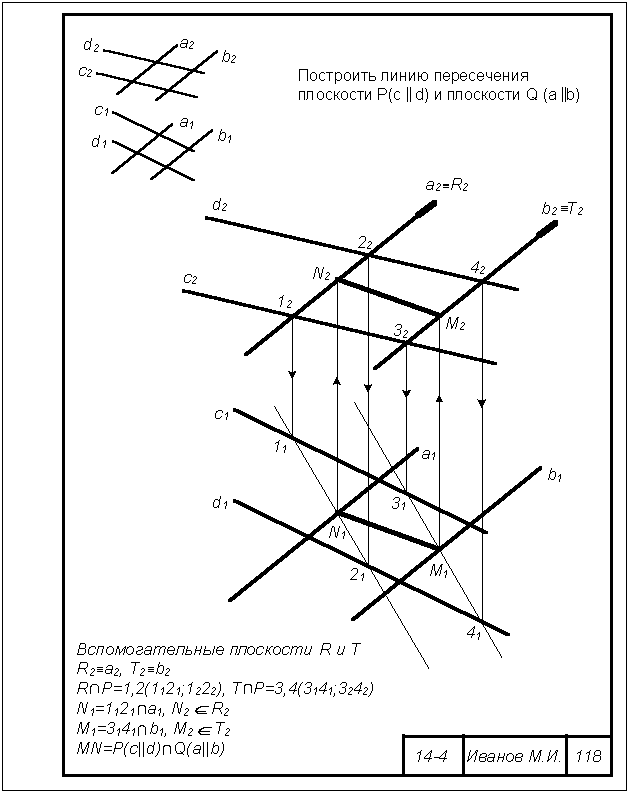
Приложение 5

Образец выполнения графической работы № 4

построение линии пересечения двух плоскостей

Приложение 6

Образец выполнения графической работы № 5

Построение точки пересечения прямой и плоскости

Краткий словарь
специальных терминов и определений

ГЕОМЕТРИЯ НАЧЕРТАТЕЛЬНАЯ. Раздел геометрии, в котором изучаются методы изображения пространственных форм на плоскости или другой поверхности. Проекционный метод построения изображений на плоскости распадается на следующие части: а) перспективу, б) аксонометрию (прямоугольную и косоугольную), в) эпюр Монжа, г) проекции с числовыми отметками. Главное место в начертательной геометрии занимает метод Монжа – ортогональное проецирование элементов трехмерного пространства на две взаимно-перпендикулярные плоскости, в результате которого получается двухкартинный плоский чертеж, обладающий метрической определенностью и обратимостью. Технические чертежи, выполненные этим способом, в зависимости от сложности изображаемой формы, могут иметь и бульшее число изображений (проекций).

ГОРИЗОНТАЛИ. 1. Линии на плоскости или поверхности, параллельные горизонтальной плоскости проекций. 2. Линии на карте, соединяющие точки одинаковой высоты; проведение горизонталей показывает рельеф местности.

ГОРИЗОНТАЛЬ ПЛОСКОСТИ. Прямая, принадлежащая данной плоскости и параллельная горизонтальной плоскости проекции.

ДЛИНА. Расстояние между конечными точками прямой. Определяется измерением с помощью масштабной единицы (эталона длины) и выражается некоторым положительным числом. В зависимости от выбора эталона длины изменяется и длина измеряемого отрезка. Следовательно, всякая длина – величина относительная. Длина должна обладать следующими свойствами: а) равные отрезки имеют равную длину; б) длина суммы двух отрезков равна сумме длин составляющих; в) существует отрезок, длина которого равна единице. Раздел геометрии, изучающий длину отрезка, называется лонгиметрией. Для практической деятельности во всех странах созданы эталоны длины (метр, ярд и др.)

ЗАДАЧА ПОЗИЦИОННАЯ. Геометрическая задача на построение точек или линий пересечения геометрических элементов, то есть задача на построение новой инциденции (принадлежности). Например, построение точки пересечения прямой и плоскости, построение теней и т.п. При решении позиционных задач не учитываются метрические свойства фигур, то есть те свойства, которые могут быть выявлены лишь в результате измерения.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ. Изображение предмета двумя или несколькими ортогональными проекциями с сохранением проекционной связи. Такой чертеж может быть выполнен: а) в основной системе с фиксированными осями проекции; б) в безосной системе; в) в системе с нефиксированными осями (с постоянной прямой чертежа).

КОМПОНОВКА ЧЕРТЕЖА (от лат. сomponare компоновать). Целесообразное размещение изображений, размеров и надписей на поле чертежа. Эстетическое восприятие также играет немалую роль при чтении чертежа: рабочему приятнее читать чистый и красивый чертеж, чем смотреть на грязный и плохо оформленный. Поэтому законы художественной композиции имеют прямое отношение к компоновке чертежей.

ЛИНИЯ (лат. linea). 1. Всякую линию можно представить себе как траекторию движущейся точки. Нельзя рассматривать линию как ряд точек; вместе с тем линия – это точечное множество. Все геометрические линии сплошные. На чертеже линии изображают условно (ГОСТ 2.303-68. Линии чертежа). 2. Линия – это множество всех последовательных положений движущейся точки. 3. Общая часть двух смежных областей поверхности. По определению Эвклида: “Линия же – длина без ширины”.

ОТРЕЗОК. Часть прямой, ограниченная с обеих сторон. Концы отрезка (точки) входят в отрезок. Отрезок следует обозначать либо двумя буквами, поставленными у концов его, либо одной строчной буквой у его середины.

ПРЯМЫЕ ПАРАЛЛЕЛЬНЫЕ. 1. Две прямые, лежащие в одной плоскости и не имеющие общих точек. Через данную точку, взятую вне прямой, можно провести только одну прямую, параллельную этой прямой. Одноименные проекции двух параллельных линий параллельны между собой. 2. Прямые, пересекающиеся в бесконечно удаленной точке.

ПРЯМЫЕ ПЕРЕСЕКАЮЩИЕСЯ. Две прямые, имеющие единственную общую точку. Точки пересечения их одноименных проекций лежат на линии проекционной связи (на одном перпендикуляре к оси проекций).

ПРЯМЫЕ СКРЕЩИВАЮЩИЕСЯ. Две прямые, которые не параллельны друг другу и не пересекаются. Такие прямые лежат в различных плоскостях. Расстояние между двумя скрещивающимися прямыми равно длине отрезка перпендикуляра, опущенного из точки на одной прямой на другую прямую; существует только один такой перпендикуляр, общий этим прямым. Углом двух скрещивающихся прямых условно считают острый угол, построенный в произвольно выбранной точке со сторонами, соответственно параллельными этим прямым.

ПЛОСКОСТЬ следует рассматривать как частный случай поверхности. Это двумерный геометрический образ. Плоскость считается бесконечной, не имеющей толщины и непрозрачной.

ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ. Плоскость, расположенная наклонно ко всем плоскостям проекций.

ПЛОСКОСТЬ УРОВНЯ. В начертательной геометрии – плоскость, параллельная какой-либо плоскости проекций. В стереометрии – плоскость, параллельная основной плоскости.

ПЛОСКОСТЬ ПРОЕЦИРУЮЩАЯ. Плоскость, перпендикулярная какой-либо плоскости проекций.

ПРЯМАЯ ЛИНИЯ – одномерный геометрический образ, имеющий только длину. Прямая – бесконечная линия.

ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ. Прямая, расположенная наклонно ко всем плоскостям проекций. Отрезок такой прямой проецируется на плоскости проекций с искажением; все проекции плоскости меньше натуральной величины.

ПРЯМАЯ УРОВНЯ. Прямая, параллельная какой-либо плоскости проекций.

ПРЯМАЯ ЧАСТНОГО ПОЛОЖЕНИЯ. Прямая, расположенная в пространстве, параллельная или перпендикулярная какой-либо плоскости проекций. Если такая прямая перпендикулярна к одной плоскости проекций, то она одновременно параллельна двум другим. Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной (горизонталь). Прямая, параллельная фронтальной плоскости проекций, называется фронтальной (фронталь). Прямая, параллельная профильной плоскости проекций, называется профильной (профиль).

ПРЯМЫЕ ПРОЕЦИРУЮЩИЕ. Прямые, перпендикулярные к плоскостям проекций. Прямая, перпендикулярная к горизонтальной плоскости проекций, называется горизонтально проецирующей. Прямая, перпендикулярная к фронтальной плоскости проекций, называется фронтально проецирующей. Прямая, перпендикулярная к профильной плоскости проекций называется профильно проецирующей.

ТОЧКА. Одно из основных понятий геометрии. Простейший неделимый элемент геометрического пространства. Несколько древне-классических определений: 1. Точка есть то, то не имеет частей (Эвклид); 2. Концы линий суть точки (Эвклид); 3. То, что не имеет частей, но имеет положение (Аристотель). На чертеже мы имеем не геометрическую точку, а ее изображение (образ), которое обладает некоторыми малыми размерами. Это изображение мы условно называем точкой и локально определяем как место пересечения двух линий.

ТОЧКИ КОНКУРИРУЮЩИЕ. Две точки А и В, расположенные на одном проецирующем луче, имеют общую проекцию, обозначаемую на чертеже двумя буквами Аp Вp. Такая надпись (сначала видимая точка, затем невидимая) означает, что точка А в пространстве дальше отстоит от плоскости проекций, чем точка В. Точки, имеющие общую проекцию, названы конкурирующими профессором Д.Г. Анановым.

ФРОНТАЛЬ ПЛОСКОСТИ. Прямая, принадлежащая данной плоскости и параллельная фронтальной плоскости проекций.