Две плоскости будут перпендикулярны друг к другу, если одна из них проходит через прямую, перпендикулярную другой плоскости (рис. 6.4).
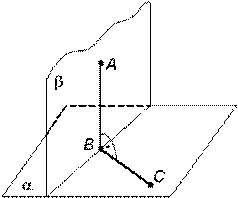
Рис 6.4
АВ 
b, то есть АВ принадлежит плоскости b и АВ ^ плоскости a. Плоскость b ^ плоскости a.
Рассмотрим это положение на комплексном чертеже (табл. 6.7), где будет показано построение плоскости Р, проходящей через прямую l и перпендикулярной плоскости, заданной треугольником Q(D АВС) (табл. 6.7).
Таблица 6.7
Алгоритм построения плоскости, перпендикулярной данной
| Вербальная форма | Графическая форма |
| 1. Известно, что для построения прямой, перпендикулярной плоскости, необходимо построить горизонталь и фронталь в плоскости. а) Заметим, что построение перпендикуляра упрощается, так как стороны плоскости Q(D АВС) являются прямыми уровня: АВ (А1В1; А2В2) – фронталь АС (А1С1; А2С2) – горизонталь. б) Возьмем на прямой l произвольную точку К |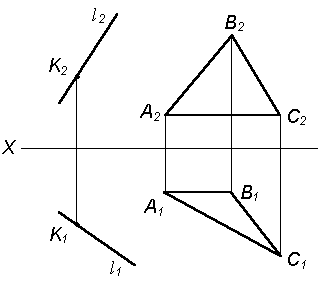 
|
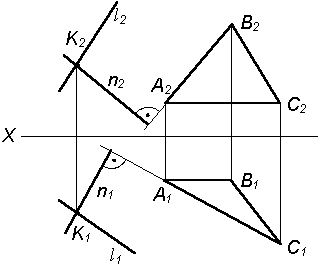
2. Через точку К, которая принадлежит прямой l, проводим прямую n ^ Q, т.е.
n1^ A1C1 и n2^ A2В2.
Искомая плоскость будет определяться двумя пересекающимися прямыми, одна из которых задана – l, а другая – n является перпендикулярной к заданной плоскости:
P(l  n)^ Q (D ABC)
| 
|
Выводы
1. Прямая и плоскость в пространстве могут:
а) не иметь общих точек;
б) иметь хотя бы одну общую точку;
в) иметь множество общих точек.
В зависимости от этого прямая может принадлежать плоскости, быть ей параллельна, пересекаться с данной плоскостью и, как частный случай, быть ей перпендикулярна.
2. Две плоскости в пространстве могут быть параллельны друг другу, пересекаться между собой и, как частный случай, быть взаимно перпендикулярны.
3. Две пересекающиеся плоскости имеют одну общую прямую – линию пересечения.
4. Прямая, пересекающая плоскость, имеет с ней одну общую точку.
5. Для построения перпендикуляра к плоскости необходимо использовать свойства проецирования прямого угла.
Вопросы для самоанализа
1. Назовите признаки параллельности прямой и плоскости, двух плоскостей.
2. Какая прямая является линией пересечения плоскости общего положения с фронтально проецирующей плоскостью?
3. По какой линии пересекаются две горизонтально проецирующие плоскости?
4. Как определяется видимость при пересечении двух плоскостей, прямой и плоскости?
5. Какова последовательность построения точки пересечения прямой и плоскости?
6. Как провести плоскость, перпендикулярную данной прямой (через точку на прямой или через точку вне прямой)?
7. Как провести перпендикуляр к прямой общего положения?
8. Как через прямую провести плоскость, перпендикулярную данной плоскости?
Основные понятия, которые необходимо знать:
– признаки параллельности и перпендикулярности прямой и плоскости двух плоскостей;
– принадлежность прямой двум плоскостям одновременно;
– принадлежность точки прямой и плоскости.
Способы деятельности, которыми необходимо владеть:
– построение линии пересечения двух плоскостей;
– построение точки пересечения прямой и плоскости;
– определение видимости прямой и плоскости относительно плоскостей проекций;
– построение прямой, параллельной плоскости;
– построение прямой, перпендикулярной плоскости;
– построение плоскости, перпендикулярной или параллельной данной плоскости.
