Образование комплексного чертежа (эпюра)

Для удобства пользования полученными изображениями от пространственной системы плоскостей перейдем к плоскостной.

Для этого:

1. Применим способ вращения плоскости p₁ вокруг оси Х до совмещения с плоскостью p₂ (рис. 2.7)

2. Совмещаем плоскости p₁ и p₂ в одну плоскость чертежа (рис. 2.8)

Рис. 2.7	Рис. 2.8

Проекции А₁ и А₂ располагаются на одной линии связи перпендикулярной оси Х. Эта линия называется линией проекционной связи (рис. 2.9).

Рис. 2.9

Так как плоскость проекций считается бесконечной в пространстве, то границы плоскости p₁, p₂ можно не изображать (рис. 2.10).

Рис. 2.10

В результате совмещения плоскостей p₁ и p₂ получается комплексный чертеж или эпюр (от франц. epure чертеж), т.е. чертеж в системе p₁ и p₂ или в системе двух плоскостей проекций. Заменив наглядное изображение эпюром, мы утратили пространственную картину расположения плоскостей проекций и точки. Но эпюр обеспечивает точность и удобоизмеряемость изображений при значительной простоте построений. Чтобы представить по эпюру пространственную картину, требуется работа воображения: например, по рис. 2.11 надо представить картину, изображенную на рис. 2.12.

При наличии на комплексном чертеже оси проекций по проекциям А₁ и А₂ можно установить положение точки А относительно p₁ и p₂ (см. рис. 2.5 и 2.6). Сравнивая рис. 2.11 и 2.12 нетрудно установить, что отрезок А₂ А_Х – расстояние от точки А до плоскости p₁, а отрезок А₁А_Х – расстояние от точки А до p₂. Расположение А₂ выше оси проекций означает, что точка А расположена над плоскостью p₁. Если А₁ на эпюре расположена ниже оси проекций, то точка А находится перед плоскостью p₂. Таким образом, горизонтальная проекция геометрического образа определяет его положение относительно фронтальной плоскости проекций p₂, а фронтальная проекция геометрического образа – относительно горизонтальной плоскости проекций p₁.

Рис. 2.11	Рис. 2.12

 

§ 4. Характеристика положения точки в системе p ₁ и p ₂

Точка, заданная в пространстве, может иметь различные положения относительно плоскостей проекций (рис. 2.13).

Рис. 2.13

Рассмотрим возможные варианты расположения точки в пространстве первой четверти:

1. Точка расположена в пространстве I четверти на любом расстоянии от оси Х и плоскостей p _{1p 2}, например точки А, В (такие точки называются точками общего положения) (рис. 2.14 и рис. 2.15).

Рис. 2.14	Рис. 2.15

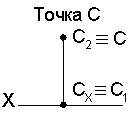
2. Точка С принадлежит плоскости p₂, точка D – плоскости p₁ (рис. 2.16 и рис. 2.17)

Рис. 2.16	Рис. 2.17

3. Точка K принадлежит одновременно и плоскости p₁ и p₂, то есть принадлежит оси Х (рис. 2.18):

Рис. 2.18

На основании вышеизложенного можно сделать следующий вывод:

1. Если точка расположена в пространстве I четверти, то ее проекция А₂ расположена выше оси Х, а А₁ – ниже оси Х; А₂А₁ – лежат на одном перпендикуляре (линии связи) к оси Х (рис. 2.14).

2. Если точка принадлежит плоскости p₂, то ее проекция С₂ С (совпадает с самой точкой С) а проекция С₁ Х (принадлежит оси Х) и совпадает с С_Х: С₁ С_Х.

3. Если точка принадлежит плоскости p₁, то ее проекция D₁ на эту плоскость совпадает с самой точкой D D_1, а проекция D₂ принадлежит оси Х и совпадает с D_Х: D₂ D_Х.

4. Если точка принадлежит оси Х, то все ее проекции совпадают и принадлежат оси Х: К К₁ К₂ К_Х.

Задание:

1. Дать характеристику положения точек в пространстве I четверти (рис. 2.19).

Рис. 2.19

2. Построить наглядное изображение и комплексный чертеж точки по описанию:

а) точка С расположена в I четверти, и равноудалена от плоскостей p₁ и p₂.

б) точка М принадлежит плоскости p₂.

в) точка К расположена в первой четверти, и ее расстояние до p₁ в два раза больше, чем до плоскости p₂.

г) точка L принадлежит оси Х.

3. Построить комплексный чертеж точки по описанию:

а) точка Р расположена в I четверти, и ее расстояние от плоскости p₂ больше, чем от плоскости p₁.

б) точка А расположена в I четверти и ее расстояние до плоскости p₁ в 3 раза больше, чем до плоскости p₂.

в) точка B расположена в I четверти, и ее расстояние до плоскости p₁=0.

4. Сравнить положение точек относительно плоскостей проекций p₁ и p₂ и между собой. Сравнение ведется по характеристикам или признакам. Для точек эти характеристики есть расстояние до плоскостей p₁; p₂ (рис. 2.20).

Рис. 2.20

Применение вышеизложенной теории при построении изображений точки может быть осуществлено различными способами:

• словами (вербальное);
• графически (чертежи);
• наглядное изображение (объемное);
• плоскостное (комплексный чертеж).

Умение переводить информацию с одного способа на другой способствует развитию пространственного мышления, т.е. с вербального в наглядное (объемное), а затем в плоскостное, и наоборот.

Рассмотрим это на примерах (табл. 2.1 и табл. 2.2).

Таблица 2.1

Пример изображения точек
в системе двух плоскостей проекций

Четверть пространства	Наглядное изображение	Комплексный чертеж	Характерные признаки
I			Фронтальная проекция точки А выше оси Х, горизонтальная проекция точки А ниже оси X
II			Фронтальная и горизонтальная проекции точки B выше оси Х
III			Фронтальная проекция точки С ниже оси Х, горизонтальная проекция точки C выше оси X
IV			Фронтальная и горизонтальная проекции точки D ниже оси Х

Таблица 2.2

Пример изображения точек, принадлежащих плоскостям p ₁ и p ₂

Положение точки	Наглядное изображение	Комплексный чертеж	Характерные признаки
Точка А принадлежит плоскости p 1			А1 – ниже оси Х, А2 – на оси X
Точка B принадлежит плоскости p 1			B1 – выше оси X, B2 – на оси X
Точка С принадлежит плоскости p 2			С2 – выше оси X, С1 – на оси Х
Точка D принадлежит плоскости p 2			D1 – на оси X, D2 – ниже оси X
Точка Е принадлежит оси X			E1 совпадает с E2 и принадлежит оси X

Задача № 1.

Построить комплексный чертеж точки А, если:

1. точка расположена во II четверти и равноудалена от плоскостей p₁ и p₂.

2. точка расположена в III четверти, и ее расстояние до плоскости p₁ в два раза больше, чем до плоскости p_2.

3. точка расположена в IV четверти, и ее расстояние до плоскости p₁ больше, чем до плоскости p₂.

Задача № 2.

Определить, в каких четвертях расположены точки (рис. 2.21).

Рис. 2.21

Задача № 3.

1. Построить наглядное изображение точек в четвертях:

а) А – общего положения в III четверти;

б) В – общего положения в IV четверти;

в) С – во второй четверти, если ее расстояние от p₁ равно 0;

г) D – в I четверти, если ее расстояние от p₂ равно 0.

Задача № 4.

Построить комплексный чертеж точек А, В, С, D (см. задачу 3).