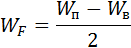Для работы электронных приборов необходимы свободные электроны. Для определения вероятности события, что некоторый электрон занимает определенный энергетический уровень необходимо воспользоваться функцией распределения Ферми-Дирака:
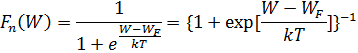
Оно применимо к частицам, волновые функции которых подчиняются запрету Паули.
Где Fn(W) – вероятность того, что заданный энергетический уровень W при заданной температуре T будет занят электроном.
кT – средняя тепловая энергия электрона.
к – постоянная Больцмана (1,38*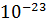 
).
– химический потенциал системы, имеющий размерность энергии и называется уровнем Ферми.
Частицы, подчиняющиеся этой статистике, называются фермионами.
Исследуем свойства функции Fn(W).
Можно показать, что уровень Ферми представляет собой некоторую функцию температуры (T), действительно:
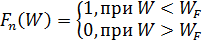
Если W<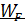 
, W- <0, или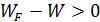 
, т.е.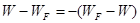 
Тогда Fn(W) =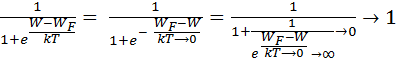 
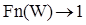
Если W> 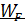, то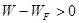 
Тогда Fn(W)=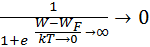 
; 
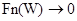
Практически независимо от температуры, при W= функция Fn(W) будет:
Fn(W)=1/2
Таким образом, уровень Ферми можно определить как уровень, вероятность заполнения которого равна 0,5 при Т≠0, что может быть представлено графически следующим образом:
Значения при Т=0К представляет собой то максимально допустимое значение энергии, ниже которого все энергетические уровни заняты (т.к. Fn(W)=1), а выше которого все уровни пусты (т.к. Fn(W)=0).
Функция Fn(W) показывает, что вероятность занятия уровня энергии при повышении температуры растет, а при - понижении падает.
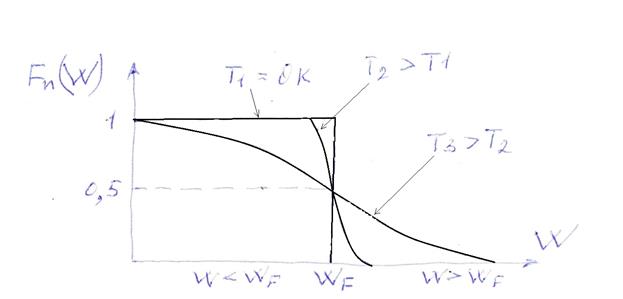
Вероятность события, что некоторый энергетический уровень Fn(W) занят не электроном, а дыркой равна:
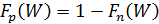
При изучении явлений, связанных с дырками, часто полагают, что:
W<< и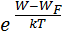 
<<1, поэтому:
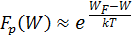- распределение Максвелла-Больцмана.
Из анализа функций распределения следует, что уровень Ферми должен располагаться в середине запрещенной зоны.
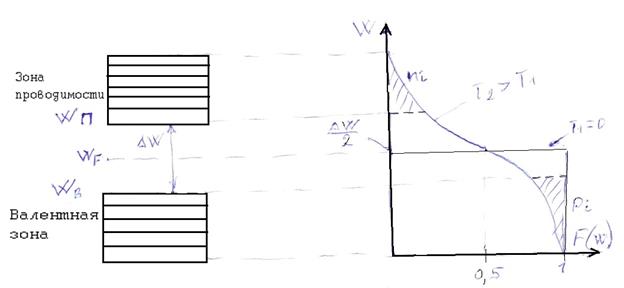
На рисунке показана энергетическая диаграмма собственного (беспримесного) полупроводника (ni=pi), а также график зависимости распределения подвижных носителей зарядов по энергиям при различных температурах. При Т1=0К валентная зона заполнена полностью [F(W)=1], а зона проводимости пуста [F(W)=0]. Уровень Ферми в этом случае совпадает с максимальной энергией, которую может иметь электрон при Т=0К.
С повышением температуры Т2>Т1 начинается термогенерация электронно-дырочных пар и возникает вероятность появления свободных электронов ni в зоне проводимости и дырок pi в валентной зоне.
Концентрация электронов и дырок пропорциональна заштрихованным площадкам.
Отсюда следует, что в собственном полупроводнике уровень Ферми располагается в середине запрещенной зоны и его энергия определяется:
