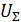= 
Если к p-n переходу подключить внешнее Евн напряжение, полярность которого совпадает с полярностью контактной разности Uк потенциалов, то такое включение называется обратным (n-область подключается к положительному полюсу Евн, а p-область к отрицательному полюсу Евн). При таком включении в p-n переходе появится дополнительное внешнее электрическое поле, увеличивающее его внутреннее поле. Суммарное поле Еε, действующее в переходе, будет определяться:
=
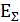Это поле увеличит тормозящее действие на основные носители заряда и их движение уменьшится, а при некотором значении Евн совсем прекратится и ток диффузии станет равным нулю (Iдиф=0).
Под действием электрического поля Евн основные носители заряда будут оттягиваться от пограничных слоев p-n перехода, увеличивая дефицит свободных носителей в области перехода и расширяя переход (увеличение его толщины).
Для неосновных носителей заряда Евн является ускоряющим полем, поэтому оно будет поддерживать дрейфовый ток, переводя неосновные носители через расширенный p-n переход.
Процесс перевода (оттягивания, «отсоса») носителей заряда через p-n переход из областей, где они становятся основными носителями, под действием обратного напряжения на переходе, называется экстракцией.
При малых значениях обратного напряжения на переходе навстречу дрейфовому току протекает диффузионный ток (I0=Iдиф), который уменьшается по экспоненциальному закону:
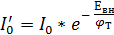
Результирующий ток через p-n переход в этом случае будет называться обратным током и определяется:
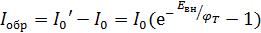
Поскольку φт =26 мВ при Т=300 К, то уже при |Евн|>3φт током основных носителей можно пренебречь, и обратный ток будет определяться током I0, независящим от Евн. Поэтому I0 в этом случае называют обратным током насыщения или просто обратным током. (Он зависит от температуры и от концентрации носителей в собственном полупроводнике)
Эмпирическим путем установлено, что значение тока в зависимости от температуры может быть выражено:
,
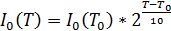Где Т – текущая температура,
Т0 - температура, при которой значения тока I0 известно.
Эта формула носит название формулы «удвоения». Эта формула имеет более высокую точность для полупроводников на основе германия и меньшую точность – для кремния.
Диаграмма энергетических зон p-n перехода при обратном смещении
При подаче обратного напряжения на p-n переход (Евн < 0), Uк и Евн суммируются, что ведет к расширению обедненной области.
Различие свойств при прямом и обратном напряжении определяет возможность его работы в качестве выпрямляющего элемента.
Уравнение Шокли.
Анализ выражений для токов через p-n переход при прямых и обратных напряжениях позволяет установить аналитическую зависимость:
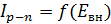
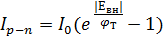
Это уравнение называется уравнением диода или уравнением Шокли, где I0 – тепловой ток или обратный ток насыщения.
Термин «тепловой» отражает сильную температурную зависимость I0 от температуры, а также тот факт, что I0 = 0 при Т = 0 К.
Термин «обратный ток насыщения» отражает тот факт, что при отрицательном напряжении Евн и |Евн|>>φт, обратный ток идеализированного диода равен (-I0) и не зависит от Евн.
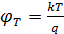, где k = 1,38* 
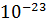Дж/К – постоянная Больцмана;
q = 1,6*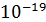 
Кл;
Т – абсолютная температура;
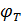=26 БмВ при Т = 300 К.
Действительно,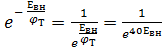 
близко к нулю.
Это значит, что при обратном включении Ip-n(обр) = -I0 и не зависит от величины обратного напряжения.
Вольт-амперная характеристика(ВАХ)
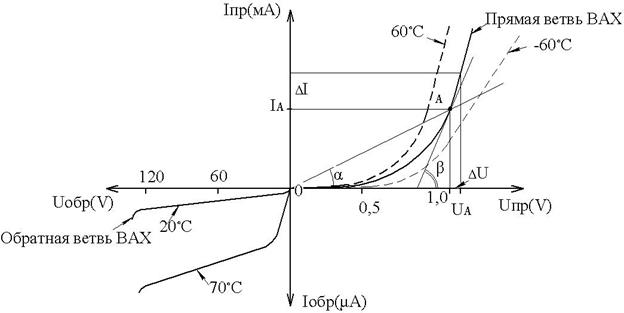p-n перехода
Статическое сопротивление p-n перехода в рабочей точке (А) определяется как отношение напряжения в этой точке к току, соответствующему этому напряжению или равно ctgα – угла образованного прямой, проходящей через начало координат и рабочую точку(А) и осью абсцисс(Х).
Дифференциальное сопротивление p-n перехода в рабочей точке(А) определяется как отношение приращения напряжения в этой точке к приращению тока, соответствующего этому приращению напряжения
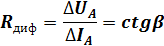
или равно ctgβ – угла образованного касательной к этой точке и осью абсцисс.
Реальная ветвь(прямая) ВАХ перехода отклоняется от идеальной ВАХ в основном за счёт падения напряжения на сопротивлении базы(rБ), с учётом этого уравнение перехода может быть определено:
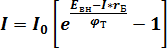
Прологарифмировав это выражение можно определить падение напряжения на переходе при прямом включении.
Заменив Eвн на Uпр, получим:
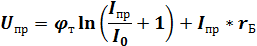
Для малых токов Iпр имеем:
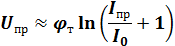
Статическое и дифференциальное сопротивление для обратной ветви ВАХ рассчитывается аналогично прямой ветви ВАХ
Rст.пр ≪ Rст.обр.;
Rдиф.пр ≪ Rдиф.обр.; при Uпр.= |Uобр.|>U, |Uобр.|<Uпроб.
Пробой p-n перехода
Несмотря на то, что в определённых пределах отсутствует зависимость величины обратного тока p-n перехода от величины приложенного обратного напряжения, может наступить момент, когда эта зависимость начнёт проявляться.
Из уравнения Шокли следует, что при увеличении обратного напряжения на p-n переходе Iобр стремится к I0. Использовать эту формулу при больших значениях обратного напряжения нецелесообразно, так как она перестаёт соответствовать явлениям, происходящим в реальных p-n переходах. На практика Iобр незначительно возрастает, пока напряжение на переходе не достигнет некоторого критического значения, называемого напряжением пробоя (Uпрб). После этого Iобр возрастает скачкообразно, как это показано на графике:
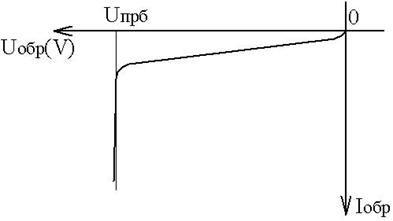
Таким образом, под пробоем p-n перехода понимают явление значительного уменьшения дифференциального сопротивления Rдиф (и Rст – тоже) и увеличение Iобр при увеличении обратного напряжения Uобр.
Различают три вида пробоя:
1) – тепловой;
2) – лавинный;
3) – туннельный.
На практике встречаются и смешанные случаи, т.к. один вид пробоя может наступить как следствие другого вида пробоя.
Тепловой пробой, как явление, в основном носит необратимый характер и приводит к разрушению p-n перехода.
Лавинный и туннельный виды пробоя являются электрическим или полевым видом пробоя, который обеспечивает обратимость при ограничении мощности на p-n переходе (p-n переход не разрушается).
