Рис. 2.12 Рис. 2.13
Используя уравнение Клапейрона pv = RT, можно получить соотношения между другими параметрами в адиабатном процессе:
, (2.45)
. (2.46)
Переписав уравнение (2.45) в виде 
и учитывая, что точки 1 и 2 выбраны произвольно, приходим к выводу, что выражение
(2.47)
обладает общностью и справедливо для любой точки процесса, поэтому может служить уравнением адиабатного процесса. Его использование удобно для анализа адиабаты в р, v-диаграмме.
Реже применяется уравнение адиабаты, полученное из формулы (2.45) и (2.46), в виде 
или 
.
В диаграмме р,v адиабата, как видно из уравнения (2.47), представляет собой неравнобокую гиперболу (рис. 2.13). Здесь же показана изотерма
pv = const. Сравним конечные давления в одинаковых интервалах изменения объема соответственно для адиабаты и изотермы, исходящих из точки 1:
p2 = p1 (v1/v2)k; p2' = p1 (v1/v2).
Так как 
> 1, a v1 / v2 < 1, то (v1 / v2) k < v1 / v2, т. е. p2 < p2'. Таким образом, адиабата проходит в р,v-диаграмме более круто, чем изотерма.
Работа адиабатного процесса на основании первого закона термодинамики dq = du + dl при dq = 0
dl = – du, (2.48)
т.е. работа совершается за счет убыли внутренней энергии. Поскольку для любого процесса с идеальным газом du = cvdT, то dl = – cvdT или в конечном процессе 1 – 2
l1–2 = cv(T1 – T2) = – ∆u1 – 2. (2.49)
С учетом выражений (2.43), (2.46) и уравнения Клапейрона можно записать еще несколько удобных для работы выражений через различные
параметры:
. (2.50)
Политропный процесс носит обобщающий характер, так как здесь не накладывается какого-либо ограничения, например постоянства одного из параметров в изохорном, изобарном и изотермном процессах или отсутствия теплообмена в адиабатном процессе. В связи с этим уравнение политропного процесса должно быть выведено из наиболее общих предпосылок. Воспользуемся для этого уравнением первого закона термодинамики, которое для идеального газа можно записать в виде: dq = cvdT + pdv.
Элементарное количество тепла dq можно выразить через произведение теплоемкости политропного процесса с на приращение температуры dT, тогда cdT = cvdT + pdv или
(cv – c)dT+ pdv = 0. (2.51)
Дифференцируя уравнение Клапейрона pdv + vdp = RdT, имеем
. (2.52)
Совместное решение уравнений (2.51) и (2.52) приводит к выражению:
.
Введя обозначение
(2.53)
и разделяя переменные, имеем n = (dv/v) + dp/p = 0, откуда после интегрирования получаем уравнение политропного процесса:
. (2.54)
Величина n называется показателем политропного процесса. Как и показатель адиабаты k = cp / cv, показатель политропы n, согласно выражению (2.53), представляет собой отношение теплоемкостей.
Конструктивно уравнение политропы аналогично уравнению адиабаты. На этом основании можно заключить, что все зависимости, вытекающие из этих уравнений, будут иметь внешнее сходство, только вместо k следует ставить n.
В соответствии с формулами (2.52) – (2.54) соотношения параметров в политропным процессе имеют вид:
(2.55)
Работа политропного процесса, согласно выражению (2.50),
. (2.56)
Количество тепла в политропном процессе
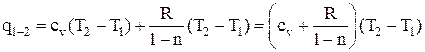. (2.57)
В то же время q1–2 = c (T2 – T1), поэтому теплоемкость политропного процесса
c = cv + R / (1 – n). (2.58)
К выражению (2.58) можно было прийти и непосредственно из уравнения (2.53). Подстановкой R = cp – cv и = cp / cv выражение (2.58) приводится
к виду:
, (2.59)
более удобному для анализа зависимости c от n.
Одновременно проследим, как уравнение политропы трансформируется в соответствующие уравнения для частных (рассмотренных ранее) процессов.
Принимая n = , находим, что теплоемкость такого процесса с = 0. Этот случай характерен для адиабаты, где dq = 0, с = dq / dT = 0. Подставив в уравнение политропы вместо n показатель k, получаем уравнение адиабаты: .
При n =1 с = ∞, что свойственно изотерме, dT = 0, c = dq / dT = ± ∞. Уравнение политропы pvn = const при n = 1 становится уравнением изотермы:
рv = const. При n = 0 с = cv = cp, т. е. теплоемкость становится изобарной, уравнение политропы приобретает вид: р = const.
При n = ± ∞, представив выражение (2.59) в виде
, (2.60)
имеем с = cv. Уравнение политропы, переписанное в виде p1/ n v = const, переходит в уравнение изохоры: v = const.
Таким образом, политропный процесс, описываемый уравнением
pvn = const, обобщает все частные случаи, при этом показатель политропы n и теплоемкость c принимают конкретные, вполне определенные значения.
Характер зависимостей теплоемкости с от показателя политропы n показан на рис. 2.14. Интересно отметить, что теплоемкость с, как видно из уравнения (2.59) и рис. 2.14, при 1 < n < k отрицательна. В этих процессах газ за счет внутренней энергии производит работу, превышающую количество подведенного тепла. Убыль внутренней энергии ведет к снижению температуры, хотя тепло подводится.
Практическое использование формул для политропного процесса возможно в том случае, если известен показатель политропы n.
При заданных начальных и конечных параметрах процесса величина n определяется из следующих соображений.
Логарифмируя уравнение политропы 
, получаем
. (2.61)
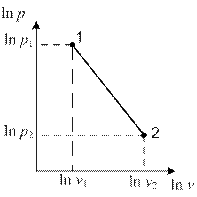
Построив точки 1 и 2 в логарифмической диаграмме р,v (рис.2.15), обнаруживаем, что показатель n равен тангенсу угла наклона линии 1 – 2.
При переменном показателе политропы найденная величина n является средним значением показателя политропы в процессе 1 – 2. В том случае, когда по опытным данным можно построить график процесса (рис. 2.16), истинное значение n в каждой точке процесса определяется следующим образом.
В произвольной точке M 
, отсюда
. (2.62)
Дифференцируя уравнение политропы (2.54) vnpd + npvn–1dv = 0 и разделив его на vn–1, имеем vpd + npdv = 0 или
. (2.63)
Ошибка! Ошибка связи.
Рис. 2.15 Рис. 2.16
Сравнивая (2.62) и (2.63), получаем ā = v / n, n = v / ā. Для любой точки процесса в р, v-диаграмме показатель политропы есть отношение величины удельного объема в этой точке к величине отрезка подкасательной.
На рис. 2.17, 2.18 в р,v- и Т, s-диаграммах показано относительное расположение изохоры, изобары, изотермы и адиабаты, проведенных через произвольную точку О. При этом поле диаграммы разделяется на восемь областей, в которых показатель политропы n принимает различные значения, изменяясь по величине и по знаку. В областях 1 и 5 0 > n > – ∞, в областях 2 и 6 1 > n > 0, в областях 3 и 7 k > n > 1, в областях 4 и 8 +∞ > n > k.
Так как dq = Tds, то все процессы, начинающиеся в точке О и проходящие в областях 8, 1, 2, 3, т. е. протекающие при возрастании энтропии, будут идти с подводом тепла: dq > 0. В областях же 4, 5, 6, 7 dq < 0.
Знак изменения внутренней энергии определяется изменением температуры в процессе: du = cvdT. Поэтому в областях 7, 8, 1, 2 du > 0, а в областях 3, 4, 5, 6 du < 0.
Считая работу расширения положительной, а сжатия – отрицательной
(dl = pdv), устанавливаем, что в областях 1, 2, 3, 4, где процессы протекают с ростом удельного объема, dl > 0, а в областях 5, 6, 7, 8 dl < 0.
Всю эту информацию о знаке тепла, изменения внутренней энергии и работы в различных процессах сведем в табл. 2.1.
В заключение приведем сводку формул по газовым процессам, которая весьма удобна при решении практических задач, а также для подготовки к экзаменам.
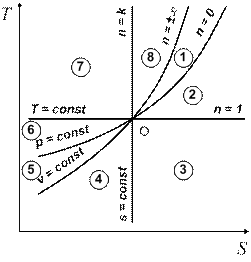
Рис. 2.17 Рис. 2.18
Таблица 2.1
Определение знака тепла, внутренней энергии и работы
| Величина | Область диаграммы | |||||||
| q1–2 | + | + | + | – | – | – | – | + |
| ∆u1–2 | + | + | – | – | – | – | + | + |
| l1–2 | + | + | + | + | – | – | – | – |
