На высоких частотах плотность тока изменяется по сечению проводника. Она максимальна на поверхности и убывает по мере проникновения вглубь проводника. Это явление называется поверхностным эффектом.
Неравномерное распределение тока объясняется действием магнитного поля тока, протекающего по проводнику. Магнитный поток, сцепленный с проводом, пропорционален току:
Φ = L*i,
где L — индуктивность проводника.
Если ток изменяется по синусоидальному закону i = I m*sin(
), то изменение магнитного потока вызывает появление ЭДС самоиндукции:
Эта ЭДС имеет направление, противоположное току в проводе, и тормозит его изменение в соответствии с законом Ленца.
При прохождении переменного тока переменное магнитное поле возникает как вокруг проводника, так и внутри него. При этом потокосцепление максимально для внутренних слоев и минимально для внешних слоев. Поэтому ЭДС самоиндукции оказывается максимальной в центре проводника и уменьшается в направлении к поверхности. Соответственно, и плотность тока наиболее значительно ослабляется в центральной части проводника и в меньшей степени — у поверхности, иначе говоря, происходит вытеснение тока к поверхности проводника. Оно тем сильнее, чем выше частота.
Распределение плотности тока по сечению проводника подчиняется экспоненциальному закону:
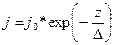
где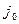 
— плотность тока на поверхности;
z — расстояние, измеряемое от поверхности;
Δ — глубина проникновения тока.
Глубина проникновения тока, выраженная в миллиметрах, равна расстоянию, на котором плотность тока уменьшается в е = 2,72 раз по отношению к своему значению на поверхности проводника. Она пропорциональна удельному сопротивлению ρ [Ом-м] и обратно пропорциональна частоте f [МГц]:
В случае сильно выраженного поверхностного эффекта, когда ток протекает по тонкому поверхностному слою, толщина которого много меньше диаметра провода d, экспоненциальное распределение тока может быть заменено однородным распределением с постоянной плотностью тока в пределах тонкого слоя толщиной Δ, на основании чего можно ввести понятие эквивалентной площади сечения проводника, занятой током:
Поскольку площадь сечения, через которое протекает ток, уменьшилась, то сопротивление провода переменному току R~ стало больше, чем его сопротивление постоянному току Ro, что учитывают коэффициентом увеличения сопротивления:
Полученная формула справедлива при Δ << d.
