Роль математики в общечеловеческой культуре огромна. Обращаясь к истории философии, следует отметить, что ученые, создававшие математику Нового времени, рассматривали математическую науку как составную часть философии, которая служила средством познания мира (рисунок 1).
Место математики в жизни и в науке определяется тем, что она позволяет перевести «общежитейские», интуитивные подходы к действительности, базирующиеся на приблизительных описаниях, на язык точных определений и формул, из которых возможны количественные выводы. Не случайно говорят, что степень научности той или иной дисциплины измеряется тем, насколько в ней применяется математика.
Рисунок 1
Математика является частью общечеловеческой культуры. На протяжении нескольких тысячелетий развития человечества шло накопление математических фактов, что привело около двух с половиной тысяч лет назад к возникновению математики как науки. Квадривий, изучавшийся в Древней Греции, включал арифметику, геометрию, астрономию и музыку. О значении математики для человечества говорит тот факт, что «Начала» Евклида издавались бесчисленное число раз (не считая Библии).
Математика способствует выработке научного мировоззрения и достижению необходимого общекультурного уровня. История зарождения великих математических идей, судьбы выдающихся математиков (Архимед, Галуа, Паскаль, Галилей, Гаусс, Эйлер, Ковалевская, Чебышев и др.) дают пищу для ума и сердца, примеры беззаветного служения науке, приводят к философским размышлениям и нравственным поискам.
Математические рассуждения позволяют правильно устанавливать причинно-следственные связи, что, безусловно, должен уметь каждый человек. Стиль изложения математики, ее язык влияют на речь. Каждый культурный человек должен иметь представление об основных понятиях математики, таких, как число, функция, математическая модель, алгоритм, вероятность, оптимизация, величины дискретные и непрерывные, бесконечно малые и бесконечно большие. Речь идет именно об основных понятиях и идеях, а не о наборе конкретных формул и теорем.
Человек, знающий математику лишь по школьному курсу, вряд ли сознает, сколь мизерное (но предельно необходимое) количество знаний, накопленных задолго до начала XX в., сообщается в школе. А ведь в наши дни в мире ежемесячно выходят сотни математических журналов, публикующих тысячи новых теорем с трудными, порой многостраничными доказательствами. И это не считая публикаций по приложениям математики. Следует отметить тесную взаимосвязь между расширением ее фронта, усилением активности и изменением представлений математиков о предмете своей науки (хотя полного единодушия во взглядах нет).
Сейчас не удивишь словосочетаниями «математическая лингвистика», «математическая биология», «математическая экономика» и т.п. Какую дисциплину ни взять, вряд ли кому-нибудь покажется невозможным присоединение к ее наименованию эпитета «математический». Математика занимает сегодня видное место в жизни общества.
Тем не менее, повсеместный триумф математики некоторым кажется загадочным, даже подозрительным. Не вызывает сомнений право на всеобщее признание, например, физики или химии. Физика открывает нам новые источники энергии, новые средства быстрой связи. Химия создает искусственные ткани, сейчас пытается создать искусственную пищу. Неудивительно, что эти науки, помогающие человеку в его извечных поисках энергии, связи, одежды и еды, прочно вошли в нашу жизнь.
Что же дает математика, которая не открывает новых способов передвижения, как физика, и не создает новых вещей, как химия? Почему появление в какой-либо отрасли науки и техники математических методов означает и достижение в этой отрасли определенного уровня зрелости, и начало нового этапа развития?
Еще недавно ответ на эти вопросы состоял в том, что математики умеют хорошо вычислять и осуществляют математическую обработку цифровых данных, связанных с тем или иным изучаемым процессом. Однако при всей важности вычислительного аспекта математики, особенно в последние годы в связи с бурным ростом вычислительной техники, он оказывается неглавным при попытке объяснить причины математизации современного мира.
Главная причина этого процесса такова: математика предлагает весьма эффективные модели для изучения окружающей действительности в отличие от менее общих и более расплывчатых моделей, предлагаемых другими науками. Такие модели математика дает с помощью своего особого языка – языка чисел, различных символов. При этом математическая модель, отображая и воспроизводя те или иные стороны рассматриваемого объекта, способна замещать его так, что исследование модели даст новую информацию об объекте, опирающуюся на принципы математической теории, сформулированные математическим языком законы природы и общества. Если математическая модель верно отражает суть данного явления, то она позволяет находить и не обнаруженные ранее закономерности, давать математический анализ условий, при которых возможно решение теоретических или практических задач, возникающих при исследовании этого явления.
Возникает один общий вопрос: нужна ли математика гуманитарию вообще?
Известно, что математика является частью общечеловеческой культуры, такой же неотъемлемой и важной, как право, медицина, естествознание и многое другое. Все лучшие достижения человеческой мысли, человеческих рук и составляют основу гуманитарного образования, необходимого каждому современному человеку. Исходя из этого, для студента-гуманитария математика – это, прежде всего, общеобразовательная дисциплина, как, например, право для студента-математика.
Но значение математики этим не исчерпывается. Напомним слова М.Ломоносова: «Математику уже затем учить следует, что она ум в порядок приводит». Математика влияет на упорядочение ума общностью и абстрактностью своих конструкций. Математика полна всякого рода правил, общих, строго определенных методов решения различных классов однотипных задач. Решая любую задачу, человек должен строго следовать точному предписанию (алгоритму) о том, какие действия и в каком порядке надо выполнить. Нередко изучающему математику приходится составлять подобные предписания, т. е. находить алгоритм.
Можно утверждать, что математика учит точно формулировать разного рода правила, предписания, инструкции и строго их исполнять (не последнее качество, необходимое, например, любому юристу). В юриспруденции, как и в математике, применяются одни и те же методы рассуждений, цель которых – выявить истину. Любой правовед, как и математик, должен уметь рассуждать последовательно, применять на практике индуктивный и дедуктивный методы. Занимаясь математикой, будущий правовед формирует свое профессиональное мышление.
Кроме того, применение математических методов расширяет возможности каждого специалиста. Существенную роль играют статистика, умение правильно обработать информацию, сделать достоверный вывод или прогноз на основании имеющегося статистического материала.
Мы живем в век математики. В настоящий момент одни науки уже безоговорочно приняли математику на вооружение, другие только начали ее применять. Гуманитарии, например, относятся к последним. Среди них немало еще сомневающихся в перспективности использования математических методов. Однако в настоящее время большая их часть спорит уже не о том, «нужно ли применять», а о том – «где и как лучше применять».
Математика – это феномен общемировой культуры, в ней отражена история развития человеческой мысли. Математика, с ее строгостью и точностью, формирует личность, предоставляет в ее распоряжение важнейшие ресурсы, столь необходимые для обеспечения наилучшего будущего.
Итак, математическое образование важно с различных точек зрения:
- логической — изучение математики является источником и средством активного интеллектуального развития человека, его умственных способностей;
- познавательной – с помощью математики познается окружающий мир, его пространственные и количественные отношения;
- прикладной – математика является той базой, которая обеспечивает готовность человека как к овладению смежными дисциплинами, так и многими профессиями, делает для него доступным непрерывное образование и самообразование;
- исторической – на примерах из истории развития математики прослеживается развитие не только ее самой, но и человеческом культуры в целом;
- философской – математика помогает осмыслить мир, в котором мы живем, сформировать у человека развивающиеся научные представления о реальном физическом пространстве.
Контрольные вопросы
1 Приведите 2-3 распространенных в литературе определения понятия «математика».
2 Какие определения, аксиомы и постулаты привел Евклид в своих «Началах» в III в. до н.э.?
3 В чем заключается сущность аксиоматического метода?
4 Какое место занимает математика в системе других наук?
5 В чем важность математического образования?
6 Перечислите основные математические структуры. Чем они характеризуются?
7 Для чего математика нужна гуманитарию?
8 Перечислите недостатки системы аксиом Евклида.
9 Назовите геометрии, отличающиеся от геометрии Евклида. В чем состоит их отличие?
10 Какие понятия называют основными неопределяемыми понятиями?
11 Что значит определить понятие?
12 Что такое аксиома, теорема?
Тема 2: Элементы теории множеств
Каждый с самого рождения бессознательно пользуется теорией множеств, так же как Мольеров Журден из «Мещанина во дворянстве» разговаривает прозой, сам того не ведая.
М. Стоун
Основные понятия теории множеств
В конце XIX века в математической науке возникла необходимость уточнить смысл таких ведущих понятий, как функция, непрерывность и т. д. Для этого нужно было строго определить, что такое натуральное число. Поиски ответа на эти сложные вопросы способствовали развитию новых математических идей, поэтому в конце XIX начале XX столетий происходил пересмотр старых представлений буквально во всех областях математических знаний. В результате в конце XIX века возникла новая область математики – теория множеств, одним из создателей которой был немецкий математик Георг Кантор (1845 – 1918). За небольшой срок теория множеств стала фундаментом всей математики.
Понятие множества является ключевым в математике, без которого невозможно изложение ни одного из ее разделов. Подсознательно первые представления о множестве у человека начинают формироваться с рождения, когда он погружается в многообразный мир окружающих его объектов и явлений. С первых же шагов мы не просто пополняем список знакомых нам объектов и явлений, а начинаем дифференцировать и классифицировать (горячие и холодные, сладкие и горькие, тяжелые и легкие и т. п.), объединяя тем самым объекты в некоторые совокупности.
В математике понятие «множество» используется для описания предметов или объектов. При этом предполагается, что предметы (объекты) данной совокупности можно отличить друг от друга и от предметов, не входящих в эту совокупность.
Создатель теории множеств Г. Кантор определил множество как «объединение в одно целое объектов, хорошо различимых нашей интуицией или мыслью», а также «множество есть многое мыслимое нами как единое». Эти слова не могут рассматриваться как математически строгое определение множества, такого определения не существует. Понятие множества относится к исходным (не определяемым), на основании которых строятся остальные понятия математики.
Множество – это совокупность каких-либо объектов. Так, можно говорить о множестве всех книг данной библиотеки, множестве всех вершин данного многоугольника, множестве всех натуральных чисел, множестве всех точек данной прямой и т. д. Объекты, входящие в данное множество называются элементами множества. Книги данной библиотеки, вершины данного многоугольника, натуральные числа, точки данной прямой являются элементами соответствующих множеств.
Множества обычно обозначаются большими буквами A, B, X, а их элементы – малыми буквами а, b, x.
Множество называется конечным, если количество его элементов можно выразить целым неотрицательным числом (причем неважно, известно это число или нет, главное, оно существует), в противном случае множество называется бесконечным.
Пример 1. Множество книг в библиотеке, множество студентов в группе являются конечными. Множество натуральных чисел, множество точек прямой являются бесконечными.
Количество элементов множества обозначается | A|.
Пример 2. Пусть В – множество правильных многоугольников. Тогда В = {тетраэдр, куб, октаэдр, додекаэдр, икосаэдр}. |B| = 5.
Запись x 
Х, означает что объект х есть элемент множества Х, читается «х принадлежит множеству Х», «х входит в множество Х». Если х не принадлежит множеству Х, то пишут х 
Х.
Например, если через N обозначим множество натуральных чисел, то 3 N, 20 N, 0 N, 
N.
Если все элементы множества А принадлежат какому-то множеству В, то говорят, что множество А является подмножеством множества В. Записывают А 
В (множество А содержится во множестве В). Любое множество является подмножеством самого себя, т. е. справедливо утверждение А А.
Если множество не содержит ни одного элемента, то его называют пустым и обозначают символом Ø. Пустое множество является подмножеством любого множества.
Подмножества, которые содержат не все элементы множества В, называют собственными подмножествами множества В.
Пример 3. Дано множество М = {a; c; m}. Найти все его подмножества.
Решение:
M1 = {a}, M2 = {c}, M3 = {m}, M4 = {a; c}, M5 = {a; m}, M6 = {c; m}, M7 = {a; c; m}, M8 = Ø.
Множества M7 и M8 называются несобственными подмножествами множества М.
Множества А и В называют равными (А = В), еслиони состоят из одних и тех же элементов, т.е. В А и А В.
Например, множества А = {3, 5, 7, 9} и В = {7, 3, 9, 5} равны, т. к. состоят из одинаковых элементов.
Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:
Ν ={1; 2; 3;...; n;...} – множество натуральных чисел (чисел, которые используют при счете предметов);
Ζ0 ={0; 1; 2;...; n;...} – множество целых неотрицательных чисел;
Ζ ={0; ±1; ±2;...; ± n;...} – множество целых чисел (натуральные числа и им противоположные);
Q ={ 
: m Z, n N } – множество рациональных чисел (числа, которые можно представить в виде обыкновенной дроби: целые числа, конечные десятичные и бесконечные десятичные периодические дроби);
R – множество действительных чисел (рациональные и иррациональные, т.е. бесконечные десятичные непериодические дроби).
Между этими множествами существует соотношение: 
.
Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью, или бесконечной периодической дробью. Так, ½=0,5 (=0,5000…), ⅓=0,333… – рациональные числа.
Действительные числа, не являющиеся рациональными, называются иррациональными. Иррациональное число выражается бесконечной непериодической дробью. Например,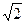 
= 1,4142356…, π = 3,1415926… – иррациональные числа.
Способы задания множеств
Понятие множества мы используем без определения. Но как узнать, является та или иная совокупность множеством или не является?
Считают, что множество определяется своими элементами, т.е. множество задано, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит.
Множество можно задать, перечислив все его элементы. Например, если мы скажем, что множество А состоит из чисел 3, 4, 5, и 6, то мы задали это множество, поскольку все его элементы окажутся перечисленными. При этом возможна запись, в которой перечисляемые элементы заключаются в фигурные скобки: А = {3, 4, 5, 6}.
Однако если множество бесконечно, то его элементы перечислить нельзя. Трудно задать таким способом и конечное множество с большим числом элементов. В таких случаях применяют другой способ задания множества: указывают характеристическое свойство его элементов.
Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
Рассмотрим, например, множество А двузначных чисел: свойство, которым обладает каждый элемент данного множества, – «быть двузначным числом». Это характеристическое свойство дает возможность решать вопрос о том, принадлежит какой-либо объект множеству А или не принадлежит. Так, число 45 содержится в множестве А, поскольку оно двузначное, а число 145 множеству А не принадлежит, так как оно не является двузначным.
Случается, что одно и то же множество можно задать, указав различные характеристические свойства его элементов. Например, множество квадратов можно задать как множество прямоугольников с равными соседними сторонами и как множество ромбов с прямым углом.
В тех случаях, когда характеристическое свойство элементов множества можно представить в символической форме, возможна соответствующая запись множества. Например, множество А натуральных чисел, меньших 7, можно задать так: А = { х | х N и х < 7}. При такой записи буквой х обозначается элемент множества А. Для этих целей можно использовать и другие буквы латинского алфавита.
Пример 4. Даны множества: М = {2; 3; 5; 7}, N = {-5; -4; -3; -2}, F = {x| x Z, -6 < x < -1}, D = {x| x N, x < 10, x – простое число}. Какие множества равны между собой?
Решение: Множества F и D заданы характеристическими свойствами. Для того, чтобы сравнить их между собой и с остальными множествами, сформулируем их характеристические свойства словами, а затем зададим их перечислением элементов.
F – множество целых чисел, больших «-6» и меньших «-1». Этому свойству удовлетворяют числа -5, -4, -3, и -2. Из этих чисел состоит множество N. Значит, F = N.
D – множество натуральных чисел, которые меньше 10 и являются простыми. Этому свойству удовлетворяют числа 2, 3, 5 и 7. Из этих чисел состоит множество M. Следовательно, D = M.
Операции над множествами
Пересечение множеств
Рассмотрим два множества: Х = {0, 1, 3, 5}, Y = {1, 2, 3, 4}.
Числа 1 и 3 и только они принадлежат одновременно обоим множествам Х и Y. Составленное из них множество {1, 3} содержит все общие для множеств Х и Y элементы.
Множество, состоящее из всех элементов, принадлежащих и множеству А, и множеству В, называется пересечением множеств А и В и обозначается А ∩ В. А ∩ В = {х А и х В}.
Таким образом, множество {1, 3} является пересечением рассмотренных множеств Х и Y: {0, 1, 3, 5} ∩ {1, 2, 3, 4} = {1, 3}.
В том случае, когда множества А и В не имеют общих элементов, говорят, что их пересечение пусто и пишут: А ∩ В = Ø.
Пересечение любого множества А с пустым множеством есть пустое множество: А ∩ Ø = Ø.
Алгебраические операции над множествами и их свойства излагаются обычно с применением кругов Эйлера или диаграмм Венна (или диаграмм Эйлера-Венна).
Пересечением множеств А и В, у которых есть общие элементы, будет заштрихованная область.
А ∩ В
Если множества не имеют общих элементов, то их пересечение будет выглядеть так:
Если одно из множеств является подмножеством другого, то их пересечение будет выглядеть так:
Объединение множеств
Вновь возьмём множества Х = {0, 1, 3, 5} и Y = {1, 2, 3, 4} и наряду с ними рассмотрим множество {0, 1, 2, 3, 4, 5}. Это множество содержит все элементы множества Х и все элементы множества Y и не содержит никаких других элементов.
Множество, состоящее из всех элементов, принадлежащих или множеству А или множеству В, называется объединением множеств А и В, обозначается А U В. А U В = { х А или х В }
Итак, {0, 1, 3, 5} 
{1, 2, 3, 4} = {0, 1, 2, 3, 4, 5}.
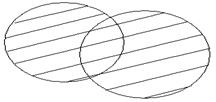Если изобразить множества А и В при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью.
А U В
Если множества не имеют общих элементов, то их объединение выглядит так:
А U В
Если одно из множеств является подмножеством другого, то их объединение будет выглядеть так:
 |
А U В
Часто приходится рассматривать объединение и пересечение трёх и более множеств. Объединение множеств А, В и С есть множество, каждый элемент которого принадлежит хотя бы одному из множеств А, В или С; пересечение множеств А, В и С есть множество всех элементов, принадлежащих и множеству А, и множеству В, и множеству С.
А U В U С 
А ∩ В ∩ С
Например, объединение множеств остроугольных, тупоугольных и прямоугольных треугольников есть множество всех треугольников.
Еще операции над множествами можно показать с помощью детского анекдота: Однажды лев, царь зверей, собрал зверей на поляне и повелел им разделиться на умных и красивых. После того, как пыль улеглась, лев увидел на поляне две большие группы зверей и мартышку, прыгающую между ними. На вопрос: почему она прыгает туда-сюда, мартышка ответила: «Что мне, разорваться, что ли?». Так вот, мартышка из анекдота – это пример пересечения умных зверей и красивых. А объединением умных и красивых зверей является все множество зверей.
Объединение и пересечение множеств обладают многими свойствами, аналогичными свойствам суммы и произведения чисел:
| № п/п | Свойство операций над множествами | Свойство арифметических операций | Название свойства |
| a + b = b + a | Коммутативность | |
| 
| ||
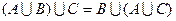
| (а+b)+c = a+(b+c) | Ассоциативность | |
| 
| ||
| 
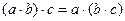
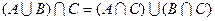
| Дистрибутивность |
Однако эта аналогия не всегда имеет место. Например, для множеств справедливы равенства:
6 (А U С) ∩ (В U С) = (A ∩ B) U С.
7 А U А = А.
8 А ∩ А = А.
Соответствующие равенства для чисел верны не всегда.
Заметим, что, если в выражении есть знаки пересечения и объединения множеств, и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение.
Вычитание множеств
Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания называют разностью и определяют следующим образом.
Разностью множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и не принадлежат множеству В, обозначается А \ В. А \ В = { х А и х В }.
Х \ Y = {0, 1, 3, 5} \ {1, 2, 3, 4} = {0, 5}. Если мы найдем разность множеств Y и Х, то результат будет выглядеть так: Y \ X = {2; 4}. Таким образом, разность множеств не обладает переместительным (коммутативным) свойством.
Если изобразить множества А и В при помощи кругов Эйлера, то разность данных множеств изобразится заштрихованной областью.
А \ В
Если множества не имеют общих элементов, то их разность будет изображаться так:
 |
 |
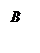А \ В
Если одно из множеств является подмножеством другого, то их разность будет изображаться так:
А \ В
Пересечение – более «сильная» операция, чем вычитание. Поэтому порядок выполнения действий в выражении А \ В ∩ С такой: сначала находят пересечение множеств В и С, а затем полученное множество вычитают из множества А. Что касается объединения и вычитания множеств, то их считают равноправными. Например, в выражении А \ В U С надо сначала выполнить вычитание (из А вычесть В), а затем полученное множество объединить с множеством С.
Вычитание множеств обладает рядом свойств:
1 (А \ В) \ С = (А \ С) \ В.
2 (А U В) \ С = (А \ С) U (В \ С).
3 (А \ В) ∩ С = (А ∩ С) \ (В ∩С).
4 А \ (В U С) = (А \ В) ∩ (А \ С).
5 А \ (В ∩ С) = (А \ В) U (А \ С).
Дополнение
В случаях, когда одно из множеств является подмножеством другого, А \ В называют дополнением множества В до множества А, и обозначают символом В'А
Пусть В А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В. В А, А \ В = В ' А, В ' А = { х | х А и х В }.
Часто ограничиваются рассмотрением всевозможных подмножеств одного и того же множества, которое в этом случае называют основным или универсальным множеством. Обозначим основное множество буквой E. Для любого множества А, принадлежащего основному множеству Е, справедливы равенства: А U Е = Е, А ∩ Е = А.
Множество элементов основного множества Е, не принадлежащих множеству А, называется дополнением множества А до множества Е или просто дополнением и обозначается А'.
Объединение множества А и его дополнения А' есть основное множество: А U А' = E.
Пересечение множества со своим дополнением пусто: А ∩ А ' = Ø.
Дополнение пустого множества есть основное множество: Ø' = E, а дополнение основного множества пусто: Е' = Ø.
На рисунке основное множество Е схематически изображено в виде прямоугольника, его подмножество А заштриховано, не заштриховано дополнение множества А'.
Формула Грассмана
Теория множеств используется при решении задач следующего вида:
В группе зверей 15 умных, 13 – красивых, и 8 мартышек. Сколько зверей в группе?
Решение:
Пусть U – множество умных зверей, К – множество красивых. Тогда множество мартышек будет обозначаться как 
, а множество всех зверей – 
. Значит, | U| = 15, |K| = 13 и 
= 8. Требуется найти 
. Так как мартышки входят как в множество умных, так и в множество красивых, то при простом сложении элементов множеств, мы мартышек посчитаем два раза. Тогда из суммы элементов множеств умных и красивых нужно одну часть мартышек вычесть. Получим формулу: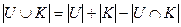 
. Эта формула носит название формулы Грассмана для двух множеств. С помощью этой формулы найдем количество зверей: = 15 + 13 – 8 = 20.
Пример 5. В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
Решение:
Изобразим ситуацию, изложенную в задаче, с помощью кругов Эйлера:
Тогда |E| = 35, |A| = 20, |B| = 11, |E\(A È B)| = 10. Требуется найти, чему равно | A Ç B|. Сначала найдем, чему равно | A È B|. | A È B| = |E| – |E\(A È B)| = 35 – 10 = 25. Теперь подставим известные значения в формулу Грассмана:
25 = 20 + 11 - |A Ç B|. Выразим из этого уравнения | A Ç B| и найдем, чему оно равно: | A Ç B| = 20 + 11 – 25 = 31 – 25 = 6. Таким образом, 6 учеников увлекаются и биологией, и математикой.
Контрольные вопросы
1 Назовите основателя теории множеств.
2 Дайте определение множества, элемента множества.
3 Какие способы задания множеств вы знаете?
4 Какие множества называют равными?
5 Дайте определение подмножества. Чем отличаются собственные подмножества от несобственных?
6 Какие множества называются числовыми? Приведите примеры числовых множеств.
7 Пересечение, и объединение множеств. Примеры.
8 Вычитание и дополнение множеств. Примеры.
9 Какая из операций сильнее (выполняется раньше)?
10 Как изображаются операции над множествами с помощью диаграмм Эйлера-Венна?
11 Перечислите свойства операций над множествами.
12 Для решения каких задач используют формулу Грассмана?
Тема3: Элементы математической логики
…Встреча математики с логикой в прошлом столетии привела к таким же последствиям, что и приход принца в зачарованный замок спящей красавицы: после столетий глубокого сна логика вновь расцвела плодотворной жизнью.
Л.Э. Гуревич, Э.Б. Глинер
Введение
Слово «логика» всем хорошо знакомо. Его часто можно встретить на страницах всевозможных печатных изданий, услышать в разговорной речи. Что же означает это слово? Заглянем в толковый словарь С.И. Ожегова. Там сказано: «Логика – наука о законах мышления и его формах» и еще – «Логика – ход рассуждений». Если второе толкование смысла слова «логика» более или менее понятно каждому, то в связи с первым сразу возникает вопрос: а что такое формы и законы мышления?
Подобно Журдену из пьесы Мольера «Мещанин во дворянстве», который очень обрадовался, узнав, что всю жизнь говорит прозой, вам будет приятно узнать, что в большинстве случаев вы мыслите и говорите по законам логики.
Слово «логика» происходит от греческого logos, что, с одной стороны, означает «слово», а с другой – «мысль, рассуждение». Логика изучает акты мышления, зафиксированные в языке в виде слов, предложений и их совокупностей. Таким образом, логика имеет непосредственное отношение к языку, речи, т.е. соприкасается с грамматикой и, более широко, с лингвистикой (наукой о языке). С помощью логических средств наш естественный язык уточняется, приобретает четкость и определенность. Как справедливо заметил польский логик А.Тарский, – логика создает возможность лучшего взаимопонимания между теми, кто к этому стремится.
Многим хорошо известно, что логика – неотъемлемая составная часть математики. Без логики в математике – ни шагу: ни тебе теорему доказать, ни формулу вывести, ни задачу решить. Ироническая фраза: «Нематематики считают, что математики считают» намекает на то, что основное занятие математиков – вовсе не счет (как многие полагают), а логические или, иначе говоря, дедуктивные рассуждения – выводы, доказательства. (Слово дедукция происходит от латинского deduction, что значит – выведение). С помощью логики математики выводят из уже имеющихся в их распоряжении математических фактов новые факты.
В этом и заключаются основное назначение и сила логики: с ее помощью, имея некоторый запас достоверных (истинных) знаний, можно получать новые знания, не прибегая к наблюдению или эксперименту, а лишь размышляя и рассуждая по определенным правилам.
Логика входит в арсенал методов любой науки, является частью ее методологии. Многие естественнонаучные факты были открыты с помощью логики.
Однако в математике логика выступает в наиболее отчетливом, нестертом, незавуалированном виде, а ее «удельный вес» несравненно больше, чем в естественных науках. В математической теории количество предложений, содержащих исходное знание (аксиом), сводится к минимуму; основное же содержание теории заключено в предложениях, полученных в результате логических рассуждений (теоремах). Поэтому математику называют дедуктивной наукой в отличие от естественных наук (физики, химии, биологии), в которых основной, ведущий метод – эксперимент. Впрочем, естественные и даже многие гуманитарные науки по мере своего развития все более активно и плодотворно используют математические и логические методы, а возможность представления содержания какой-либо науки (или ее раздела) в виде аксиоматической теории считается показателем высокой степени развития этой науки. Как полагал великий немецкий философ Эммануил Кант (1724-1804 гг.), – «каждая наука в той или иной мере является наукой, в какой мере содержит математику». Быть может, это сказано слишком сильно, однако, этой фразой емко и выразительно определено значение математики для других наук и ее место среди них. Недаром другой знаменитый ученый, наш соотечественник, физик Лев Ландау (1908-1968 гг.) назвал математику «наукой сверхъестественной».
Итак, логика в большей или меньшей степени используется как один из методов в любой науке. Необходима логика и в повседневной жизни. С ее помощью обеспечивается полноценное (адекватное) общение в мире людей и компьютеров. Логика присутствует или, по крайней мере, должна присутствовать в любом споре, судебном разбирательстве, расследовании преступления (Шерлок Холмс и его дедуктивный метод!).
В высшей степени важна логика в законотворчестве: формулировка закона должна исключать возможность его неоднозначного толкования. «Логика – это необходимый инструмент, освобождающий от лишних, ненужных запоминаний, помогающий найти в массе информации то ценное, что нужно человеку. Без логики – это слепая работа» – так сказал о роли логики в познавательной, в частности в учебной деятельности, академик П. Анохин.
Почему же логика – столь универсальный инструмент, полезный, более того – необходимый в любой интеллектуальной деятельности? Чем объясняется ее общезначимость? Рассмотрим три рассуждения.
1 Все насекомые – шестиногие. У паука – не шесть ног (а восемь!). Следовательно, паук не насекомое.
2 Все числа, кратные 10, оканчиваются нулем. Число п не оканчивается нулем. Следовательно, число п не кратно 10.
3 Все отличники в Петином классе занимаются спортом. Петя не занимается спортом. Следовательно, Петя – не отличник.
Все эти короткие, одношаговые рассуждения (умозаключения) имеют одну и ту же форму: Все А – это В; не В. Следовательно, не А. Умозаключение такой формы всегда приводит к верному (истинному) выводу (заключению, следствию), если исходные утверждения (посылки) истинны. Формы рассуждений, обладающие свойством «перерабатывать» любые истины в новые истины, называются правильными. Логика дает нам свод правильных форм основных, простейших рассуждений (умозаключений) и правила построения из них сколь угодно длинных и сложных дедуктивных рассуждений, которые применимы в любой области знаний. Этим и объясняется универсальность и «вездесущность» логики, ни с чем не сравнимое многообразие сфер ее применения.
Логика, хотя и связана с языком, но, в отличие от лингвистики, изучает не формы языка, а отраженные в языке формы мышления. А, как известно, несмотря на все различия языков, человечество имеет общее достояние в виде некоторой совокупности мыслей. Идея универсальности логики была использована при создании линкоса, языка для связи с инопланетными цивилизациями. При этом предполагалось, что логические формы и законы, свойственные человеческому мышлению, присущи всякому разуму, и что поэтому такой «логический» язык вместе с языком математических абстракций может стать средством общения в самом широком смысле и масштабе.
Логика как наука сформировалась очень давно – в IV в. до н.э. Ее создал древнегреческий ученый Аристотель. В течение многих веков логика сколько-нибудь существенно не развивалась. Это, конечно, свидетельствует о гениальности Аристотеля, которому удалось создать столь полную научную систему, что, казалось, «не убавить, не прибавить». Однако в силу такой неизменности логика приобрела славу мертвой, застывшей науки и вызывала у многих скептическое к себе отношение. Сухость и кажущуюся закостенелость, бесплодность логики высмеяли в своих бессмертных произведениях Ф. Рабле и Д. Свифт («Гаргантюа и Пантагрюэль» и «Путешествие Гулливера»). В XVII в. великий немецкий ученый Готфрид Лейбниц (1646-1716) задумал создать новую логику, которая была бы «искусством исчисления». В этой логике, по мысли Лейбница, каждому понятию соответствовал бы символ, а рассуждения имели бы вид вычислений. Эта идея Лейбница, не встретив понимания современников, не получила в то время распространения и развития.
Только в середине XIX в. ирландский математик и логик Джордж Буль (1815-1864) частично воплотил в жизнь идею Лейбница. Им была создана алгебра логики, в которой действуют законы, схожие с законами обычной алгебры, но буквами обозначаются не числа, а предложения. На языке булевой алгебры можно описывать рассуждения и «вычислять» их результаты; однако, ею охватываются далеко не всякие рассуждения, а лишь определенный тип их, в некотором смысле – простейший.
Алгебра логики Буля явилась зародышем новой науки – математической логики. В отличие от нее логику, восходящую к Аристотелю, называют традиционной или классической формальной логикой. Таким образом, математическая логика – это логика, использующая язык и методы математики.
Математическая логика сама стала областью математики, поначалу казавшейся в высшей степени абстрактной и бесконечно далекой от практических приложений. Сегодня математическая логика используется в биологии, медицине, лингвистике, педагогике, психологии, экономике, технике. Велика роль математической логики в развитии вычислительной техники: она используется в конструировании компьютеров и при разработке искусственных языков для общения с ними.
