Зельнер і Гейл [1] запропонували трикроковий метод найменших квадратів, який за певних обставин є більш ефективним, ніж двокроковий.
Розглянемо загальну лінійну модель, яка містить r взаємозв’язаних ендогенних і k екзогенних змінних. Запишемо s -те рівняння цієї моделі у вигляді
(11.45)
де 
— вектор значень ендогенної змінної s -го рівняння розміром n 1;
— матриця поточних ендогенних змінних s -го рівняння, розміром n r;
— матриця екзогенних змінних s -го рівняння, розміром n 
;
і 
— вектори параметрів;
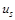— вектор залишків.
Об’єднавши дві матриці і в матрицю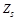 
, перепишемо (11.45) у вигляді:
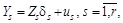(11.46)
де 
і 
. (11.47)
Помножимо рівняння (11.46) зліва на 
, де X — матриця всіх екзогенних змінних моделі, розміром n k:
(11.48)
Для цієї моделі коваріаційна матриця залишків має вигляд
(11.49)
де 
— стала дисперсія залишків s -го рівняння, а 
— дисперсія залишків системи рівнянь моделі. З урахуванням (11.49) оцінка параметрів моделі (11.48) може бути виконана узагальненим методом найменших квадратів.
. (11.50)
Запишемо систему рівнянь (11.46) у вигляді такої матричної форми:
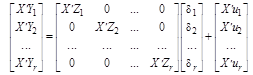. (11.51)
Матриця коваріацій для вектора залишків, який входить в рівняння (11.51) буде мати вигляд:
. (11.52)
Нехай елементи матриці 
створюють матрицю S, тод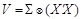і 
і 
. Метод Ейткена дає наближені оцінки параметрів системи (11.51). Але для того щоб одержати ці оцінки, необхідно знати матрицю V, яка залежить від невідомої матриці S.
Зельнер і Гейл [1] запропонували обчислювати елементи матриці S на основі залишків, здобутих за допомогою двокрокового методу найменших квадратів. Тобто, двокроковий метод застосовується при оцінюванні параметрів 
за формулою (11.50) для кожного структурного рівняння. Після чого знайдені оцінки підставляються в (11.46). Обчислюються значення 
, з допомогою яких можна знайти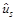 
.
На основі 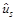визначаються дисперсії залишків для кожного рівняння 
, які є наближеною оцінкою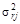 
.
Звідси оператор оцінювання на основі трикрокового методу найменших квадратів матиме вигляд:
(11.53)
Оцінку асимптотичної матриці коваріацій параметрів дає обернена матриця, яка міститься в правій частині виразу (11.53), тобто
(11.54)
Трикроковий метод найменших квадратів забезпечує кращу порівняно з двокроковим методом асимптотичну ефективність оцінок лише в тому разі, коли матриця 
не є діагональною, тобто коли залишки, які входять в різні рівняння моделі, корелюють між собою.
Щоб застосувати трикроковий метод найменших кввадратів на практиці необхідне виконання таких вимог:
1) усі тотожності, які входять в систему рівнянь, треба виключити, приступаючи до знаходження оцінок параметрів;
2) кожне неідентифіковане рівняння також треба виключити з системи;
3) якщо система рівнянь, що залишилась, має точно ідентифіковані і надідентифіковані рівняння, то трикроковий метод оцінки доцільно застосовувати до кожної з цих груп;
4) для групи надідентифікованих рівнянь оцінки параметрів знаходяться на основі співвідношення (11.53), взявши значення r таким, що дорівнює числу надідентифікованих рівнянь;
5) якщо група надідентифікованих рівнянь має тільки одне рівняння, то трикроковий метод перетворюється на двокроковий;
6) якщо матриця коваріацій для структурних залишків блочно-діагональна, то вся процедура оцінювання на основі трикрокового методу найменших квадратів може бути застосована окремо до кожної групи рівнянь, які відповідають одному блоку.
