Помилки специфікації моделі можуть бути трьох видів:
1) ігнорування істотної пояснюючої змінної при побудові економетричної моделі;
2) введення до моделі незалежної змінної, яка не стосується вимірюваного зв’язку;
3) використання не відповідних математичних форм залежності.
1) Для відшукання цього джерела помилок специфікаціі досить важко запропонувати які-небудь загальні міркування, оскільки незалежна змінна, що не враховується (або незалежні змінні), може бути одним із багатьох можливих пояснень. Про необхідність введення моделі до цих незалежних змінних можна лише здогадуватись на підставі апріорних міркувань. Проте відомі й більш формалізовані процедури, які дають змогу з’ясувати, наскільки істотним є введення до моделі якої-небудь змінної. Так, наприклад, якщо побудувати економетричну модель на базі покрокової регресії (метод покрокової регресії розглянемо пізніше), то можна досить чітко ранжувати пояснювальні змінні за величиною їх впливу на залежну змінну. Про відсутність основної змінної свідчить зміна поводження випадкового відхилення у помилково специфікованій моделі.
Див питання 63
64. Оператор оцінювання Вальда.
Нехай економетрична модель має вигляд
(9.14)
У такому разі, якщо вибіркова сукупність містить парне число спостережень, то матриця інструментальних змінних Z запишеться так:
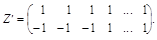
Щоб визначити другий рядок цієї матриці, необхідно виконати такі дії
1. знайти відхилення кожного елемента вектора X від медіани.
Матриця пояснювальних змінних для цієї моделі запишеться у вигляді:
Матриця інструментальних змінних на основі даної матриці замість рядка пояснювальної змінної міститиме рядок інструментальної.
2. величини відхилень, що мають знак «плюс», замінюються на одиниці, величини відхилень, що мають знак «мінус», — на одиниці з цим знаком.
Використовуючи оператор оцінювання
,
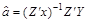маємо:
(9.15)
де 
і 
характеризують середні відхилення значень X відповідно вгору і вниз від медіани, а 
і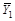 
— середні значення залежної змінної, які відповідають середнім 
і . Звідси
(9.16)
Це означає, що параметр 
у моделі (9.14) подається у вигляді:
(9.17)
причому
Коли вибіркова сукупність містить непарне число спостережень, то перш ніж розпочинати обчислення, необхідно відкинути середнє спостереження.
При загальних припущеннях оцінка, яка здобута методом Вальда, є обгрунтованою, але її вибіркова дисперсія може бути досить великою, тобто оцінка є неефективною.
