Приклади економетричних моделей: моделі пропозиції і попиту на конкурентному ринку
На конкурентному ринку рівновага обміну встановлюється через рівновагу між пропозицією і попитом. Нехай g1 і g2 — кількість попиту і пропозиції деякого продукту в певний день на деякому ринку; p — ціна, за якою реалізується продукція. Величини g1 і g2 залежать від p, оскільки ціна не влаштовує покупців і продавців, то кількість проданого товару зменшується. У результаті можна записати дві функції:
g1 = f(p, u) — функцію попиту;
g2 = Y(p, e) — функцію пропозиції.
Знаючи ціну p, можна визначити величини попиту і пропозиції. Для існування рівноваги на ринку необхідно, щоб виконувалась рівність. Отже, модель має такий вигляд:
g1 = g2;
g1 = f(p, u); (2.6)
g2 = Y(p, e).
До неї входять дві функції, що характеризують залежність попиту і пропозиції від ціни, а також тотожність.
В реальних умовах попит і пропозиція певного товару залежать не лише від його ціни, а й від цін товарів, які можуть заміняти або доповнювати розглядуваний товар. Попит і пропозиція залежать також від інших чинників, наприклад, попит залежить від доходу покупців, а пропозиція від виробничих умов і т.ін. Тоді модель (2.6) можна записати так:
g1t = f(pt, X1t, X2t,... Xmt, ut);
g2t = Y(pt – 1, X1t, X2t,... Xmt, et); (2.7)
g1t = g2t.
В цій моделі на відміну від попередньої попит у періоді t залежить від ціни в цьому самому періоді, а пропозиція в періоді t залежить від ціни попереднього періоду (t – 1).
Нехай залежність попиту і пропозиції від факторів, що впливають на них, лінійна. Тоді економетрична модель запишеться так:
g1t = a0 + a1pt + a2X1t + a3X2t +... + am Xmt + ut;
g2t = b0 + b1pt – 1 + b2X1t + b3X2t +... + bm Xmt + et; (2.8)
g1t = g2t.
Приклади економетричних моделей: модель Кейнса
Розв’язання проблеми безробіття було головною турботою Кейнса. Він намагався пояснити рівень виробництва в період неповного завантаження робочої сили та обладнання. Ці намагання привели до висновків, що капіталовкладення відіграють основну роль в кон’юнктурній еволюції з двох причин:
1) рішення про інвестиції значною мірою є автономними, вони впливають на зростання обсягів виробництва у двох секторах — предметів споживання та засобів виробництва;
2) зростання обсягів виробництва збільшує доходи, а останні, у свою чергу, впливають на збільшення обсягу виробництва предметів споживання.
Покажемо, як наведені щойно міркування можна спрощено подати у вигляді моделі.
Нехай P — загальний обсяг продукції; C — виробництво предметів споживання; I — виробництво засобів виробництва (що дорівнює капіталовкладенням); R — доходи, які розподіляються. тоді модель запишеться так: P = C + I; C = F (R, u); R = P.
У цій моделі I задається автономно, а F є функція, що визначає відповідність між споживанням і розподіленими доходами.
З трьох записаних щойно рівнянь можна дістати таке рівняння: P – F (R,u) = I.
Розв’язавши його відносно P, знайдемо рівень виробництва, який пов’язаний з рівнем капіталовкладень. Так, наприклад, якщо F (R) є лінійна функція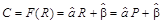 
, то рівняння (2.9) набирає вигляду 
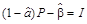, звідки 
Рівняння (2.11) визначає залежність обсягу виробництва P від обсягу капіталовкладень I, які задаються автономно. Коефіцієнти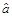 
і 
в цьому рівнянні залежать від функції споживання (2.10), тобто від зв’язку між R і C. Зокрема, ця функція вимірює збільшення споживання 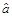, яке пов’язане зі збільшенням доходу на одиницю і називається «граничною схильністю до споживання». Значення 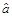, як правило, менше за одиницю. Зокрема, у моделі Кейнса 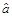= 0,6. Залежність (2.11) показує при цьому, що збільшення капіталовкладень на одиницю зумовлює зростання обсягу виробництва на 1 / (1 – 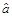)— коефіцієнт, який завжди перевищує одиницю (при 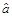= 0,6 маємо 1 / 1 – 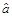= 2,5). Цей коефіцієнт вимірює ефект взаємозв’язку між автономним зростанням капіталовкладень та обсягом виробництва і називається мультиплікатором.
