Раніше ми припускали, що змінні вимірюються без помилок, і лише відхилення u — це єдина припустима форма помилок. Останнє було пов’язане з наміром врахувати вплив різних пояснювальних змінних, які не входять до економетричної моделі в явному вигляді.
Проте досить часто при вимірюванні змінних, які належать до економетричної моделі, припускаються помилок. Тоді постає запитання, як наявність помилок змінних може вплинути на оцінку параметрів моделі?
Щоб відповісти на це запитання, розглянемо матрицю незалежних змінних X, елементи якої містять помилки.
Нехай
(9.22)
де 
— матриця розміром n m справжніх (фактичних) значень, а V — матриця помилок вимірювання.
Тоді модель має вигляд
або
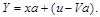(9.23)
Оцінка параметрів для цієї моделі 1МНК матиме вигляд
,
де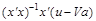 
— величина зміщення оцінки.
Обгрунтованість цієї оцінки залежить від того, чи дорівнює нулю
.
Запишемо
За припущення, що залишки u не корелюють гранично зі змінними X (як зі справжніми значеннями, так і з їх помилками), можна стверджувати таке:
.
Проте
Отже, навіть тоді, коли помилки вимірювання змінних X не корелюють зі справжніми значеннями цих змінних і перший доданок у правій частині дорівнює нулю, другий доданок, який характеризує матрицю коваріацій помилок, здебільшого не дорівнює нулю. А це означає, що за наявності помилок вимірювання змінних оцінка параметрів моделей 1МНК є необгрунтованою і асимпотичне зміщення визначається формулою
Наприклад, якщо ми оцінюємо параметри моделі з двома змінними 1МНК, то зміщення
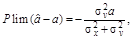
або
(9.24)
де 
— дисперсія помилки вимірювання X, а 
— дисперсія справжніх значень X, причому припускаємо, що помилки вимірювання не корелюють із цими значеннями X.
Рівняння (9.24) показує, що оцінка справжнього значення параметра моделі занижена. Наприклад, як би ми не збільшували сукупність спостережень, якщо = 10 % від , то оцінка параметра 
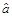відрізнятиметься від справжнього значення також майже на 10 %, тобто за наявності помилок вимірювання змінних збільшення сукупності спостережень не компенсує зміщення.
Тому при оцінюванні параметрів економетричної моделі, коли трапляються помилки вимірювання змінних, доцільно застосувати метод інструментальних змінних, який ми розглянули раніше.
Алгоритм Уоліса
Уоліс запропонував складніший трикроковий метод оцінювання.
Крок 1. Оцінюються параметри моделі
,
де 
використовується як інструментальна змінна для 
. Таким чином, визначають:
де
і 
, 
.
Крок 2. Для залишків цієї моделі 
розраховують коефіцієнт автокореляції першого порядку з урахуванням поправки на зміщення:
де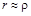 
.
Крок 3. За допомогою оцінки, здобутої для r, формують матрицю:
і обчислюють оцінку вектора 
узагальненим методом найменших квадратів:
Проведені Уолісом експерименти показали, що його метод оцінювання приводить до значно менших величин зміщення і до меншої суми квадратів залишків, ніж застосування методу Ейткена.
