Незважаючи на численність робіт, присвячених проблемам забезпечення фінансової стійкості страхових операцій, на сьогоднішній день немає прийнятної математичної моделі, яка б відтворювала механізм страхової діяльності і дозволяла здійснювати оцінку альтернативних стратегій розвитку страхових операцій та кількісних параметрів управлінських рішень, її створення суттєво ускладнюється тим, що надходження страхових платежів, настання страхових випадків і пов'язані з ними зміни капіталу компанії є випадковими процесами, і тому в якості моделі страхової компанії необхідно розглядати сукупність стохастичних фінансових потоків.
Багато існуючих моделей теорії ризику були побудовані у процесі дослідження платоспроможності страхових компаній, їхнє основне завдання - визначення мінімального розміру власних, вільних від зобов'язань, коштів страхової компанії як основної умови її динамічної платоспроможності. Однак для одержання оцінок параметрів, необхідних для прийняття менеджерами страхової компанії оптимальних управлінських та інвестиційних рішень, для розробки стратегії, спрямованої на досягнення поставленої власниками (засновниками, акціонерами) мети необхідна модель, вихідними даними якої повинні бути не тільки ймовірність виконання зобов'язань перед страхувальниками, але й імовірнісні характеристики прибутковості з відповідною множиною значень параметрів управління. Такий підхід може бути реалізований шляхом представлення страхової компанії у вигляді сукупності стохастичних фінансових потоків, що описують як найважливіші операції страховика, так і вплив основних факторів зовнішнього середовища. Ускладнення моделі порівняно з класичною постановкою необхідне для того, щоб врахувати особливості та специфічні ризики страхового ринку, що розвивається, а також економіки перехідного періоду. З метою якнайповнішого врахування впливу неконтрольованих випадкових факторів У процесі прийняття рішень щодо управління страховою компанією для побудови моделі та оптимізації її параметрів застосуємо метод імітаційного моделювання.
В умовах відсутності сформованих страхових портфелів за видами страхування, замкнутого солідарного розподілу збитку в межах виду і достатнього обсягу достовірних статистичних даних про особливості виплат за окремими договорами страхування, для моделювання страхового процесу доцільно застосовувати динамічну модель колективного ризику, яка орієнтована на визначення можливості компанії виплатити страхове відшкодування за будь-яким договором страхового портфеля у будь-який момент часу. Процеси надходження і виплат імітуються незалежно один від одного для всієї сукупності договорів страхування з якомога точнішим відтворенням особливостей цих процесів для конкретного страховика.
Тому неможливо скористатися готовою математичною моделлю. Інша складність прогнозування розвитку страхування - неможливість використати довгі часові ряди. Це стало неможливим або таким, якого важко досягти, у зв'язку з великими геополітичними змінами в країні, що відбулися за останні 10 років - розпадом Союзу, великим рівнем інфляції тощо. Звичайно, можна спробувати скласти зведений ряд, але при цьому неминучим є зниження точності прогнозування внаслідок внесення похибок. Тому прогнозування доводиться здійснювати на короткому часовому ряді. Проте не всі моделі дають змогу добитися достатньо високої точності на коротких часових рядах. Особливо актуальним це питання стає при довгостроковому прогнозуванні. Певні складності виникають також за наявності у коротких часових рядах значної випадкової складової. Це призводить до того, що задача синтезу моделей довгострокового прогнозування стає/некоректною.
Для довгострокового прогнозування використовують тренди, довгострокові тенденції, оскільки випадкова складова становить короткочасні тенденції, недоступні при довгостроковому прогнозуванні. Відомі методи виділення тренду за часовими рядами використовують поліноми лінійних форм, дробно-раціональні функції, нелінійні форми, рівняння всіляких поєднань Колмогорова-Габора та ін. Вибір апроксимуючого рівняння має дві задачі: визначення міри наближення апроксимуючої функції до емпіричних даних (часового ряду) та виду рівняння. Перша задача вирішується з використанням методу найменших квадратів, друга - становить значну складність і вирішується на основі дослідження фізичної сутності процесів при порівняно суб'єктивному виборі виду рівняння.
Слід зазначити, що динамічний ряд для сум зібраних страхових премій в Україні має квазістаціонарний характер, у всякому випадку, про квазістаціонарний характер слід зробити припущення. Тоді імовірнісні та динамічні властивості ряду залишаються незмінними в межах заданого ряду, а значення постійної складової може змінюватися. Якщо до динамічного ряду з помітною нестаціонарністю застосувати засоби перевірки на автокореляцію, то буде виявлено значний коефіцієнт автокореляції (так звана "хибна автокореляція").
Для усунення "хибної автокореляції” здійснимо виділення тренду.
Для реалізації концептуальної моделі функціонування страхової компанії необхідна методика стохастичного моделювання процесів надходження премій та виплати відшкодувань. Метою статті є підбір математичного інструментарію для адекватного відтворення процесу надходження страхових премій у процесі операційної діяльності страховика.
Процеси надходження премій та страхових виплат протікають в різних масштабах часу і мають різні масштаби вимірювання. Премії поступають значно частіше, ніж пред'являються позови, і при цьому величина премії набагато менша порівняно з сумою відшкодування. Тому в класичних моделях теорії ризику прийнято вважати процес надходження премій неперервним і детермінованим, зі сталою швидкістю надходження платежів - с. Швидкість с -єдиний параметр, за допомогою якого в моделях ризику описується даний процес: за період (0; t) в компанію надходить ct внесків. Згідно такого формулювання, процес Xt надходження внесків є стаціонарним, тобто математичне сподівання випадкової величини Xt є сталою (EXt = а) для будь-якого t, а кореляційна функція E(Xt - a) (Xs - а) залежить лише від t — s.
Такі припущення класичної моделі можна з високим ступенем впевненості застосовувати для моделювання діяльності страховиків, які працюють на розвиненому страховому ринку. Орієнтуючись на сталий сформований попит на страхові послуги (адже в країнах із ринковою економікою страхується в середньому 90-95% усіх ризиків), високу страхову культуру населення, компанії спроможні досягти такого стану страхового портфеля, за якого приплив нових договорів принаймні компенсує ті, що закінчуються, причому компенсація розповсюджується не лише на кількість договорів і суму внесків, але й на страхову суму, термін страхування, величину ризику. Для таких компаній процес надходження коштів буде неперервним зі сталою швидкістю.
Натомість абсолютна більшість страхових компаній України працюють з нестаціонарними сукупностями за відсутності рівноваги між притоком та відтоком договорів і, що найважливіше, без чітко сформованих сукупностей за видами страхування. Таким чином, розмивається поняття «вид страхування», в той час як методика розрахунку тарифів передбачає, що тарифні ставки обчислюються для замкнутої страхової сукупності.
За таких умов важко говорити про однорідність страхового портфеля, а набір різнорідних ризиків у портфелі призводить до непередбачуваності фінансових результатів, оскільки за умов неоднорідної вибірки страховик не може спиратися на статистичні закономірності.
Досягти однорідності вибірки можна лише шляхом відповідного підбору ризиків як на стадії розробки правил і умов страхування, так і на стадії фактичного формування страхового портфеля. Дослідження страхового ринку свідчать, що саме на другій стадії страховики практично не займаються відбором ризиків, працюючи за принципом «Страхуємо все!», без чіткої стратегії формування портфеля.
На підставі аналізу статистичних даних, які характеризують внески страховиків України, виявлено, що інтенсивність їхнього надходження не є сталою, а процес надходження не можна вважати стаціонарним. Навіть у великих компаній процес надходження важко охарактеризувати сталою швидкістю, оскільки дисперсія швидкості в десятки разів перевищує її математичне прогнозування. Тому при усередненні значення інтенсивності (як цього вимагає класична теорія ризику) і зведенні процесу до стаціонарного втрачається відповідність моделі реальній системі, коректність висновків, які робляться на основі дослідження моделі, точність параметрів управління системою, одержаних в результаті моделювання.
Отже, для побудови динамічної моделі страхової компанії процес надходження коштів доцільно описувати послідовністю ТІ, Т2І.. Тп, моментів їх сплати, які, як і моменти виплати відшкодувань, є випадковими, а також послідовністю незалежних випадкових величин {fk, k > 1}, що задають розмір внесків. Згідно основного твердження теорії ризику, процес настання випадкових подій і величина пов'язаних із ними надходжень (виплат) повинні розглядатися окремо, оскільки є взаємонезалежними.
Розглянемо випадковий процес

де St — сумарний обсяг внесків, здійснених протягом часу (0; t); nt — кількість внесків, які надійшли за час (0; t); Yk — величина k-ro внеску. Зробимо природні припущення про характер поведінки процесу:
1) події, пов'язані з надходженням внесків на інтервалах часу, які не перетинаються, є незалежними випадковими подіями;
2) розподіл кількості клієнтів, які уклали договори страхування в інтервалі часу [t, t + h] не залежить від t, а залежить лише від h;
3) ймовірність того, що на інтервалі [t, t + h] буде здійснено принаймні один внесок, дорівнює ah + o(h), де a – константа.
4) ймовірність надходження двох або більше внесків за проміжок часу [t, t + h] становить o(h).
За таких умов випадковий процес (1) з необхідністю є узагальненим процесом Пуассона і для будь-якого t випадкова величина nt має розподіл Пуассона з параметром М, де А, відображає середню кількість внесків за одиницю часу, тобто

Припущення про пуассонівські властивості процесу надходжень накладає певні обмеження на модель. Наприклад, однорідність nt означає незмінність портфеля компанії. Крім того, якщо Ut - капітал компанії в момент t, то розподіл Ut+h — Ut залежить лише від h і не залежить від t [4]. Ці обмеження є занадто жорсткими для нестаціонарних та неоднорідних портфелів, з якими працюють українські страховики.
Для врахування флуктуації розміру портфеля доцільно дослідити зміну кількості надходжень (внесків) впродовж різних часових інтервалів, тобто оцінити тип і параметри функції X(t). Рис. 2 відображає кількість внесків досліджуваної страхової компанії, одержаних упродовж календарного року, усереднену за 2000-2003 роки.
Дослідження флуктуацій розміру портфелів інших страхових компаній свідчить, що траєкторія кривої на рис. 2 є характерною для більшості компаній України, оскільки відображає основні закономірності процесу сплати внесків.
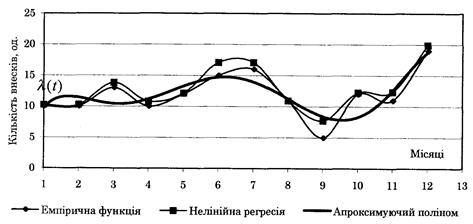
Рис. 5.1. Графік емпіричної функції інтенсивності для досліджуваної компанії та її апроксимація
Спостережувані коливання пояснюються як сезонними змінами, так і особливостями оподаткування прибутку страхувальників — суб'єктів підприємницької діяльності в Україні. Згідно ст. 5.4.6. Закону України «Про внесення змін до Закону України «Про оподаткування прибутку підприємств», будь-які витрати зі страхування майнових, кредитних та інших комерційних ризиків платника податку, відносяться до складу валових витрат платника, зменшуючи таким чином об'єкт оподатковування. Оскільки остаточний розрахунок і сплата податку на прибуток відбувається за результатами кварталу, то спостерігається чітка тенденція до різкого зростання кількості надходжень страхових внесків саме в останньому місяці кожного кварталу з піком у кінці календарного року. Враховуючи, що основними клієнтами страхових компаній є юридичні особи (на них припадає 90% страхових платежів), тенденція переростає в закономірність, характерну лише для українського страхового ринку.
Усі різкі спади і точки мінімумів функції X,(t) спричинені святковими періодами, періодами відпусток (січень, серпень-вересень) або співпадають із початком кварталу, коли кількість внесків після піку в кінці минулого кварталу суттєво зменшується.
Для врахування виявлених особливостей процесу надходження премій при моделюванні діяльності страхової компанії необхідно висунути гіпотезу про характер функціональної залежності A,(t) і апроксимувати її деяким математичним виразом шляхом регресійного та кореляційного аналізу.
Зважаючи на циклічні коливання емпіричної функції, знайдемо параметри апроксимуючого рівняння у формі гармонійних коливань:

Період о» знаходиться зі співвідношення юТ = 2я, зважаючи, що коливання відбуваються щоквартально:

Оцінка параметрів рівняння (3) методом найменших квадратів дала такий результат для досліджуваного страховика:


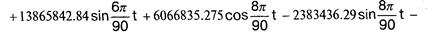

Коефіцієнт детермінації для даного наближення значно вищий, ніж для поліноміального: R2 = 0,952, що графічно підтверджує рис. 5.1 - емпірична і підібрана криві майже повністю співпадають.
Знайдену таким чином функціональну залежність A,(t) доцільно використовувати в моделюванні процесу надходження премій для врахування флуктуації розміру портфеля страховика впродовж різних часових інтервалів.
Отже, аналіз показує, що ймовірність появи принаймні одного клієнта в інтервалі [t, t + h] залежить не лише від довжини інтервалу h, але й від його положення на осі часу, і дорівнює A,(t)h + 0(h). Це уточнення дає підстави описувати процес надходження внесків неоднорідним пуассонівським процесом з функцією інтенсивності X(t).
Випадкові величини {('k,1 < k > n365}, які описують величину внесків за договорами страхування, є неперервними, незалежними і однаково розподіленими. Стохастична природа неперервної випадкової величини може бути описана функцією розподілу ймовірностей Fyk (х) = Р С^к - х) або щільністю розподілу ймовірностей fY|< (х) = Ру/ (х} якщо вона існує. Оскільки в нашому випадку величина Yk додатна, то Fyk (х) і fYk (х) тотожно дорівнюють нулеві для від'ємних значень х. Надалі вважатимемо, що х > 0..
Володіючи фактичними даними про розмір внесків, здійснених протягом деякого проміжку часу, можна отримати вибіркові оцінки середнього значення і дисперсії випадкової величини Yk — EYk і DYk відповідно. Виникає завдання підбору гіпотетичного розподілу FY (х), який із заданою точністю відповідає фактичним даним. Для цього використаємо метод моментів: підберемо теоретичний розподіл таким чином, щоб його моменти були близькі до моментів реальної статистики.
Побудова гістограм розподілу розмірів внесків для кількох десятків страхових компаній України дає змогу виявити певні особливості формування страхових портфелів, пов'язані з недостатнім рівнем розвитку страхового ринку. На рис. 5.2 наведено гістограму розподілу суми внесків для досліджуваної страхової компанії, за якою можна прослідкувати типові закономірності шуканого розподілу.

Рис. 5.2. Гістограма розподілу внесків для портфеля договорів досліджуваної страхової компанії
По-перше, одразу можна відзначити величезний розкид сум внесків (а відповідно і страхових сум) від кількох десятків до десятків тисяч гривень, що свідчить про те, що портфель складається з надзвичайно різнорідних ризиків без чіткої політики їхнього підбору. А саме на етапі відбору і класифікації ризиків (у процесі андерайтингу) закладається фундамент фінансової стійкості страховика. Практично жоден з елементів політики андерайтингу не розроблений належним чином і не застосовується в щоденній практиці прийому ризиків на страхування більшістю страховиків України, спричиняючи до неоднорідності портфеля. Як правило, лише за майновим страхуванням страховики спроможні укласти достатню кількість договорів для формування замкненої сукупності, в межах якої можна перерозподіляти збиток. В середньому договори майнового страхування становлять 60—90% усієї кількості договорів. За рештою видів страхування в портфелях компаній налічується незначна кількість угод (за винятком компаній, які спеціалізуються на певному виді страхування), при цьому страхові суми застрахованих об'єктів, а отже, і величина внесків за їхнє страхування, варіюються в дуже широких межах.
По-друге, візуальний аналіз отриманої гістограми дозволяє висунути гіпотезу про те, що на різних інтервалах суми внесків розподілені за різними законами розподілу. Підібрати криву щільності розподілу ймовірностей, яка б забезпечила задовільне наближення емпіричних і теоретичних даних на усьому проміжку від нуля до максимальної величини внеску не вдається. Статистичний аналіз гістограми дозволяє виділити кілька проміжків, в межах яких розміри внесків однаково розподілені. Зокрема, для гістограми на рис. З доцільно виділити три проміжки: (0; 13000], (13000; 42000], (42000; 60000]. Висунувши гіпотези про тип теоретичного розподілу випадкових величин на кожному з виділених інтервалів, необхідно оцінити параметри розподілів методом моментів або максимальної правдоподібності і визначити, з яким рівнем значимості гіпотеза про закон розподілу узгоджується з реальними даними. Графік інтегральної функції розподілу FYk (х) на проміжку (0; 60 000] (рис. 4) складатиметься з трьох частин, при цьому
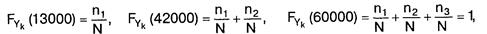
де ПІ5 П2, П3 - середня кількість спостережуваних значень величини Yk на проміжках (0; 13000], (13000; 42000], (42000; 60000] відповідно; N -загальна кількість спостережуваних значень випадкової величини Yk.
Перший крок - перевірка гіпотези про закон розподілу випадкової величини Yk на інтервалі (0; 13000]. За вибіркою значень величини внесків на цьому інтервалі та заданим рівнем значимості необхідно прийняти або відхилити гіпотезу: генеральна сукупність має гама-роз-поділ з параметрами А, > 0 і а > 0, тобто:

де Г - гама-функція,


Рис. 5.3. Інтегральна функція розподілу суми внесків на проміжку (О; 60000]
При знаходженні функції розподілу необхідно врахувати, що неперервна величина Yk має гама-розподіл лише на інтервалі (0; 13000], причому площа під кривою щільності розподілу на даному інтервалі відповідатиме ймовірності попадання випадкової величини в цей проміжок, тобто

Звідси можна знайти нормуючий коефіцієнт k, для функції щільності розподілу:

методом моментів знайдемо незміщені, істотні точкові оцінки параметрів гама-розподілу:

Для досліджуваної страхової компанії EY = 2756,88 грн., DYk = 15089575 грн., а = 0,50368, Я = 0,0001827.
Перевіримо гіпотезу про закон розподілу за критерієм -£ Пірсона. Оскільки розрахункова величина *£ = 11,21 є меншою від критичного табличного значенням хр2 = 11,29 для рівня значимості 0,02 і 23 (k - s - 1 = 26 -2 - 1 = 23) ступенів свободи, то з ймовірністю 98% на проміжку (0; 13000] емпіричний розподіл випадкової величини Yk відповідає теоретичному гама-розподілу [3]. Цей висновок дає підстави використовувати нормований гама-розподіл для моделювання величини внесків досліджуваної страхової компанії на інтервалі (0; 13000].
З гістограми (рис. 3) видно, що на інтервалі (13000; 42000) з'являються нові сплески відносних частот, які вже не можна пояснити гама-розподіл ом. Оскільки процес їхнього загасання доволі тривалий, то для апроксимації випадкової величини Yk на цьому проміжку доцільно застосовувати розподіли з «важкими хвостами». Висунемо гіпотезу про те, що, якщо початок проміжку (13000; 42000) змістити до нуля, то спостережувані на ньому значення величини Yk мають розподіл Парето з параметрами ц > 0 і (3 > 0, тобто

Для цього розподілу коефіцієнт варіації завжди більший від одиниці, що вказує на досить високу ймовірність появи великих сум внесків.
Необхідно знайти точкові оцінки параметрів зміщеного розподілу Парето FYk (х - х0; ц\ р), нормованого за допомогою коефіцієнта k2, виходячи з рівняння:
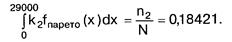
За допомогою методу максимальної правдоподібності знайдемо оцінки параметрів розподілу Парето, максимізувавши логарифм функції:

В результаті обчислень одержуємо, що для досліджуваної страхової компанії: р = 102, ц = 1084462,09.
Співставляючи спостережувані відносні частоти і теоретичні ймовірності, знаходимо, що статистика х2 = 4,03. Оскільки розрахункова статистика є меншою від табличного значення %р2 = 4,18 для рівня значимості 0,02 i!2(k-5-1 = 15-2-1 = 12) ступенів свободи, то з ймовірністю 98% можна стверджувати, що немає суттєвих розходжень між спостережуваними даними на проміжку (13000; 42000) і очікуваними даними, які одержані з розподілу Парето з параметрами Р = 102, ц = 1084462,09 [3]. Цей висновок підтверджує гістограма на рис. 5.
Візуальний аналіз частот появи великих значень випадкової величини Yk (рис. 3) дозволяє висунути гіпотезу про рівномірний розподіл величини внесків, які перевищують 42 тис. грн., тобто на проміжку [42000; 60000] з однаково малою ймовірністю можна очікувати появи будь-якого значення величини Yk. Це пов'язано з тим, що при страхуванні об'єктів, страхові суми за якими перевищують 500 тис. грн., застосовується індивідуальний підхід до розрахунку страхових тарифів.

Перевіримо гіпотезу про те, що функція розподілу випадкової величини Yk на проміжку [42000; 60000] має вигляд:
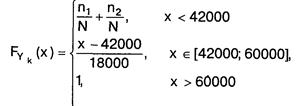
а щільність розподілу - нормована:


Для математичного обґрунтування вибору на користь даного розподілу застосуємо критерій Колмогорова-Смірнова, оскільки обсяг значень вибірки на інтервалі [42000; 60000] є невеликим, що знижує достовірність критерію І\ За таблицею критичних чисел Колмогорова-Смірнова знаходимо Окрит = 0,27 для обсягу вибірки 35 і а = 0,01. Порівнюючи найбільшу абсолютну різницю між спостережуваними і
теоретичними значеннями (0,19) з Окрит: Оемп < Окрит, робимо висновок, що експериментальний розподіл — рівномірний.
З метою перевірки адекватності підбору кількох теоретичних розподілів для моделювання величини внесків доцільно обчислити статистику X2 для усіх значень відносних частот і нормованих теоретичних ймовірностей на інтервалі (0; 60 000), враховуючи, що
k, = 0,729561788, К2 = 0,19763066, k3 = 0,11699064.
Оскільки розрахункова статистика %2 = 16,14 є меншою від табличного значення %р2 = 16,31 для рівня значимості 0,02 і ЗО ступенів свободи, то з ймовірністю 98% можна стверджувати, що немає суттєвих розходжень між спостережуваними і очікуваними даними, які одержані з гама-розподілу, розподілу Парето та рівномірного розподілу.
Висновок. Підібрані теоретичні розподіли для опису процесу надходження премій дають змогу відтворити цей процес у динаміці з метою вивчення його впливу на динамічну платоспроможність страхової компанії. Це досягається шляхом співставлення процесу надходження з паралельним стохастичним процесом виплати страхових відшкоду-вань, який також характеризується стаціонарністю, ординарністю та відсутністю післядії, тобто має пуассонівські властивості.
Наведена методика базується на загальних закономірностях процесу надходження страхових внесків, виявлених для українського страхового ринку, однак в процесі моделювання тип і параметри теоретичних розподілів повинні визначатися на основі емпіричних даних конкретної страхової компанії.






