Головними проблемами, що виникають при запровадженні нового виду страхових послуг, є проблеми оптимізації: процесу надходжень страхових платежів; процесу формування та розміщення страхових резервів; процесу подальшого розподілення ризиків; процесу компенсації здійснених страхових відшкодувань. Концепцію стратегії страхової компанії представлено на рис. 4.1 як сукупність стратегічних інтересів, функцій компанії, використовуваних функціональних механізмів, а також математичних інструментів та інструментів автоматизованого управління, які використовуються для досягнення цілей існування та розвитку компанії.

Рис.1. Концепція оптимальної стратегії страхової компанії
Страхова компанія розглядається як динамічна система  , при цьому:
, при цьому:
 , (1)
, (1)
де  - підсистеми системи “Страхова компанія”, які відповідають функціональним особливостям стратегії в різних сферах діяльності:
- підсистеми системи “Страхова компанія”, які відповідають функціональним особливостям стратегії в різних сферах діяльності: 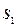 – область впровадження виду страхування (відповідає діям страхової компанії, які супроводжують процес впровадження страховою компанією виду страхування);
– область впровадження виду страхування (відповідає діям страхової компанії, які супроводжують процес впровадження страховою компанією виду страхування);  – область накопичення (відповідає діям страхової компанії щодо управління страховим портфелем, а також процесу розміщення страхових резервів);
– область накопичення (відповідає діям страхової компанії щодо управління страховим портфелем, а також процесу розміщення страхових резервів);  – область виплат (відповідає діям страхової компанії, пов'язаним із проведенням страхових виплат у зв'язку із здійсненням страхових виплат за страховими випадками, що настали).
– область виплат (відповідає діям страхової компанії, пов'язаним із проведенням страхових виплат у зв'язку із здійсненням страхових виплат за страховими випадками, що настали).
При цьому з підсистеми  страхувальник може перейти лише до підсистеми
страхувальник може перейти лише до підсистеми  , а перехід з підсистеми
, а перехід з підсистеми  до області
до області  носить циклічний характер і питання цього переходу регулюються лише різними часовими відрізками.
носить циклічний характер і питання цього переходу регулюються лише різними часовими відрізками.
 – множина станів системи “Страхова компанія”. Характеризується лінгвістичною змінною: wi Î[“Стан мінімального ризику для виду страхування”, “Стан припустимого ризику для виду страхування”, “Стан підвищеного ризику для виду страхування”, “Стан катастрофічного ризику для виду страхування”, “Стан підвищеного ризику для страхової компанії”, “Стан катастрофічного ризику для страхової компанії”].
– множина станів системи “Страхова компанія”. Характеризується лінгвістичною змінною: wi Î[“Стан мінімального ризику для виду страхування”, “Стан припустимого ризику для виду страхування”, “Стан підвищеного ризику для виду страхування”, “Стан катастрофічного ризику для виду страхування”, “Стан підвищеного ризику для страхової компанії”, “Стан катастрофічного ризику для страхової компанії”].
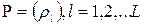 – множина ризиків, які характеризують діяльність страхової компанії.
– множина ризиків, які характеризують діяльність страхової компанії.
 – множина дестабілізуючих впливів ризику
– множина дестабілізуючих впливів ризику  таких, що здатні перевести систему
таких, що здатні перевести систему  зі стану
зі стану  до стану
до стану  в момент функціонування підсистеми
в момент функціонування підсистеми  .
.
 – множина керуючих команд (стабілізуючих сигналів), які виробляє система-координатор для того, щоб перевести себе із стану
– множина керуючих команд (стабілізуючих сигналів), які виробляє система-координатор для того, щоб перевести себе із стану  до стану
до стану  при функціонуванні підсистеми
при функціонуванні підсистеми  , для можливості функціонування підсистеми
, для можливості функціонування підсистеми  .
.
Керуюча команда має давати відповідь на питання, яким шляхом має здійснюватись попередження або ліквідація ризику – шляхом передачі ризику, контролю за ризиком або фінансування ризику.
Загальну схему управління ризиком страхової компанії наведено на рис.4.2.
Величина 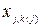 , через яку описується змінна
, через яку описується змінна  , визначається як інтегрований показник загальної суми ризику, що застерігає страхову компанію в окремий момент часу. Він розраховується таким чином:
, визначається як інтегрований показник загальної суми ризику, що застерігає страхову компанію в окремий момент часу. Він розраховується таким чином:
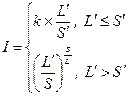 , (2)
, (2)
де  – відношення резервів по виду страхування до загальної суми страхових резервів;
– відношення резервів по виду страхування до загальної суми страхових резервів;  – сума резервів по виду страхування;
– сума резервів по виду страхування;  – загальна сума страхових резервів;
– загальна сума страхових резервів;  - сума, яка підлягає виплаті при настанні страхового випадку;
- сума, яка підлягає виплаті при настанні страхового випадку;  – страхова сума за договором страхування;
– страхова сума за договором страхування;  – коефіцієнт залежності (використовується в зв’язку з наявністю зворотної залежності між ймовірністю настання страхового випадку та сумою страхової виплати);
– коефіцієнт залежності (використовується в зв’язку з наявністю зворотної залежності між ймовірністю настання страхового випадку та сумою страхової виплати);  – ймовірність того, що настане страховий випадок, який охоплює декілька груп ризиків;
– ймовірність того, що настане страховий випадок, який охоплює декілька груп ризиків;  – групи ризиків,
– групи ризиків,  ;
;  – літеральні змінні, які характеризують групи страхового ризику (ризики, які пов’язані із причиненням шкоди майну; ризики відповідальності; ризики неотримання прибутку).
– літеральні змінні, які характеризують групи страхового ризику (ризики, які пов’язані із причиненням шкоди майну; ризики відповідальності; ризики неотримання прибутку).

Рис.4.2. Схема ризикового управління страховою компанією
Враховуючи, що серед факторів, які значним чином впливають на визначення ймовірності настання страхового випадку, а відповідно – й розміру страхового тарифу є вплив ступеня зносу застрахованого об’єкту, запропоновано метод адаптації страхового тарифу до ступеня зношеності основних фондів.
При цьому значення ризику виникнення страхового випадку протягом періоду корисного використання основних фондів визначається ступеневою функцією  , а сума накопиченої амортизації визначається логарифмічною або лінійною функцією
, а сума накопиченої амортизації визначається логарифмічною або лінійною функцією  .
.
Функції  та
та  перетинаються при значенні y, яке дорівнює 1. Параметри функції
перетинаються при значенні y, яке дорівнює 1. Параметри функції  задано таким чином, щоб значення функції набувало значення 1 при параметрі t, який забезпечує рівень амортизації, що дорівнює 1.
задано таким чином, щоб значення функції набувало значення 1 при параметрі t, який забезпечує рівень амортизації, що дорівнює 1.
На всьому інтервалі [0;t] рівень зношеності є більшим за середньостатистичний рівень ризику (ризик є нееластичним від рівня амортизації).
Крім того, в моделі використовується функція  , яка є “песимістичною” функцією розподілу ризику та перетинається із функцією
, яка є “песимістичною” функцією розподілу ризику та перетинається із функцією  в момент t1 (обидві функції при цьому мають значення k). Під час наближення до цього моменту можна говорити про те, що ризик техногенної катастрофи дорівнює рівню зношеності (який визначено змінною k). Після цього моменту незначне зростання рівня зношеності призводить до значного зростання ризику (ризик стає еластичним до рівня амортизації).
в момент t1 (обидві функції при цьому мають значення k). Під час наближення до цього моменту можна говорити про те, що ризик техногенної катастрофи дорівнює рівню зношеності (який визначено змінною k). Після цього моменту незначне зростання рівня зношеності призводить до значного зростання ризику (ризик стає еластичним до рівня амортизації).
Функція  досягає значення 1 вже в момент t2, після якого страхування стає фактично недоцільним для страховика.
досягає значення 1 вже в момент t2, після якого страхування стає фактично недоцільним для страховика.
З урахуванням наведених обставин “гнучкість” страхового тарифу має забезпечуватись формулою:
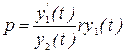 ,
,  , (3)
, (3)
де p – страховий тариф; r – нетто-ставка, обчислена за принципами актуарної математики.
Зазначений метод дозволяє оптимізувати розмір страхового тарифу таким чином, щоб він найбільш повно відображав ризиковість страхування і водночас був достатньо конкурентним.
Не останню роль у моделюванні оптимальної стратегії страхової компанії відіграє моделювання системи розподілу ризику. Умови ринкової конкурентної рівноваги передбачають “справедливий” розподіл попиту між страховиками, це обумовлює той факт, що кожен страховик має прийняти на себе лише таку частку ризику, яку може фактично забезпечити. В зв’язку з цим виникає необхідність перестрахування, тобто передачі надлишкової частки ризику страховику, який може прийняти її. Для прийняття оптимального рішення про перестрахування будемо використовувати модель справедливого перестрахування, яку наведено нижче.
Страховик 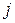 має страхові резерви
має страхові резерви  та частку загального ринку
та частку загального ринку  . При цьому
. При цьому  виражає собою частку чистих зобов’язань, тобто різницю між зобов‘язаннями, що прийнято, та зобов’язаннями, які передано в перестрахування.
виражає собою частку чистих зобов’язань, тобто різницю між зобов‘язаннями, що прийнято, та зобов’язаннями, які передано в перестрахування.
Нехай  є часткою сукупного ризику, що прийнято на страхування
є часткою сукупного ризику, що прийнято на страхування 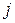 -м страховиком (
-м страховиком ( ), а
), а  – частку сукупного ризику, яку страховик
– частку сукупного ризику, яку страховик 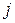 перестраховує (
перестраховує ( ). Якщо
). Якщо  , страховик поступається частиною страхового портфелю шляхом укладання договору перестрахування. Якщо
, страховик поступається частиною страхового портфелю шляхом укладання договору перестрахування. Якщо  – страховик приймає на себе перестрахування. Чиста гарантія таким чином представляє собою
– страховик приймає на себе перестрахування. Чиста гарантія таким чином представляє собою  . Якщо опустити індекс
. Якщо опустити індекс 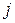 , функція, яка максимізується, виглядає так:
, функція, яка максимізується, виглядає так:
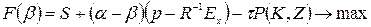 , (4)
, (4)
де  ,
,  ,
,  ;
;  – рентабельність;
– рентабельність;  – очікуване значення сукупних страхових відшкодувань;
– очікуване значення сукупних страхових відшкодувань;  – сукупне страхове відшкодування;
– сукупне страхове відшкодування;  – конкурентний ринковий тариф.
– конкурентний ринковий тариф.
Обмеження моделі в цьому випадку виглядають таким чином:
1.  , (5)
, (5)
де 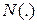 – стандартна нормальна функція розподілу;
– стандартна нормальна функція розподілу;  – стандартна нормальна функція щільності;
– стандартна нормальна функція щільності;  ;
;  – страхові відшкодування;
– страхові відшкодування; 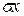 – середньоквадратичне відхилення сукупного страхового відшкодування.
– середньоквадратичне відхилення сукупного страхового відшкодування.
2.  . (6)
. (6)
|
 , (7)
, (7)
 ,
,
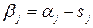 .
.
Реалізація зазначеної моделі дозволяє визначити розміри зобов’язань, які належать кожному перестраховику в умовах ринкової рівноваги.
Для реалізації моделі оптимальної поведінки страхової компанії використано метод ймовірнісно-автоматного моделювання, оскільки він найбільш вдало забезпечує імітацію реального функціонування компанії. Логіка побудови зазначеної моделі передбачає, що стабілізація стану страхової компанії здійснюється за рахунок підбору оптимальних значень змінних  (частота генерації стабілізуючого сигналу системою-координатором) та
(частота генерації стабілізуючого сигналу системою-координатором) та  (чутливість страхових резервів до стабілізуючого сигналу).
(чутливість страхових резервів до стабілізуючого сигналу).
Для досягнення мети запропоновано використати варіант загальновідомої задачі оптимальної виробничої програми.
В такому випадку цільова функція моделі буде виглядати таким чином:
 . (8)
. (8)
Задачу максимізації цільової функції вирішено за умови дотримання таких обмежень:
 ,
,
 ,
,
 ,
,
де 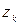 – матриця обмежень компанії по ресурсам
– матриця обмежень компанії по ресурсам  – го виду;
– го виду;  – множина заходів страхової компанії, які можуть бути вжиті для зміни фінансового стану;
– множина заходів страхової компанії, які можуть бути вжиті для зміни фінансового стану;  – інтенсивність застосування відповідних заходів;
– інтенсивність застосування відповідних заходів;  – множина ресурсів, які має компанія;
– множина ресурсів, які має компанія; 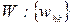 – матриця витрат ресурсу
– матриця витрат ресурсу  при застосуванні заходів
при застосуванні заходів  з одиничною інтенсивністю;
з одиничною інтенсивністю;  – інтегрований показник фінансового стану страхової компанії в поточний момент;
– інтегрований показник фінансового стану страхової компанії в поточний момент;  – інтегрований показник фінансового стану страхової компанії внаслідок реалізації заходів
– інтегрований показник фінансового стану страхової компанії внаслідок реалізації заходів  з інтенсивністю
з інтенсивністю  .
.
В результаті вирішення задачі отримано значення, необхідні для реалізації моделі.
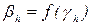 , (9)
, (9)
 ,
,
де  – матриця приросту ресурсів
– матриця приросту ресурсів  - го виду в разі вжиття заходів виду
- го виду в разі вжиття заходів виду  .
.
Вирішення цієї задачі здійснюється з урахуванням того, що матриця обмежень 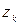 може приймати різні значення залежно від того, в якому фінансовому стані знаходиться страхова компанія на поточний момент.
може приймати різні значення залежно від того, в якому фінансовому стані знаходиться страхова компанія на поточний момент.
Слід зазначити, що залежно від визначення стану страхової компанії, тобто від того, який набір обмежень 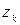 буде використано, буде залежати надалі стратегія страхової компанії, а також ризик її реалізації. При більш нестабільному стані страхової компанії набір обмежень буде найбільш жорстким, при менш нестабільному стані – менш жорсткий. Проте в зв’язку з тим, що фінансовий стан страхової компанії визначається нечіткою змінною, є певний ризик, до якого може бути схильна компанія в разі вибору стратегії, яка не відповідає реальному фінансовому стану.
буде використано, буде залежати надалі стратегія страхової компанії, а також ризик її реалізації. При більш нестабільному стані страхової компанії набір обмежень буде найбільш жорстким, при менш нестабільному стані – менш жорсткий. Проте в зв’язку з тим, що фінансовий стан страхової компанії визначається нечіткою змінною, є певний ризик, до якого може бути схильна компанія в разі вибору стратегії, яка не відповідає реальному фінансовому стану.
Таким чином, для вибору оптимальної поведінки страхової компанії (що забезпечується опосередковано через вибір набору обмежень 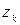 ) необхідно використовувати такі критерії:
) необхідно використовувати такі критерії:
 , (10)
, (10)
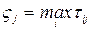 , (11)
, (11)
 , (12)
, (12)
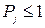 , (13)
, (13)
 , (14)
, (14)
 , (15)
, (15)
 , (16)
, (16)
де 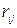 – ризик при прийнятті
– ризик при прийнятті  -го рішення (виборі
-го рішення (виборі  -го набору обмежень) та виникненні
-го набору обмежень) та виникненні 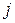 -х умов;
-х умов;  – ймовірність настання
– ймовірність настання 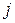 -х умов;
-х умов;  – виграш при прийнятті
– виграш при прийнятті  -го рішення та виникненні
-го рішення та виникненні 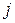 -х умов;
-х умов;  – максимальний виграш при виникненні
– максимальний виграш при виникненні 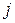 -х умов;
-х умов;  – кількість рішень;
– кількість рішень;  – кількість умов.
– кількість умов.
Для обґрунтування заходів, які вживаються для вибору управлінських рішень в умовах невизначеності обставин, використано такі критерії.
Критерій, побудований на відомих ймовірностях ( ):
):
 ,
,  , (17)
, (17)
де 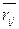 - середнє значення ризику (математичне сподівання ризику).
- середнє значення ризику (математичне сподівання ризику).
Крім вказаного критерію, в залежності від конкретної ситуації, є можливим використання принципу недостатнього обґрунтування Лапласа, максимального критерію Вальда, мінімального критерію Севіджа та критерію узагальненого максиміну (песимізму-оптимізму) Гурвіца.
Загальну схему алгоритму прийняття управлінських рішень в ризикових та невизначених ситуаціях наведено на рис. 4.3.

Рис. 4.3. Алгоритм прийняття управлінського рішення в системі управління страховою компанією
Алгоритм розрахунку є точним уявленням, яке дозволяє за допомогою певної кількості послідовних кроків отримати бажаний результат (рішення) на підставі заданих інформаційних даних. Сутність складання алгоритму полягає в послідовному розкладенні обчислювального процесу (операцій) на складові частини, які визначають оптимальність рішень.
У випадку, якщо фінансовий стан компанії можна визначити з функцією приналежності, яка наближається до одиниці, оптимальне рішення визначається за формулами (10)-(17). Такі самі критерії використовуються, якщо функція приналежності до одного стану значно (більш, ніж в 4 рази) перевищує значення функції приналежності до іншого фінансового стану. Результатом виконаних дій є отримання переліку оптимальних рішень.
У випадку, якщо функції приналежності до різних станів страхової компанії не відрізняються значно, вибирається один з критеріїв визначення оптимального рішення. Аналіз та оцінка ступеня ризику при виборі критерію здійснюється на підставі результатів господарської діяльності та особистого досвіду керівника, який приймає рішення, а також його схильності до ризику, можливих обставин та ліміту часу, який необхідний для прийняття рішення.







