1. Собственная размерность. Конечные элементы могут описываться одной, двумя или тремя пространственными координатами в зависимости от размерности задачи, для решения которой они предназначены. Соответствующее число внутренних или локальных координат называется собственной размерностью элемента. В расчетах могут использоваться также специальные элементы с нулевой размерностью, такие как, точечные массы или сосредоточенные упругие элементы (пружины).
2. Узловые точки. Каждый элемент описывается множеством характерных точек, называемых узловыми точками или узлами.
3. Геометрия элемента. Геометрия элемента определяется расположением узловых точек. Большинство элементов, используемых в расчетах, имеют достаточно простую геометрическую форму. Например, в одномерном случае элементы обычно представляют собой прямолинейные отрезки или сегменты кривых линий; в двумерном случае элементы имеют трехстороннюю или четырехстороннюю форму; в трехмерных задачах наиболее распространены такие геометрические фигуры, как тетраэдры, призмы и гексаэдры (Рис. 8).

Рис. 8. Основные типы конечных элементов для одно-, дву- и трехмерных задач механики.
4. Степени свободы. Степени свободы определяют физическое состояние элемента. Благодаря общим степеням свободы в соседних элементах осуществляется сборка модели и формирование глобальной системы конечно-элементных уравнений.
5. Узловые силы. Система узловых сил полностью соответствует степеням свободы элемента и выражается с помощью глобального вектора узловых сил.
6. Определяющие соотношения. Для конечных элементов, используемых в механических расчетах, определяющее соотношение задает поведение материала, из которого изготовлена конструкция. Например, в качестве такого соотношения во многих случаях используется обобщенный закон Гука, связывающий тензор деформаций и тензор напряжений в точке. Для линейного упругого стержневого элемента достаточно задать один модуль Юнга Е и один коэффициент температурного расширения.
7. Свойства сечения. К свойствам сечения относятся площади и моменты инерции одномерных и двумерных конечных элементов, таких как балки, стержни, пластины. В эту группу также входит толщина пластин и оболочек. При построении конечного элемента свойства сечений считаются заданными и входят в результирующую матрицу жесткости элемента.
Например, при решении плоских задач стержневые элементы могут быть только трех типов:
· Шарнирно опертый стержневой элемент;
· Балочный элемент, жестко защемленный по обоим концам;
· Комбинированный элемент (шарнир на одном конце и заделка на другом).
Особенности МКЭ.
Принципиальная особенность МКЭ заключается в том, что в этом методе невозможно пренебречь осевыми деформациями.
В МКЭ при построении матриц жесткости удовлетворяются условия равновесия (матрица А), физические уравнения (матрица K), уравнение неразрывности (условие B = AT).
Для пластин, оболочек и объемных элементов действуют те же принципы. Конечными элементами для таких систем служат чаще всего треугольные и прямоугольные элементы (поскольку гораздо проще смоделировать поверхность криволинейной формы большим числом прямолинейных элементов, чем вводить в расчет специальные криволинейные элементы). Для объемных задач используются параллелепипеды призмы и тетраэдры.
Кроме того, в некоторых случаях разными конечно-элементными программами используются т.н. специальные элементы. Специальные элементы выводятся из уравнений механики сплошной среды, но включают в себя некоторые особенности, непосредственно связанные с физическими особенностями решаемых задач. В качестве примера можно привести следующие специальные элементы: элемент с трещиной для задач механики разрушения; многослойная панель; бесконечные и полубесконечные элементы; контактные и штрафные элементы; абсолютно твердотельные элементы, элементы типа «ребро», «трос».

Рис.9. Специальные конечные элементы.
МКЭ является приближенным методом. Его точность зависит от числа конечных элементов. В последнее время наблюдается тенденция к упрощению системы моделирования. В этом случае элемент по умолчанию принимается с наибольшим числом степеней свободы, а ограничения накладываются на него автоматически.
Сравнительная таблица алгоритмов ММП и МКЭ
| ММП | МКЭ |
| 1. Строятся вручную исходные матрицы А, k, векторы P, S0 | 1. Вводятся в машину координаты узлов Xi, Yi. Задаются элементы по соответствующим узлам и их жесткости E, F, I, а также внешние воздействия: нагрузки температурные воздействия осадки опор. |
| 2. Вычисляется матрица усилий k·AT и матрица жесткости конструкции K = A·k·AT. | 2. Компьютер по стандартному алгоритму вычисляет матрицы усилий (k·AT)Э, матрицы жесткости KЭ = (A·k·AT)Э и записывает их на жесткий диск. |
| 3. Решается системы уравнений K·Z = P, из нее находится вектор Z. | 3. Составляется матрица жесткости всей системы:  . .
|
| 4. Определяются расчетные усилия S = k·AT·Z | 4. Решается системы уравнений K·Z = P. |
| 5. Добавляются усилия от внеузловой нагрузки S = S + S0 | 5. Находятся усилия во всех элементах 
|
| 6. Добавляются усилия от внеузловой нагрузки S = S + S0 |
Главное отличие ММП от МКЭ в том, что ММП матрицы жесткости строятся вручную для каждой новой конструкции, а в МКЭ глобальная матрица жесткости конструкции получается простым суммированием по определенному правилу матриц жесткости всех элементов, вычисленных по стандартным алгоритмам, заложенным в машине.
1.3.3 Порядок подготовки и ввода исходных данных для МКЭ:
1. Завести все узлы конструкций по координатам;
2. Ввести элементы по начальному узлу i и конечному узлу j (в некоторых программах пункты 1 и 2 объединены в одну операцию). В некоторых программах может задаваться также 3-й узел k, определяющий ориентацию местных осей элемента. (Ось 1 элемента направлена от начального узла к конечному, ось 2 лежит в плоскости i-j-k, а ось 3 перпендикулярно ей)
В большинстве программ местные оси элементов задаются программой автоматически по определенным правилам.
Местные оси элементов.
Компьютерные программы, работающих с МКЭ, обычно оперируют с несколькими системами координат. Минимально их может быть две:
- Глобальная система координат (ГСК) служит для описания координат узлов, определения направления степеней свободы, вывода перемещений узлов, для задания локальных систем координат. Глобальная система координат в проекте может быть только одна, и ее ориентацию нельзя изменить.
- Местные (локальные) системы координат (МСК или ЛСК). Они определяют направление действия некоторых нагрузок, ориентацию жесткостных характеристик в пространстве, и соответственно направление усилий или напряжений в элементе. Локальных систем координат может быть больше одной, и они могут задаваться пользователем для удобства ввода данных или чтения результатов. Кроме того существует местная система координат (как частный случай локальной) жестко связанная с элементом. Для каждого элемента может быть только одна местная система координат. Она задается программой автоматически «по умолчанию» для каждого типа элемента, но пользователь при необходимости может поменять ее ориентацию.
После этого программа автоматически определяет геометрические характеристики элемента:

3. Задать жесткостные характеристики элемента:
E – модуль упругости;
F – площадь поперечного сечения;
I – момент инерции относительно соответствующей локальной оси.
Для упрощения работы пользователя большинством программ вводятся специальные библиотеки стандартных сечений, т.е. сечений, жесткости которых вычисляются автоматически по задаваемым пользователем параметрам.
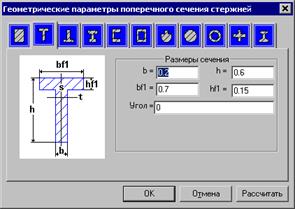
Рис. 10 Пример библиотеки стандартных сечений железобетонных элементов.
Задаются узловые силы и узловые моменты, а также внеузловая нагрузка которая приводит узловую нагрузку к узловой.
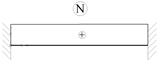
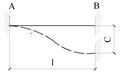
Таблица приведения внеузловой нагрузки к узловым усилиям
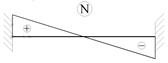
| № | Тип нагрузки | Эпюра усилий | Значения узловых сил и моментов |

| 
| 
| |

| 
| 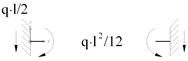
| |

| 
| 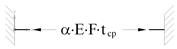
| |

| 
| 
| |
| 5[3] | 
| 
| 
|

| 
| 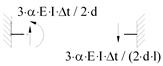
| |

| 
| 
| |

| 
| 
| |
| 
| 
|
1.3.4 Матрицы жесткости типовых стержневых элементов (плоская задача):






