Компоненты оптимального решения двойственной задачи называются оптимальными (двойственными) оценками прямой задачи. Академик Л.В. Канторович назвал их объективно обусловленными оценками.
Для выяснения смысла этих оценок вернемся к задаче об использовании ресурсов из п. 5.3. Требуется:
1) определить оптимальный план производства двух видов изделий, максимизирующий прибыль;
2) определить дефицитность сырья;
3) оценить целесообразность введения в план производства фирмы нового вида изделий (четвертого), нормы затрат на единицу которого, соответственно равны 1, 2, 2, а прибыль составляет 4,5 тыс. руб.
4) установить границы распределения ресурсов, при которых номенклатура выпускаемой продукции будет соответствовать оптимальному плану;
5) установить в каких пределах можно изменять цену продукции, чтобы при этом сохранить оптимальный план выпуска;
6) установить размеры максимальной прибыли при изменении запасов сырья на 2 т, количества оборудования – на 1 ед., объемов электроэнергии – на 2 ГВт. Оценить раздельное влияние этих изменений и суммарное их влияние на прибыль;
7) определить величину ∆ b1 первого ресурса, введением которого в производство можно компенсировать убыток и сохранить максимальный доход на прежнем уровне (ресурсы предполагаются взаимно заменяемыми), получаемый при исключении из производства ∆ b2 = 2 ед. второго ресурса, что вызывает уменьшение максимального дохода.
8) оценить целесообразность приобретения ∆ b2 = 1 единицы второго ресурса по цене сk = 2 тыс. руб. за единицу.
Основные переменные прямой задачи x1, x2 отражают оптимальный план производства продукции. Основные переменные двойственной задачи y1, y2, y3 представляют собой оценки ресурсов (теневые, скрытые цены ресурсов). Дополнительные переменные прямой задачи x3, x4, x5 согласно выражению (7.12) представляют собой разность между запасами bi ресурсов и их потреблением и выражают остатки ресурсов, а дополнительные переменные двойственной задачи y4, y5 согласно выражению (7.13) представляют разность между затратами на ресурсы для производства из них единицы продукции и ценами cj продукции и выражают превышение затрат над ценой:
| Компоненты оптимального решения прямой задачи I | ||||
| План производства | Остатки ресурсов, единиц | |||
| 
| 
| 
| 
|
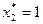
| Превышение затрат на ресурсы над ценой реализации (возможный убыток от производства продукции) | Объективно обусловленные оценки ресурсов (теневые, условные, скрытые цены ресурсов) | |||
| Компоненты оптимального решения двойственной задачи II | ||||
1. В оптимальный план производства следует включить оба вида продукции (, ).
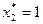2. Ресурсы b1 и b2 по оптимальному плану полностью использованы (, ), в объективно обусловленные оценки этих ресурсов ненулевые (, ). Ресурс b3 не полностью используется в оптимальном плане () и объективно обусловленная оценка этого ресурса нулевая ().
Таким образом, объективно используемые оценки ресурсов определяют степень дефицитности ресурсов, т.е. в оптимальном плане производства дефицитные (т.е. полностью используемые) ресурсы получают ненулевые оценки, а недефицитные – нулевые оценки.
Если 
, то при увеличении i -го ресурса оптимальный доход останется неизменным и ценность этого ресурса равна нулю. Действительно, сырье, запасы которого превышают потребность в нем, не представляет ценности для производства и его оценку можно принять за ноль.
Если 
велико, то незначительному увеличению i -го ресурса будет соответствовать существенное увеличение оптимального дохода, и ценность ресурса высока. Уменьшение ресурса ведет к существенному сокращению выпуска продукции.
считают некоторой характеристикой ценности i -го ресурса. В частности, при увеличении i -го ресурса на единицу (D bi = 1) оптимальный доход возрастает на , что позволяет рассматривать как условную цену, оценку единицы i -го ресурса, объективно обусловленную оценку.
По оптимальному плану в прямой задаче следует производить оба вида продукции (, 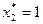), и превышение затрат на ресурсы над ценой реализации равно нулю (, ). Если бы затраты на ресурсы превышали цену изготавливаемой из них продукции, например, продукции второго вида, т.е. если бы 
, то на основании теоремы 2 оптимальное решение, соответствующей переменной 
, и в этом случае по оптимальному плану производить продукцию второго вида не следует.
Таким образом, в оптимальный план производства могут попасть только рентабельные (неубыточные) виды продукции при условии, что критерий рентабельности состоит в том, что цена продукции не превышает затрат на потребляемые при ее изготовлении материально-сырьевые ресурсы.
3. Для оценки целесообразности введения в план производства фирмы нового вида изделий (третьего), нормы затрат на единицу которого, соответственно равны 1, 2, 2, а прибыль составляет 4,5 тыс. руб. используем объективно обусловленные оценки ресурсов.
Если соотношение дополнительных затрат и цены реализации дополнительного вида продукции удовлетворяет следующему условию
, (7.16)
то включение дополнительного вида продукции n+1 в план производства целесообразно.
Расчет затрат осуществим по формуле
тыс. руб.
Учитывая, что затраты на продукцию третьего вида выше цены реализации с3 = 4,5 тыс. руб., то включение ее в план производства нецелесообразно.
4. С помощью оптимального решения двойственной задачи можно определить степень влияния ограничений на значение целевой функции.
Вернемся к решению задачи из п. 5.3, в последнюю таблицу добавим строку с обозначением двойственных переменных:
| сi | БП | 
| |||||
| х1 | х2 | х3 | х4 | х5 | bi | ||
| x2 | -1 | ||||||
| x1 | -1 | ||||||
| x5 | -3 | ||||||
| D j | |||||||
| уj | у4 | у5 | у1 | у2 | у3 |
Из последней таблицы симплекс-метода составим систему неравенств, отражающую возможность изменения ресурса i -го вида на величину D bi исходя из требования сохранения условия неотрицательности переменных прямой задачи.
Для исследования границ изменения первого вида ресурса имеем:
Þ 
Þ 
.
Учитывая, что b1 = 4, допустимый интервал изменения границ первого вида ресурса составит 
или 
.
Аналогично, определяем допустимый интервал изменения границ второго вида ресурса:
Þ 
Þ 
.
Учитывая, что b2 = 3, допустимый интервал изменения границ второго вида ресурса составит 
или 
.
Третий ресурс не является дефицитным:
Þ 
Þ 
.
Учитывая, что b3 = 8, допустимый интервал изменения границ третьего вида ресурса составит 
или 
.
5. Для оценки пределов возможного изменения цен продукции при условии сохранения оптимального плана выпуска также используем последнюю таблицу симплекс-метода. Из нее для исследования границ устойчивости цен по виду продукции, которая попала в план производства, составляют систему неравенств, отражающую возможность изменения цены j -го вида продукции на величину D сj исходя из требования сохранения условия неотрицательности переменных двойственной задачи.
Для первого вида продукции, которая попала в план производства, составим систему неравенств:
Þ 
Þ 
.
Учитывая цену первого вида продукции с1 = 4, интервал устойчивости изменения цен составит 
или 
.
Для второго вида продукции, также попавшего в план производства, система неравенств примет вид:
Þ 
Þ 
.
Учитывая цену второго вида продукции с2 = 3, интервал устойчивости изменения цен составит 
или 
.
Для видов продукции, не попавших в оптимальный план производства, исследование допустимых границ изменения цен не проводится.
6. В соответствии с третьей теоремой двойственности представляет частную производную от оптимального дохода по i -му ресурсу. Следовательно, характеризует скорость изменения оптимального дохода при изменении i -го ресурса, а численные значения объективно обусловленных оценок ресурсов показывают, на сколько денежных единиц изменится максимальная прибыль от реализации продукции при изменении запаса соответствующего материального ресурса на одну единицу:
. (7.17)
При увеличении (уменьшении) запаса ресурсов b1 или b2 на единицу максимальная прибыль увеличивается (уменьшается) соответственно на 1 тыс. руб. и 2 тыс. руб., а при изменении запаса ресурса b3 – не изменится.
Также можно установить, насколько изменится максимальная прибыль при изменении ресурсов:
. (7.18)
Следовательно, при изменении запасов сырья на 2 т, ограничение запаса первого вида ресурса увеличится до 6 (6= 4 + 2), что находится в пределах устойчивости оценок ресурсов, а максимальная прибыль изменится на 
тыс. руб.; при изменении количества оборудования на 1 ед., ограничение ресурса второго вида увеличится до 4 (4 = 3 + 1), что также находится в пределах устойчивости оценок ресурсов, максимальная прибыль увеличится на 
тыс. руб. Изменение объемов электроэнергии не приведет к изменению максимальной прибыли. Суммарное влияние всех факторов на прибыль составит 4 тыс. руб. Если изменение запаса ресурса не попадает в интервал устойчивости объективно обусловленной оценки ресурса, то следует изменить условия прямой задачи и решить ее.
7. По соотношению объективно обусловленных оценок могут быть определены расчетные нормы взаимозаменяемости ресурсов, при соблюдении которых проводимые замены в пределах устойчивости двойственных оценок не влияют на эффективность оптимального плана.
Исследование взаимозаменяемости ресурсов производится с помощью коэффициента взаимозаменяемости 
, который показывает, сколько единиц ресурса вида i необходимо для того, чтобы компенсировать уменьшение ресурса k на единицу
. (7.19)
Для взаимозаменяемых ресурсов (коэффициент взаимозаменяемости >0, но отличен от бесконечности) количество ресурса ∆ bi вида i, необходимое для замены выбывающего количества ∆ bk ресурса k, определяется по формуле:
. (7.20)
Составим таблицу взаимозаменяемости ресурсов по условию рассматриваемой задачи из п. 5.3:
|
|
|
|
|
| |||
|
| 1/2 | ||
|
| ¥ | ¥ | - |
Поскольку ресурсы первого и второго вида взаимозаменяемые, то чтобы компенсировать убыток, получаемый при исключении из производства ∆ b2 = 2 ед. второго ресурса, и сохранить максимальный доход на прежнем уровне, в производство следует ввести
единицы.
Этот вывод действителен в пределах устойчивости двойственных оценок, когда изменение запасов ресурсов D b1, D b2, D b3 удовлетворяют границам соответствующего допустимого интервала изменения ресурсов.
8. Для оценки целесообразности приобретения дополнительного количества ресурса ∆ bi вида i по цене сk необходимо сравнить предлагаемую цену с рассчитанной ранее теневой ценой этого ресурса . Приобретение дополнительного количества ресурса целесообразно, если выполняется условие непревышения новой цены над теневой ценой
сk £ . (7.21)
В противном случае приобретение дополнительного количества ресурса нецелесообразно.
Данное условие проверяется, если величина дополнительного ресурса не выходит за границы соответствующего допустимого интервала изменения ресурсов. Если это требование не выполняется, то для ответа на вопрос следует изменить условия прямой задачи и решить ее.
Таким образом, чтобы оценить целесообразность приобретения ∆ b2 = 1 единицы второго ресурса по цене сk = 2 тыс. руб. за единицу, проверим, находится ли данное изменение в границах допустимого интервала изменения ресурсов: . Поскольку 3 + 1 =4 находится в установленных границах, то можем оценить целесообразность приобретении одной единицы оборудования. Так как 2 = 2, то условие (7.21) выполнено, и приобретение дополнительной единицы оборудования целесообразно.
