Каждой задаче линейного программирования можно поставить в соответствие так называемую двойственную или сопряженную задачу по отношению к исходной задаче. Аппарат теории двойственности может быть эффективно использован для проведения качественных исследований свойств задачи линейного программирования.
Рассмотрим задачу выбора оптимальной производственной программы. Пусть предприятие № 1 имеет запасы материально-сырьевых ресурсов в объемах bi (
), где m – число видов ресурсов. Как и раньше будем считать, что aij – это объем материально-сырьевых ресурсов вида i, необходимых для производства одной единицы продукции вида j, cj – прибыль от выпуска и реализации единицы продукции вида j (
).
Далее будем считать, что предприятие № 2 решило купить все материально-сырьевые ресурсы у предприятия № 1 по некоторым оптимальным ценам на эти ресурсы, которые обозначим как y1, ¼, ym. Естественно, что предприятие № 2 заинтересовано в том, чтобы затраты на приобретение материально-сырьевых ресурсов были минимальными, т.е.
.
С другой стороны, предприятие № 1, которое продает материально-сырьевые ресурсы, заинтересовано в том, чтобы полученная выручка была не менее той суммы, которую предприятие может получить при использовании ресурсов на производство готовой продукции.
Для изготовления единицы продукции вида 1 расходуется a11 ресурсов первого вида, a21 ресурсов второго вида, ¼, ai1 ресурсов i -го вида. Поэтому для того чтобы удовлетворить требованиям продавца (предприятие № 1), затраты на ресурсы, используемые для изготовления одной единицы продукции первого вида, должны быть не менее ее цены с1. Иными словами, необходимо выполнение неравенства следующего вида:
.
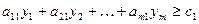Аналогично можно представить ограничения по всем остальным видам продукции 2, 3, ¼, n. Экономико-математическая модель и содержательная интерпретация получаемой таким образом задачи представлена в правой части табл. 7.1.
Таблица 7.1
| Исходная (прямая) задача (I) | Двойственная задача (II) |
 (7.1)
при ограничениях:
 (7.2)
и условие неотрицательности  (7.3)
составить такой план выпуска продукции  , при котором прибыль (выручка) от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов
| (7.4)
при ограничениях:
 (7.5)
и условие неотрицательности  (7.6)
найти такой набор цен ресурсов  , при котором общие затраты на ресурсы будут минимальными при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли (выручки) от реализации продукции
|
Цены ресурсов y1, ¼, ym в экономической литературе получили различные названия: учетные, неявные, теневые. Смысл их названий состоит в том, что в отличие от цен на полученную продукцию, которые достаточно точно могут прогнозироваться, цены ресурсов y1, ¼, ym являются внутренними, так как они задаются не извне, а определяются в результате решения задачи, поэтому их часто называют оценками ресурсов.
Исходная и двойственная задачи обладают следующими характеристиками.
1. В первой задаче определяется максимум линейной целевой функции, во второй – минимум.
2. Коэффициенты при переменных в целевой функции первой задачи являются правыми частями в системе ограничений во второй задаче.
3. Каждая из задач задана в стандартной форме, при этом в задаче максимизации все неравенства вида «меньше или равно», а в задаче минимизации все неравенства вида «больше или равно».
4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу.
Для задачи I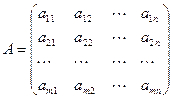 
.
Для задачи II 
.
5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
6. Условие неотрицательности переменных имеются в обеих задачах.
Задачи (I и II) линейного программирования, обладающие указанными характеристиками, называются симметричными взаимодвойственными задачами. Далее будем называть их двойственными задачами. Задачу (I) еще называют исходной или прямой паре двойственных задач. Исходя из описанных характеристик двойственных задач можно сформулировать следующее правило формирования двойственной задачи.
1. Привести все неравенства системы к одному виду: если в исходной задаче ищется максимум целевой функции, то все неравенства системы ограничений приводятся к виду «меньше или равно», а если минимум – к виду «больше или равно». Для этого неравенства, не удовлетворяющие требованиям, умножают на (-1).
2. Составить расширенную матрицу А1, в которую включить матрицу коэффициентов при переменных А, столбец правых частей исходной системы ограничений и строку коэффициентов при переменных в целевой функции.
3. Сформировать матрицу А1¢, транспонированную к матрице А1.
4. Сформировать двойственную задачу на основании полученной матрицы А1¢ и условия неотрицательности переменных.
Пример формирования двойственной задачи. Пусть исходная или прямая задача линейного программирования (ПЗЛП) состоит в определении максимума целевой функции
при ограничениях:
.
Решение.
1. Так как исходная задача на максимум, то обе части первого и четвертого неравенства умножим на (-1). Получим:
.
2. Составим расширенную матрицу системы:
.
3. Найдем матрицу А1¢, транспонированную к матрице А1:
.
4. Сформулируем двойственную задачу
при ограничениях:
.
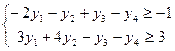
