Найденное опорное решение проверяется на оптимальность методом потенциалов по следующему критерию: если опорное решение транспортной задачи является оптимальным, то ему соответствует система m + n действительных чисел ui и vj, удовлетворяющих условиям ui + vj = cij для занятых клеток и ui + vj – cij £ 0 для свободных клеток.
Числа ui и vj называют потенциалами. В распределительную таблицу добавляют строку vj и столбец ui.
Потенциалы ui и vj находят из равенства ui + vj = cij, справедливого для занятых клеток. Одному из потенциалов дается произвольное значение, например, u1 = 0, тогда остальные потенциалы определяются однозначно. Так, если известен потенциал ui, то vj = cij - ui, если известен потенциал vj, то ui, = cij - vj.
Обозначим D ij = ui + vj - cij, которую называют оценкой свободных клеток. Если все оценки свободных клеток D ij £ 0, то опорное решение является оптимальным. Если хотя бы одна из оценок D ij ≥ 0, то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.
Проверим найденное опорное решение на оптимальность, добавив в распределительную таблицу столбец ui и строку vj.
| bj ai | ui | ||||
| - | - | ||||
| - | –2 | ||||
| - | |||||
| vj |
Полагаем u1 = 0, запишем это значение в последнем столбце первой строки таблицы.
Рассмотрим занятую клетку первой строки, которая расположена в первом столбце (1, 1), для нее выполняется условие u1 + v1 = 2. Откуда при u1 = 0, v1 = 2, это значение запишем в последней строке таблицы. Далее рассматривают ту из занятых клеток таблицы, для которых один из потенциалов известен.
Рассмотрим занятую клетку (3, 1): u3 + v1 = 3, v1 = 2, откуда u3 =1.
Для клетки (3, 3): u3 + v3 = 8, u3 = 1, v3 =7.
Для клетки (2, 3): u2 + v3 = 5, v3 = 7, u2 = –2.
Для клетки (2, 2): u2 + v2 = 1, u2 = –2, v2 = 3.
Найденные значения потенциалов заносим в таблицу.
Вычисляем оценки свободных клеток:
D 12 = u1 + v2 - c12 = 0 + 3 – 5 = –2 < 0,
D 13 = u1 + v3 - c13 = 0 + 7 – 2 = 5 > 0,
D 21 = u2 + v1 - c21 = -2 + 2 – 4 = – 4 < 0,
D 32 = u3 + v2 - c32 = 1 + 3 – 6 = –2 < 0.
Получили одну оценку D 13 = 5 > 0, следовательно, исходное опорное решение не является оптимальным и его можно улучшить.
Наличие положительной оценки свободной клетки (D ij ≥ 0) при проверке опорного решения на оптимальность свидетельствует о том, что полученное решение не оптимально, и для уменьшения значения целевой функции надо перейти к другому опорному решению. При этом надо перераспределять грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых – свободной.
Для свободной клетки, у которой D ij ≥ 0, строится цикл (цепь, многоугольник), все вершины которого, кроме одной, находятся в занятых клетках, углы прямые, число вершин четное. Около свободной клетки цикла ставится знак (+), затем поочередно проставляют знаки (–) и (+). У вершин со знаком (–) выбирают минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают от грузов у вершин со знаком (–). В результате перераспределения груза получим новое опорное решение. Это решение проверяем на оптимальность, и т.д. до тех пор, пока не получим оптимальное решение.
Рассмотрим переход от одного опорного решения к другому на заданном примере.
Строим цикл для клетки (1, 3), имеющей положительную оценку D 13 = 5 > 0. У вершин цикла ставим знаки (+) и (–) и записываем грузы.
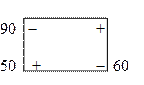
У вершин со знаком (-) выбираем минимальный груз, он равен 60. Его прибавляем к грузам, стоящим у положительных вершин, и отнимаем от грузов, стоящих у отрицательных вершин. Получаем новый цикл:

Новое опорное решение:
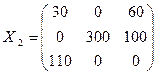 .
.
Проверим полученное решение на оптимальность. Для этого запишем полученное решение в распределительную таблицу, найдем потенциалы занятых и оценки свободных клеток.
| bj ai | ui | ||||
| - | |||||
| - | |||||
| - | - | ||||
| vj | -2 |
D 12 = – 7, D 21 = 1 > 0, D 32 = – 7, D 33 = – 5.
Построим цикл для клетки с положительной оценкой D 12 = 1:
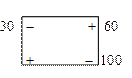
Произведем перераспределение грузов:

Получаем новое решение, которое заносим в таблицу. Проверим его на оптимальность.
| bj ai | ui | ||||
| - | - | ||||
| - | - | ||||
| vj | -2 |
D 11 = – 1, D 12 = – 7, D 32 = – 6, D 33 = – 4.
Все оценки свободных клеток отрицательные, следовательно, найденное решение оптимальное.
Ответ: 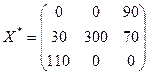 .
.
Стоимость транспортных расходов:
L(X)min = 90×2 + 30×4 + 300×1 + 70×5 + 110×3 = 1280 ден. ед.
По сравнению с исходным опорным решением транспортные расходы уменьшились на 1610 – 1280 = 330 ден. ед.
Замечание. Если при проверке оптимальности решения положительные оценки имеют несколько клеток, то цикл перераспределения поставок строят, начиная с клетки (i, j) с максимальным значением оценки:
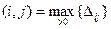 .
.
Форма цикла может быть разной, например:

Но для клетки с положительной оценкой он является единственным.






