16. По круговоаму витку радиуса R циркулирует ток I. Определить индукцию магнитного поля на оси витка в зависимости от расстояния х от его центра. Построить график этой зависимости. Исследовать предельные случаи x<<R и x>>R.
Решение
 |
Вследствие осевой симметрии полный вектор индукции на оси Ох направлен вдоль этой оси.
По закону Био-Савара вклад в проекцию вектора индукции магнитного поля на ось Ох от элемента длины кольца dl, расположенного в точке А (на рисунке) составляет dBх=(m0/4p)(Idl/r2)sina. Вектор 
лежит в плоскости, проходящей через ось Ох и точку А и перпендикулярен 
. Величина sina=R/r одна и та же для всех точек кольца. Полная величина магнитной индукции составляет
B(x)=(m0/2)IR2/r3=(m0/2)IR2/(R2+x2)3/2
При x<<R B(x)=m0I/2R, при x>>R B(x)=(m0/2)IR2/x3.
17. Длинный проводник с током I = 3А изогнут в форме прямого угла. Определить индукцию магнитного поля в точке, лежащей на биссектрисе угла на расстоянии L = 10 см от вершины угла О.
Решение
Сначала найдем индукцию магнитного поля, создаваемого прямолинейным отрезком длиной D проводника с током I. Пусть R – длина перпендикуляра, проведенного на отрезок из точки наблюдения, r – расстояние от точки наблюдения до элемента отрезка длиной dl, da=dl/r –угол, под которым виден элемент отрезка dl из точки наблюдения. Пусть также a - угол между перпендикуляком к отрезку и прямой, проведенной из точки наблюдения к элементу отрезка, тогда R=rcosa. По закону Био-Савара вклад в индукцию магнитного поля элемента отрезка dl составит
dB=(m0/4p)(Idl/r2)= (m0/4p)(Icosa da/R).
После интегрирования по длине отрезка получается
B=(m0/4p)(I/R)(sina1 - sina2).
Здесь a1 и a2 - углы между перпендикуляком к отрезку и прямыми, проведенными из точки наблюдения к концам отрезка.
Индукция магнитного поля в точке, лежащей на биссектрисе угла на расстоянии L от вершины угла, создается двумя лучами, являющимися сторонами угла. Вследствие симметрии относительно биссектрисы угла вклад в индукцию каждого из лучей одинаков.
Для одного луча a1=p/2, a2=-p/4, R=Lcos(p/4), и
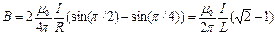= 2 10-6(3/0.1)0.42=2.48 10-5 Тл
18. По длинному прямому цилиндрическому проводу радиуса R течет ток с постоянной плотностью j. Определить индукцию магнитного поля как функцию расстояния r от оси провода и построить график этой зависимости.
Решение
Индукция магнитного поля обладает в этой задаче осевой симметрией и вследствие однородности вдоль проводника от координаты вдоль проводника не зависит. Силовые линии поля – концентрические окружности с общим центром на оси проводника. Вектор индукции направлен по касательным к этим окружностям. Эти окружности следует выбрать в качестве замкнутых контуров для применения теоремы о циркуляции:
где I=pR2j – полный ток в проводнике. Отсюда следует
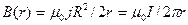r<R
r>R
19. По оси длинного тонкостенного проводящего цилиндра радиуса R натянут провод. По цилиндру и проводу течет постоянный ток силы I, направление тока в проводе и цилиндре противоположны. Определить индукцию магнитного поля в зависимости от расстояния r от провода и построить график этой зависимости.
Решение
Индукция магнитного поля обладает в этой задаче осевой симметрией и вследствие однородности вдоль проводника от координаты вдоль проводника не зависит. Силовые линии поля – концентрические окружности с общим центром на оси проводника. Вектор индукции направлен по касательным к этим окружностям. Эти окружности следует выбрать в качестве замкнутых контуров для применения теоремы о циркуляции:
0<r<R
0<r<R
, B(r)=0 r>R,
20. Тороидальная однослойная катушка содержит N витков плотно намотанного провода, по которому течет ток I. Внутренний радиус тора R1,внешний - R2. Определить индукцию магнитного поля внутри и вне тора на расстоянии r от его оси.
Решение
Тор представляет собой поверхнсть вращения окружности радиуса R = (R2 - R1)/2 вокруг оси, расположенной вне окружности. Полагая провод тонким по сравнению с радиусом тора, можно считать, что линии тока лежат в меридианальных плоскостях, т.е. в плоскостях, проходящих через ось вращения. При этом предположении при повороте тора с намотанным на него проводом с током вокруг оси он совмещается сам с собою. То же относится и к силовым линиям индукции магнитного поля тока. Поэтому силовые линии поля представляют собой концентрические окружности с центрами на оси вращения. Циркуляция вектора индукции магнитного поля вдоль каждой такой окружности радиуса r равна 2prB(r) Полный ток, пронизывающий площадь, ограниченную этой окружностью, равен NI, если окружностьпроходит внутри тора, и равен нулю, если она проходит вне тора.Таким образом, индукция поля отлична от нуля только внутри тора, т.е при R1 <r< R2 и составляет 
. Величина n=NI/2pr представляет собой число витков, приходящееся на единицу длины обмотки. Величина i=nI представляет собой линейную плотность тока.
21. Соленоид представляет собой полый цилиндр радиуса R и длины L, на поверхность которого плотно намотан в один слой тонкий провод. Отношение числа витков провода в обмотке соленоида к его длине составляет n. Определить индукцию магнитного поля внутри и вне соленоида, если по его обмотке течет ток I. Провести оценки для следующих величин: R=1 см, L=50 см, n=15 витков/см, I=1 А.
Решение
Соленоид можно представить себе как предельный случай тора очень большого радиуса вращения, но фиксированного радиуса цилиндра R при увеличении числа витков обмотки, но фиксированном отношении n числа витков к длине окружности вращения. Индукция магнитного поля внутри соленоида составляет B= m0nI, вне соленоида B =0.
Давление магнитного поля p=B2/2m0. Сила давления, действующая на боковую поверхность соленоида, площадь которой S=2pRL составит
F=pS=m0(nI)2S/2=pm0(nI)2RL
Численные оценки:
B=1.256 10-6 15 1=1.88 10-5 Тл p=1.41 10-4Н/м2 F=4.44 10-6 Н
