Задача Д1.
В масс-спектрометре заряженные частицы массой m и зарядом q первоначально ускоряются в электрическом поле, проходя без начальной скорости разность потенциалов U. Затем они поступают в магнитное поле с индукцией B перпендикулярно направлению поля и движутся в магнитном поле по окружности радиуса R. Определить удельный заряд частиц q/m.
Решение.
При ускорении заряженной частицы в электрическом поле потенциальная энергия частицы, при прохождении разности потенциалов U составляющая qU, переходит в кинетическую энергию:
При попадании частицы в магнитное поле перпендикулярно направлению поля частица под действием силы Лоренца движется по дуге окружности радиуса R:
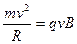
Отсюда получается vBR=2U, или v=2U/RB. С другой стороны, из второго уравнения следует v=(q/m)RB, и окончательно
(q/m)=2U/(RB)2.
Задача Д2.
Плоская прямоугольная катушка из N =100 витков со сторонами a=10 см и b=20 см находится в однородном магнитном поле с индукцией В= 0.1 Тл. Каков максимальный вращающий момент может действовать на катушку, если сила тока в катушке I =2A.
Решение.
Пусть ось x направлена вдоль одной из сторон катушки, ось y – вдоль другой стороны, ось z - параллельно нормали к плоскости катушки, начало координат выбрано в одной из вершин катушки. При вращении правого винта по направлению тока в катушке винт движется в
направлении единичного вектора нормали 
. На рисунке показаны положение и размеры
катушки и направление тока I. В выбранной системе координат вектор нормали совпадает с базовым вектором 
системы координат. Токи в проводниках 03 и 12 противоположны по направлению, а длины этих проводников равны. Поэтому силы Ампера, действующие на эти проводники, равны и противоположны, т.е. образуют пары сил. Момент пары этих сил составляет 
. Аналогично, момент пары сил, действующих на проводники 01 и 23 составляет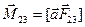 
. Для сил Ампера имеем 
, 
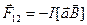. Подставляя выражения для сил Ампера в выражения для моментов и раскрывая по правилам двойные векторные произведения, для полного момента сил, действующих на виток катушки, получается следующее выражение
Замечая, что векторное произведение 
, полный момент сил Ампера, действущих на виток катушки, можно представить в виде
,
где S=ab – площадь витка. Можно определить магнитный момент витка с током как 
, вектор нормали к плоскости витка образует правовинтовую систему с направлением тока в витке. Тогда момент сил Ампера составит 
. Последние два выражения записаны в инвариантой виде, т.е. не зависят от выбора системы координат и применимы для витков любой формы.
Складывая моменты сил, действующих на каждый виток катушки, получаем полный момент сил
,
Он максимален, когда вектор индукции перпендикулярен нормали к плоскости витков катушки и составляет Mмакс=NISB. Подставляя численные значения, находим
Mмакс=100 2 0.1 0.2 0.1=0.4 Н м
