Глава 7. Интегральное исчисление
Первообразная функция и неопределенный интеграл
Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Интегральное исчисление решает обратную задачу – нахождение самой функции по ее производной или дифференциалу.
Определение
Функция называется первообразной для функции 
на промежутке X, если в каждой точке этого промежутка функция 
дифференцируема и выполняется равенство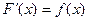 
.
Рассмотрим несколько примеров.
1. Функция 
является первообразной для функции 
на бесконечном промежутке 
, так как при любых x выполняется равенство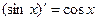 
.
2. Функция 
есть первообразная для функции 
на промежутке 
.
3. Функция 
– первообразная для 
на промежутке .
Заметим, что задача отыскания по заданной функции ее первообразной неоднозначна; если первообразная, то и функция 
, где C – произвольное постоянное число, также является первообразной функции , так как 
.
Возникает вопрос, описывает ли выражение все первообразные для функции ? Ответ на него дает следующая Теорема.
Теорема
Если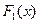 
и 
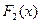– первообразные для функции в некотором промежутке X, то найдется такое число C, что справедливо равенство
| (7.1.1) |
иными словами, все первообразные для функции отличаются друг от друга на константу.
Из теоремы вытекает, что множество функций , где – одна из первообразных для функции , а C – произвольная постоянная, образует семейство первообразных для функции .
Определение
Совокупность всех первообразных функций для функции на промежутке X называется неопределенным интегралом от функции на этом промежутке и обозначается символом
 .
| (7.1.2) |
В этой записи знак 
называется знаком интеграла (это стилизованная латинская буква S, означающая суммирование), – подынтегральной функцией, 
– подынтегральным выражением, а переменная x – переменной интегрирования. Операция нахождения первообразной по ее производной или неопределенного интеграла по заданной подынтегральной функции называется интегрированием этой функции. Интегрирование является операцией, обратной дифференцированию. Для проверки правильности выполнения интегрирования нужно продифференцировать результат и получить при этом подынтегральную функцию.
Пример
; проверка: 
; проверка: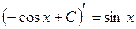 
.
Свойства неопределенных интегралов
Прежде всего отметим свойства, которые непосредственно вытекают из определения неопределенного интеграла:
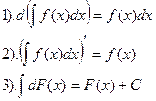
| (7.2.1) |
Для доказательства свойства 1 достаточно взять дифференциал от обеих частей выражения (7.2.1) и записать, что 
. Для установления свойства 2 нужно в левой части выражения (7.2.1) использовать запись дифференциала и Определение первообразной: 
.
Следующие два свойства называются линейными свойствами неопределенного интеграла:
, где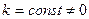 
.
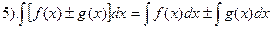Свойство 4 вытекает из свойства для производной функции : 
. Свойство 5 есть следствие того, что если и 
– первообразные функций и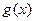 
, то производная их суммы равна сумме их производных.
Заметим, что последнее свойство справедливо для любого конечного числа слагаемых в подынтегральной функции.
