Задание 1.
Решение задачи типа 1-10.
Решить систему уравнений следующими методами:
а) методом Крамера,
б) матричным методом.
Решение:
а) Составим определитель системы:
Для его вычисления воспользуемся свойством определителя о том, что величина определителя не изменится, если к элементам любой его строки (столбца) прибавить элементы любой другой строки (столбца), умноженной(го) на число.
(Первую строку умножаем на (-1) и прибавляем ко второй и к третьей строке).
Получим: 
Применяя свойство о разложении определителя по элементам любой строки (столбца) (в данном случае по элементам первого столбца), получим:
Составим вспомогательные определители и вычислим их аналогичным образом:
вычисляются по формулам:
б) Для решения системы матричным методом введем обозначения матриц:
(1)
Т.к.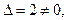 
то для матрицы А существует обратная матрица А-1. Найдем обратную матрицу. Для этого вычислим алгебраические дополнения всех элементов главного определителя 
системы
Союзной матрицей А* для матрицы А будет матрица:
то 
Учитывая равенство (1), имеем:
Задание 2.
Решение задачи типа 11-20.
Выясните, образуют ли вектора 
, 
, 
базис. Если образуют, то разложить вектор 
по этому базису.
Решение:
Вычисляем 
Следовательно, векторы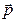 
, 
, 
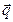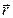образуют базис, и вектор 
линейно выражается через базисные векторы: 
или в координатной форме
Решаем полученную систему по формулам Крамера.
Находим: 
поэтому
Задание 3.
Решение задачи типа 21-30.
Даны координаты вершин пирамиды 
:
Найти:
1. Длину ребра 
, если
Решение:
Ответ: 
2. Угол между ребрами и 
, если
Решение:
Найдем координаты векторов по формулам: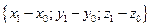 
Угол между векторами и вычисляется по формуле: 
Ответ: 
3. Угол между ребром и гранью 
.
Решение:
Найдем уравнение плоскости, содержащей точки 
.
- уравнение плоскости.
Вектор нормали к этой плоскости имеет координаты 
Косинус угла между плоскостью и вектором равен синусу угла между этим вектором и вектором нормали.
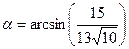
Ответ: 
4. Площадь грани
Решение:
Грань 
- треугольник, его площадь вычислим по формуле
, где 
- модуль векторного произведения двух векторов (сторон треугольника), по определению он равен произведению длин двух векторов на синус угла между ними, т.е. 
.
Найдем векторное произведение векторов 
и 
Результатом будет вектор с координатами 
, найдем его длину
Ответ: 
5. Объем пирамиды.
Решение:
, где - 
- смешанное произведение векторов , и
Ответ: 
6. Уравнение прямой 
Решение:
Каноническое уравнение прямой имеет вид:
, где 
- точка, принадлежащая прямой - 
, 
- направляющий вектор этой прямой – .
Ответ: 
7. Уравнение плоскости 
.
См. пункт 3)
- уравнение плоскости.
Ответ:
Уравнение высоты, опущенной из вершины 
на грань .
Вектор нормали к этой плоскости имеет координаты , т.е. он и будет направляющим вектором высоты
Ответ: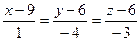 
Задание 4.
Решение задачи типа 31-40
Даны две вершины 
и 
и точка 
пересечения медиан треугольника ABC. Составить уравнение высоты треугольника, проведенной через третью вершину С.
Решение:
а) Найдем точку пересечения стороны АВ с медианой проведенной к ней.
б) Найдем координаты точки С из того факта, что медианы точкой пересечения делятся в отношении 2:1, считая от вершины.
Обозначим координаты (x,y).
в) Найдем координаты вектора 
и
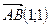
Направляющим вектором высоты, проведенной к стороне АВ будет вектор, перпендикулярный найденному, т.е., например
(-1;1).
С(-2;3)
Эта прямая совпадает с прямой, содержащей медиану АМ.
Ответ: y = -x+1.
Задание 5.
Решение задачи типа 41-50
Привести уравнение кривой второго порядка 
к каноническому виду и построить кривую.
Решение:
Для приведения уравнения кривой второго порядка к каноническому виду применяют метод выделения полного квадрата.
Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при 
и 
вынесем за скобки: 
.
Выделим полный квадрат: 
.
Отсюда 
. Разделим обе части равенства на 25: 
. Запишем полученное уравнение в каноническом виде: 
.
Выполним параллельный перенос осей координат по формулам 
. При таком преобразовании начало координат переносится в точку 
, уравнение эллипса принимает канонический вид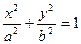 
.
В нашем примере 
, 
, 
, 
.
Итак, рассматриваемое уравнение определяет эллипс с центром в точке 
и полуосями 
и 
.
Задание 6.
Решение задачи типа 51-60.
Линия задана уравнением 
в полярной системе координат. Требуется построить линию по точкам, начиная от 
до 
и придавая 
значения через промежуток 
.
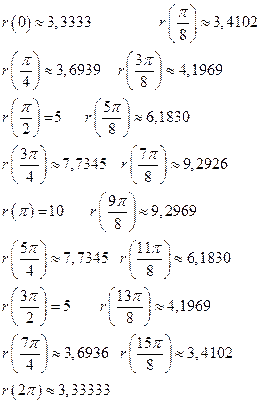
Задание 7.
Дано комплексное число 
. Записать это число в алгебраической и тригонометрической формах.
Решение:
Чтобы записать число z в алгебраической форме 
, умножим числитель и знаменатель на число, сопряженное знаменателю
Итак, алгебраическая форма числа 
.
Запишем данное число в тригонометрической форме. Имеем: 
. Получим:
; 
; 
.
Угол, для которого косинус положителен, а синус отрицателен, находится в четвертой четверти. Следовательно, 
. Число z в тригонометрической форме запишется в виде: 
Задание 8.
Решение задачи типа 71-80
Найти пределы функций, не пользуясь правилом Лопиталя.
а) 
| б)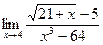 
|
в) 
| г)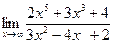 
|
д) 
| е)
|
ж) 
|
Решение:
а)
Имеем неопределенность вида 
. Для ее раскрытия разложим квадратные трехчлены на линейные множители по формуле 
Имеем:
Сократив общий множитель 
, получим:
б)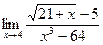
Имеем неопределенность вида . Для ее раскрытия умножим, и числитель, и знаменатель данной дроби на выражение, сопряженное числителю (знаменателю), а именно: 
. Имеем:
Для упрощения числителя воспользуемся формулой:
 , где  , 
|
Разложим первый сомножитель знаменателя по формуле:
 , где 
|
в)
Если числитель и знаменатель дроби представляют собой алгебраические многочлены и имеется неопределенность вида 
, то для ее раскрытия и числитель, и знаменатель делят на х в старшей степени. В данном случае старшая степень 3, поэтому, и числитель, и знаменатель делим на 
, имеем:
(по теореме о пределе частного, имеем)
(по теореме о пределе суммы, имеем)
г)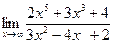
Имеем также неопределенность вида .
Старшая степень х равна 5. Поэтому делим и числитель, и знаменатель на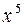 
. Имеем:
т.к. предел числителя равен 2, а знаменателя 0.
д)
Для вычисления данного предела, и числитель, и знаменатель дроби делим на , имеем:
е)
Имеем неопределенность вида: 
.
Для ее раскрытия воспользуемся вторым замечательным пределом:
или 
ж)
Имеем неопределенность вида . Для ее раскрытия будем использовать первый замечательный предел: 
Для этого сделаем следующие преобразования:
Задание 9.
Решение задачи типа 81-90
Исследовать на непрерывность, выяснить характер точек разрыва и изобразить графически следующие функции
Решение:
а) Построим график данной функции, составляющими которой являются линейная функция 
, квадратичная функция 
(на промежутке 
) и линейная функция 
.
 |
х
Исследуем функцию на непрерывность. К точкам, в которых возможно функция терпит разрыв, относятся точки 
(точки, где функция меняет свое аналитическое задание).
Для того, чтобы функция в точке 
была непрерывна необходимо и достаточно, чтобы
Проверим это условие для точки 
:
Условие выполнено, значит функция в точке 
непрерывна.
Аналогичным образом исследуем на непрерывность в точке 
.
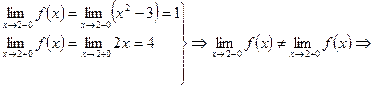
Функция в точке 
терпит разрыв I рода.
Задание 10.
Решение задачи типа 91-100
Найти производные следующих функций:
а) 
б) 
| в) 
г) 
|
Решение:
а)
При нахождении производной данной функции воспользуемся следующими формулами: 
Имеем:
б)
При вычислении производной данной функции воспользуемся формулой: 
Имеем:
(*)
При вычислении производной первого сомножителя воспользуемся формулой , где
При вычислении производной второго сомножителя воспользуемся следующей формулой: 
Подставляя вычисленные производные в равенство (*), имеем:
в)
В данном случае сначала воспользуемся формулой:
Производную числителя и знаменателя вычисляем, используя формулу
,
т.к. 
.
.
В результате:
.
Задание 11.
Решение задачи типа 101-110.
Найти 
для функции, заданной параметрически:
Решение:
По формуле 
Имеем:
.
Для нахождения производной второго порядка воспользуемся формулой 
Задание 12.
Исследовать методами дифференциального исчисления функцию. На основании результатов исследования построить график этой функции 
Решение:
1) 
.
2) Функция ни четная, ни нечетная.
3) асимптоты
а) 
,
-вертикальная асимптота.
б) 
.
Следовательно, 
- наклонная асимптота.
4) 
при 
не существует при 
-точка максимума функции.
-точка минимума функции.
5) 
не существует при
6) Найдем точки пересечения с осями:
При 
.
При 
квадратное уравнение не имеет корней, следовательно график не пересекается с осью 
Задание13.
Найти частные производные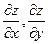 
функции 
Решение:
Считая постоянной (тогда и 
const), находим:
Считая 
постоянной, имеем:
Задание 14.
Найти неопределенные интегралы.
а) 
.
Решение:
Т.к. 
, то
Проверка:
Решение:
Положим 
Найдем 
Применяя формулу интегрирования по частям 
Решение:
Данная подынтегральная дробь – неправильная, поэтому сначала выделим целую часть 
Представим дробь 
в виде суммы простейших дробей:
Тогда 
, следовательно 
.
Получим
Решение:
Применим формулу понижения степени:
Задание 15.
Вычислить площадь фигуры, ограниченной линиями: 
Решение:
Найдем абсциссы точек пересечения прямой с параболой, решив систему уравнений:
Решая эту систему получим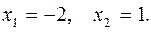 
Это и будут пределы интегрирования. Это и будут пределы интегрирования.
Итак, данные линии пересекаются в точках A (-2; 0), B (4; 6).
Эти линии образуют замкнутую фигуру, площадь которой равна:
Задание 16.
Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболой 
и осью Oх.
Решение:
Графиком функции является парабола с вершиной в точке (1;1), пересекающая ось Oх в точках (0;0) и (2;0). Таким образом, отрезок интегрирования – [0;2].
Объем тела, образованного вращением вокруг оси Oх, фигуры ограниченной линиями 
и прямыми 
вычисляется по формуле: 
.
Получим: 
Задание 17.
Вычислить несобственный интеграл 
или доказать его расходимость.
Решение:
В силу определения имеем:
Интеграл сходится.
Задание 18.
Найти общее решение дифференциального уравнения первого порядка.
Решение:
Это уравнение является уравнением с разделяющимися переменными т.к. коэффициент при dx представляет собой произведение двух сомножителей: ex зависит только от x, а (1 +y2) – только от y. Аналогично, коэффициент при dy тоже является произведением двух сомножителей: (1 +ex) зависит только от x, а второй сомножитель – y.
Чтобы привести его к виду с разделенными переменными, разделим все члены уравнения на (1 +ex)(1 +y2), в результате получим: 
Решим это уравнение. (Заметим, что постоянную С можно записывать как 
).Здесь произвольную постоянную удобнее взять в виде 
.
-это общий интеграл исходного уравнения.
Решение:
Введем замену 
. Тогда 
а 
Заданное уравнение принимает вид:
Возвращаясь, к замене получим:
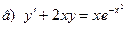
Решение:
Заданное уравнение является ЛНДУ. Будем искать решение уравнения в виде произведения двух функций: 
. После этой подстановки данное уравнение примет вид: 
Вынесем за скобки u:
(*)
Найдем одну из функций v, такую, чтобы выражение в скобках обратилось в нуль: 
. Это уравнение будет с разделяющимися переменными. Решим его.
Подставим найденную функцию в уравнение (*).
Т.к. y = uv, то 
- общее решение данного уравнения.
Задание 19.
Найти общее решение дифференциального уравнения второго порядка, допускающего понижение порядка:
Общее решение этого уравнения находим последовательным трехкратным интегрированием. Имеем:
,
,
.
Полагаем 
, тогда 
и уравнение примет вид:
.
Интегрируя получим: 
, 
.
Следовательно, 
.
Интегрируя последовательно три раза, получим:
.
Полагаем 
, тогда
.
Уравнение примет вид: 
.
Решая его получим:
или 
, 
или 
.
Решая уравнение, мы делили его на 
и на 
.
Но 
и 
могут быть включены в общее решение, если считать, что 
и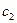 
могут принимать значение ноль.
Задание 20.
Решить задачу Коши:
Решение:
Характеристическое уравнение: 
имеет корни 
Корни характеристического уравнения комплексные сопряженные им соответствуют частные решения 
Следовательно, общее решение 
Подставляя начальные условия в найденное общее решение и его производную:
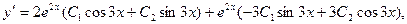
получим систему: 
Решая ее, получим: 
.
Тогда частное решение примет вид: 
Задание 21.
Решить линейное неоднородное дифференциальное уравнение:
Решение:
характеристическое уравнение 
имеет корни 
Поэтому общее решение однородного уравнения будет иметь вид:
Частное решение будем искать в виде:
Найдем коэффициенты А, В и С, для этого и 
подставим в исходное уравнение.
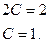
Отсюда 
- частное решение неоднородного уравнения.
Общее решение
Задание 22.
Найти общее решение системы уравнений: 
Решение:
Составим характеристическое уравнение системы
или 
При 
уравнения для определения собственного вектора имеют вид:
и сводятся к одному уравнению: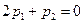 
.
Из которого определяем вектор, например, 
. При 
получаем уравнения
или 
Это уравнение определяет вектор, например, 
.
Получаем функциональную систему решений:
при 
при 
Общее решение системы имеет вид:
Задание 23.
С помощью двойного интеграла вычислить площадь фигуры D, ограниченной линиями 
Решение:
Эту площадь удобно вычислять, считая у внешней переменной. Тогда границы области задаются уравнениями 
и
где 
вычисляется с помощью интегрирования по частям:
Следовательно, 
Задание 24.
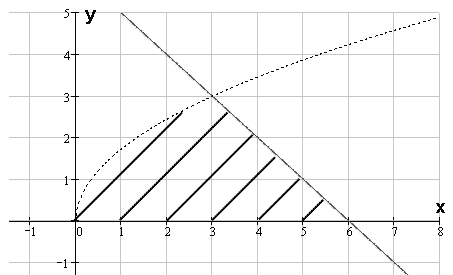
С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями: 
. Сделать чертеж проекции данного тела на плоскость Оху
Решение:
Найдем проекцию тела на плоскость Оху
Задание 25
Вычислить криволинейный интеграл первого рода:
где 
Решение:
Вычисление криволинейного интеграла 1-го рода может быть сведено к вычислению определенного интеграла, причем способ такого сведения зависит от представления кривой интегрирования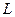 
. Если 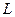задана уравнением 
где функция 
имеет непрерывную производную 
для 
, то
Если 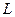задана параметрически: 
где функции 
имеют непрерывные производные 
, для 
то
Если 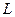задана в полярных координатах уравнением 
и функция 
имеет непрерывную производную 
для 
, то
В рассмотренном примере используется явное задание кривой 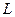уравнением 
. Поэтому, используя первый способ сведения интеграла по длине дуги к определенному, получим:
Задание 26.
Вычислить криволинейный интеграл второго рода
вдоль дуги 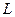дуга параболы 
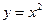от точки 
до точки 
Сделать чертеж.
Решение:
Воспользуемся формулой:
y 
 |
A B
 |
1 2 x
Задание 27
Даны векторное поле 
и плоскость 
которая совместно с координатными плоскостями образует пирамиду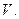 
Пусть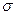 
- основание пирамиды, принадлежащие плоскости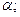 
- контур, ограничивающий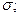 
n- нормаль к 
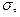направленная вне пирамиды 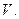Вычислить:
1) поток векторного поля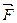 
через поверхности 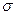внаправлениинормали n;
2) циркуляцию векторного поля 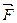по замкнутому контуру непосредственно и применив формулу Стокса к контуру и ограниченной им поверхности 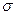с нормалью n;
3) поток векторного поля 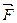через полную поверхность пирамиды 
в направлениивн
