Положение прямой L в пространстве можно однозначно определить, в частности, заданием какой-либо ее фиксированной точки М 0 и ненулевого вектора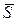 
, коллинеарного этой прямой. Такой вектор называется направляющим вектором прямой.
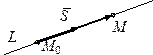Пусть прямая L проходит через точку 
в направлении вектора 
. Так как важно направление, а не точка приложения вектора 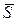, то его всегда можно отложить так, чтобы прямая проходила через него, например, поместив его начало в точку 
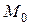. Возьмем на прямой произвольную точку 
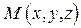и соединим ее вектором с М 0. Тогда вектора 
– коллинеарны, т.к. лежат на одной прямой. Т.к. координаты коллинеарных векторов пропорциональны, то:
.
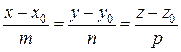Параметрические уравнения прямой
Примем каждое из отношений в предыдущих уравнениях за параметр t, который может принимать любые значения, т.к. m, n, p – заданы, а координаты x, y, z могут принимать любые значения.
,
откуда 
Наиболее часто параметром t является время.
Уравнения прямой, проходящей через две точки
Пусть прямая L проходит через точки 
. Составим канонические уравнения этой прямой. Для этого за направляющий вектор 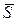примем вектор 
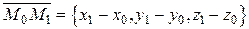, соединяющий две заданные точки, т.е. 
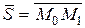. В качестве фиксированной точки возьмем любую из заданных, например М 0. Поэтому из канонических уравнений имеем
.
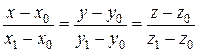Пример. Написать уравнения прямой, проходящей через точки 
и 
.
Подставим координаты точек в уравнения, получим
.
Угол между двумя прямыми
Пусть в пространстве даны две прямые
,
с направляющими векторами 
. Тогда j – угол между ними, равен углу, образованному векторами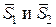 
. Поэтому
.
Угол между прямой и плоскостью
|
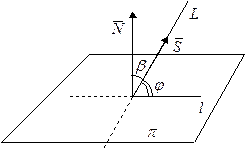
Углом j между прямой L, заданной уравнением 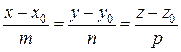и плоскостью p, заданной уравнением
,
называется угол между прямой L и ее проекцией на плоскость l.
Т.к.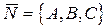 
– вектор, перпендикулярный плоскости p, то 
и 
. Из скалярного произведения 
– направляющего вектора прямой, находим
.
Следовательно 
.
Точка пересечения прямой и плоскости
Подставим параметрические уравнения прямой
в уравнение плоскости вместо x, y, z. Найдем значение параметра t, соответствующее точке пересечения, а затем, подставив его в параметрические уравнения, определим координаты точки пересечения 
.
Прямая на плоскости
Различные виды уравнений прямой на плоскости
Рассуждая аналогично, как в разделе “Прямая в пространстве”, можно написать следующие уравнения прямой l на плоскости Oxy.
Каноническое уравнение прямой
,
где 
– точка, через которую проходит прямая;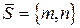 
– направляющий вектор прямой.
Уравнение прямой, проходящей через две точки
,
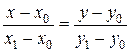где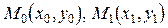 
– точки, через которые проходит прямая.
Общее уравнение прямой
Прямую на плоскости Oxy можно задать еще как пересечение двух плоскостей
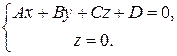
откуда 
. Обычно для обозначения свободного члена используют букву С и общее уравнение прямой записывают так:
Коэффициенты А и В являются компонентами вектора 
, нормального к данной прямой.
|
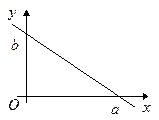
