При наличии в цепи только одного источника э.д.с. внешнюю по отношению к источнику, часть электрической цепи можно в большинстве случаев рассматривать как смешанное (последовательно-параллельное) соединение резистивных элементов. Расчет таких цепей проводят путем преобразования цепи до эквивалентного сопротивления. Определяют ток в ветви с источником э.д.с., а затем, используя закон Ома, рассчитывают токи в остальных ветвях.
ПРИМЕР 1.2.1. (свертывание)
Дано: 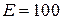 В;
В;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 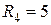 Ом;
Ом;
 Ом.
Ом.

Определить:  ,
,  ,
, 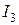 ,
,  ,
,  .
.
Решение: Резисторы  и
и 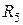 соединены параллельно, их эквивалентное сопротивление
соединены параллельно, их эквивалентное сопротивление  Ом
Ом

Резисторы  и
и 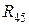 последовательны, находим их эквивалентное сопротивление
последовательны, находим их эквивалентное сопротивление  Ом.
Ом.

 и
и 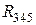 параллельны, их общее сопротивление
параллельны, их общее сопротивление 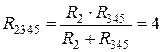 Ом.
Ом.

Определяем ток  :
:  А.
А.
По закону Ома рассчитаем напряжение 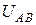 :
:  , тогда
, тогда  А.
А.
Ток 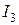 можно определить по I закону Кирхгофа:
можно определить по I закону Кирхгофа:  А.
А.
Для определения токов  и
и  найдем по закону Ома
найдем по закону Ома  :
:  , тогда
, тогда  А;
А; 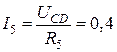 А.
А.
Напряжение  можно не находить, подставив в формулы для нахождения
можно не находить, подставив в формулы для нахождения  и
и  значения
значения 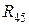 .
.
 А,
А,  А.
А.
1.2.1. Дано: 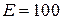 В;
В;  Ом;
Ом;  Ом;
Ом;  Ом.
Ом.
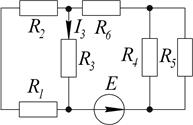
Определить токи в сопротивлениях.
1.2.2. Дано: 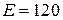 В;
В;  Ом;
Ом;  Ом;
Ом; 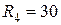 Ом;
Ом; 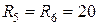 Ом.
Ом.

Определить токи в сопротивлениях.
1.2.3. Дано:  A;
A;  Ом;
Ом;  Ом;
Ом;  Ом.
Ом.

Определить токи в сопротивлениях.
1.2.4. Дано:  В;
В;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 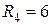 Ом
Ом

Определить токи в ветвях.
1.2.5. Дано:  В;
В;  Ом;
Ом; 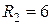 Ом;
Ом;  Ом;
Ом; 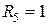 Ом;
Ом;  Ом;
Ом;  Ом;
Ом;

Определить распределение токов в схеме.
1.2.6. Дано:  А;
А;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 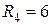 Ом.
Ом.

Определить токи в ветвях.
1.2.7. Дано:  В;
В;  Ом;
Ом;  Ом;
Ом; 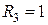 Ом;
Ом; 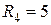 Ом.
Ом.

Определить напряжение  .
.
Закон Ома для активного участка цепи
Закон Ома для активного участка цепи между точками а и в имеет вид:
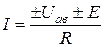 .
.
На основании второго закона Кирхгофа напряжение участка цепи и ЭДС берутся со знаком «+», если их направление совпадает с направление тока, и со знаком «-», если они направлены противоположно току.
ПРИМЕР 1.3.1
Дано:  В;
В;  В;
В;  В;
В;  Ом;
Ом;  Ом.
Ом.
Определить 
. 
 (А).
(А).
ЗАДАЧИ
1.3.1. Дано:  Ом;
Ом;  Ом;
Ом;  В;
В;  A.
A.

Определить  .
.
1.3.2. Дано:  Ом;
Ом;  Ом;
Ом; 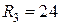 Ом;
Ом;  Вт.
Вт.
Определить  .
.

1.3.3. Дано:  Ом;
Ом;  Ом;
Ом;  В;
В; 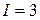 А.
А.
Определить  ,
,  .
.

1.3.4. Дано:  Ом. Показания амперметров:
Ом. Показания амперметров:  А;
А;  A.
A.

Определить  .
.
1.3.5. Дано:  Ом;
Ом;  Ом;
Ом;  В;
В;  В;
В;  В;
В;  В.
В. 
Определить ток в цепи.
1.3.6. Дано:  Ом;
Ом;  Ом;
Ом;  В;
В;  В;
В; 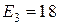 В;
В;  A.
A.

Определить  .
.
1.3.7. Дано:  B;
B;  Ом;
Ом;  Ом;
Ом; 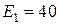 В;
В;  В;
В;  В;
В;  В
В
. 
Определить ток в цепи.
1.3.8.Дано:  Ом;
Ом;  Ом;
Ом; 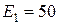 В;
В;  В;
В;  В;
В;  А
А
. 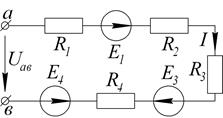
Определить  по закону Ома для участка цепи.
по закону Ома для участка цепи.
1.3.9. Дано:  B;
B; 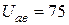 B;
B;  Ом;
Ом;  .
.

Определить  ;
; 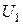 ;
;  ;
;  .
.
1.3.10. Дано:  Ом;
Ом;  Ом; вольтметр при замкнутом ключе показывает 60 В, при разомкнутом – 80 В.
Ом; вольтметр при замкнутом ключе показывает 60 В, при разомкнутом – 80 В.

Определить  .
.
1.3.11. Дано: Потребляемая мощность 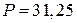 кВт;
кВт;  B;
B;  Ом;
Ом;  Ом.
Ом.
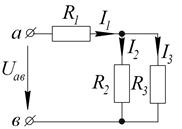
Определить токи  ,
, 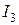 и мощности
и мощности  ,
, 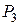 .
.
1.3.12. Дано:  Ом;
Ом;  Ом;
Ом; 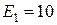 В;
В;  В;
В;  В;
В;  А.
А.
Определить  .
.
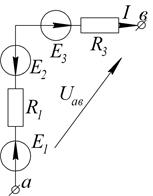
1.3.13. Дано:  Ом;
Ом;  Ом;
Ом; 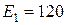 В;
В;  В.
В.
Определить напряжение между точками а и в.

1.3.14. Дано:  Ом;
Ом;  A;
A;  B
B
. 
Определить  .
.
Законы Кирхгофа
Первый закон Кирхгофа. Алгебраическая сумма токов, сходящихся в узле, равна нулю:

Ток, подходящий к узлу, берется со знаком «+», отходящий от узла, - со знаком «-».
Второй закон Кирхгофа. Алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС в этом контуре:
 .
.
В каждую из сумм соответствующие слагаемые входят со знаком «+», если их направления совпадают с направлением обхода контура, и со знаком «-», если их направления не совпадают с ним.
Для составления уравнений по законам Кирхгофа необходимо: выбрать произвольно направления токов в ветвях и выбрать положительные направления обхода контуров.
Количество уравнений определяется количеством неизвестных токов.
Число уравнений по первому закону Кирхгофа на единицу меньше числа узлов:

По второму закону Кирхгофа составляется недостающее число уравнений, равное числу независимых контуров или ветвей без источников тока (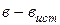 ) за вычетом числа уравнений, составленных по первому закону:
) за вычетом числа уравнений, составленных по первому закону:

При составлении уравнений по второму закону независимые контуры выбираются так, чтобы в каждый из них входила новая ветвь, исключая ветви с источниками тока.
ПРИМЕР 1.4.1.
Дано: 
Cоставить уравнения по законам Кирхгофа для определения неизвестных токов.

Решение:
Произвольно выбираем направление токов в ветвях и направление обхода контуров. В схеме шесть ветвей. Необходимо составить систему из  уравнений.
уравнений.
По первому закону составляем  уравнения.
уравнения.
Для узла 1:  .
.
Для узла 2:  .
.
Для узла 3: 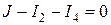 .
.
Недостающие два уравнения составляем по второму закону Кирхгофа:


ПРИМЕР 1.4.2
Дано: 





Составить уравнения по законам Кирхгофа и определить токи в ветвях.

По первому закону составляем  уравнения.
уравнения.
Для узла 1:  .
.
Для узла 2: 
Для узла 3:  .
.
Для узла 4: 
Недостающие пять уравнений составляем по второму закону Кирхгофа для явно выраженных контуров:
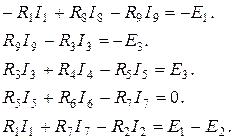
Запишем эти уравнения в виде удобном для записи их в матричной форме

Матричная форма записи системы уравнений: R×I=E.
Порядок решения заданной системы уравнений:
1. Установите режим автоматических вычислений.
2. Введите матрицу системы и матрицу - столбец правых частей.
3. Вычислите решение системы по формуле 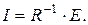
4. Проверьте правильность решения умножением матрицы системы на вектор - столбец решения.
5. Найдите решение системы с помощью функции lsolve и сравните результаты вычислений.
Ниже приведен фрагмент решения этой системы уравнений в программе Mathcad.
Зададим матрицу системы 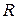 и матрицу - столбец
и матрицу - столбец 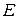 правой части.
правой части.
Надо найти матрицу - столбец неизвестных токов 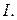

Вычислим решение системы по формуле  :
:
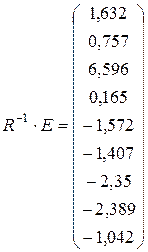 .
.
Где:  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
.
Решим систему с помощью функции lsolve и сравним результат с решением 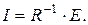

Заданная система уравнений решена правильно.
1.4.1.Составить уравнения по законам Кирхгофа для определения токов.
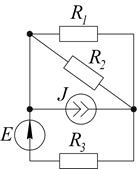

Определить  .
.
1.4.2. Дано:  Ом;
Ом;  Ом;
Ом;  В.
В.

Определить  ,
,  , указать режим работы данной цепи.
, указать режим работы данной цепи.

Определить  .
.
1.4.3. Дано:  Ом;
Ом;  В.
В.
Определить показания вольтметра, указать режим работы данной цепи.

Определить  .
.
1.4.4. Дано:  А;
А;  А;
А;  А.
А.
Определить  , указать режим работы данной цепи.
, указать режим работы данной цепи.

Определить  .
.
1.4.5. Дано:  Ом;
Ом;  Ом;
Ом;  В;
В;  В.
В.
Определить показания вольтметра.


Определить токи 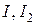 , если
, если 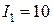 мА;
мА;  В;
В;  кОм;
кОм; 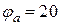 В;
В; 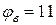 В.
В.

1.4.6. Определить  .
.
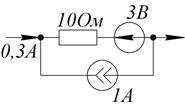
Определить мощность, отдаваемую источником тока.
1.4.7. Определить  .
.


Определить  .
.
Баланс мощностей
В любой электрической цепи должен соблюдаться энергетический баланс – баланс мощностей: алгебраическая сумма мощностей всех источников энергии равна арифметической сумме мощностей всех приемников энергии:
 .
.
Мощность источника ЭДС положительна, если ток в ветви с источником совпадает по направлению с ЭДС, такой источник является генератором.

Мощность источника ЭДС отрицательна, если ток в ветви с источником направлен противоположно ЭДС, в этом случае источник потребляет энергию.

При определении мощности источника тока напряжение  берется как разность потенциалов между узлом, к которому подходит ток источника
берется как разность потенциалов между узлом, к которому подходит ток источника  и узлом, от которого он отходит.
и узлом, от которого он отходит.

Метод контурных токов
При расчете методом контурных токов полагают, что в каждом независимом контуре течет неизвестный контурный ток, а источники тока создают известные контурные токи. Относительно неизвестных контурных токов составляют систему уравнений вида:

где  - контурные токи;
- контурные токи;
 - собственные сопротивления контуров;
- собственные сопротивления контуров;
 - сопротивления смежной ветви между контурами.
- сопротивления смежной ветви между контурами.
Сопротивление смежной ветви между «k» и «m» контурами ( ) входит в уравнение со знаком «+», если направления контурных токов
) входит в уравнение со знаком «+», если направления контурных токов  и
и  вдоль этой ветви одинаковы, и со знаком «-», если их направления противоположны.
вдоль этой ветви одинаковы, и со знаком «-», если их направления противоположны.
 - контурные ЭДС, равные алгебраической сумме э.д.с. этого контура. В них со знаком «+» входят те ЭДС, направления которых совпадают с обходом контура.
- контурные ЭДС, равные алгебраической сумме э.д.с. этого контура. В них со знаком «+» входят те ЭДС, направления которых совпадают с обходом контура.
Токи в ветвях находят как суперпозицию контурных токов.
Если схема содержит не только источники ЭДС., но и источники тока, то полагают, что ток источника тока замыкается по любым ветвям так, что вместе с ветвью источника создается замкнутый контур. Падение напряжения, вызванное током такого источника на каждом из сопротивлений контура, учитывается при записи левой части уравнений. Эти напряжения можно также учесть с обратным знаком в правой части уравнений.
ПРИМЕР 1.6.1
Дано:  В;
В;  А;
А;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом.
Ом.
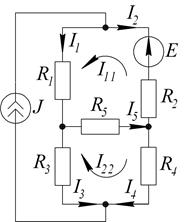
Определить токи в ветвях методом контурных токов
. 
Решение:
В схеме 6 ветвей, 4 узла, 1 источник тока. Число уравнений, которые необходимо составить методом контурных токов: 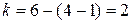 .
.
Задаем направление контурных токов  и
и  , полагая, что ток источника тока замыкается по резисторам
, полагая, что ток источника тока замыкается по резисторам  и
и  .
.
Составляем систему уравнений:

Подставляем числовые значения:

Решая эти уравнения, находим контурные токи:
 А,
А,
 А.
А.
Искомые токи: 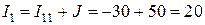 A;
A;
 А;
А;
 А;
А;
 А;
А;
 А.
А.
Составим уравнение баланса мощностей:

 .
.
 Вт,
Вт,
 Вт.
Вт.
 , пусть
, пусть  , тогда
, тогда  В.
В.
1.6.1. Составить уравнения для расчета цепи методом контурных токов.
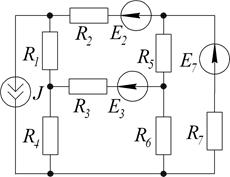
Дано:  Ом;
Ом;  Ом;
Ом; 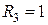 Ом;
Ом;  Ом;
Ом; 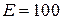 В;
В;  А.
А.
Определить токи в ветвях методом контурных токов.

1.6.2. Составить уравнения для расчета цепи методом контурных токов.


Дано:  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  В;
В;  А.
А.
Определить токи в ветвях методом контурных токов.
1.6.3. Составить уравнения для расчета цепи методом контурных токов.

Дано:  Ом;
Ом;  Ом;
Ом; 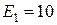 В;
В;  В;
В; 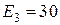 В;
В;  А.
А.
Определить токи в ветвях методом контурных токов.

1.6.4. Составить уравнения для расчета цепи методом контурных токов.
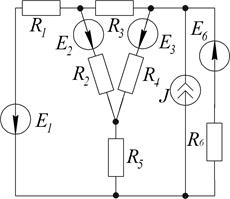

Дано:  Ом;
Ом; 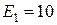 В;
В;  В;
В; 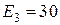 В;
В; 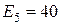 В;
В;  А.
А.
Определить токи в ветвях методом контурных токов.
1.6.5. Составить уравнения для расчета цепи методом контурных токов.


Дано:  Ом;
Ом;  Ом;
Ом;  В;
В;  В;
В;  А.
А.
Определить токи в ветвях методом контурных токов.
1.6.6. Составить уравнения для расчета цепи методом контурных токов.


Дано:  Ом;
Ом;  А;
А;  Ом;
Ом; 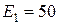 В;
В;  В.
В.
Определить токи в ветвях методом контурных токов.
1.6.7. Составить уравнения для расчета цепи методом контурных токов.


Дано:  Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 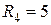 Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 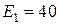 В;
В;  В;
В;  В;
В;  А;
А;  А.
А.
Определить токи в ветвях методом контурных токов.
Потенциальная диаграмма
Потенциальная диаграмма – это график распределения потенциалов вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с точки, потенциал которой принимают равным нулю, по оси ординат - потенциалы. Каждой точке рассматриваемого контура соответствует своя точка на потенциальной диаграмме.
ПРИМЕР 1.7.1.
Дано:  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 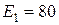 В;
В; 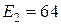 В;
В;  А;
А;  А;
А; 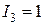 А.
А.
Построить потенциальную диаграмму для контура авсdа.

Решение: Подсчитаем суммарное сопротивление контура авсdа 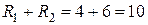 Ом и выберем масштабы по оси ординат. Точку а помещаем в начало координат. Определяем потенциалы в, с, d и их координаты.
Ом и выберем масштабы по оси ординат. Точку а помещаем в начало координат. Определяем потенциалы в, с, d и их координаты.
Принимаем  . Токораспределение в схеме при заземлении одной точки не изменится, т.к. никаких новых ветвей при этом не образуется.
. Токораспределение в схеме при заземлении одной точки не изменится, т.к. никаких новых ветвей при этом не образуется.
 В,
В,  ;
;
 В,
В,  ;
;
 В,
В,  ;
;
 В,
В,  .
.

Метод узловых потенциалов
Метод расчета электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов. Число неизвестных в этом методе равно числу узлов минус один.
Потенциал одного узла схемы принимают равным нулю, для остальных составляют систему уравнений вида
 ,
,
где  - сумма проводимостей ветвей, сходящихся в узле к;
- сумма проводимостей ветвей, сходящихся в узле к;
 - сумма проводимостей ветвей, соединяющих узлы к и m, взятая со знаком «-»;
- сумма проводимостей ветвей, соединяющих узлы к и m, взятая со знаком «-»;
 - узловой ток узла к. Находится как алгебраическая сумма токов короткого замыкания всех ветвей, сходящихся в узле к. С плюсом берутся те токи, источники которых направлены к узлу к.
- узловой ток узла к. Находится как алгебраическая сумма токов короткого замыкания всех ветвей, сходящихся в узле к. С плюсом берутся те токи, источники которых направлены к узлу к.
Если между двумя узлами нет ветви, то соответствующая проводимость равна нулю.
После решения системы относительно потенциалов определяют токи в ветвях по закону Ома.
ПРИМЕР 1.8.1.
Дано:  Ом;
Ом;  Ом;
Ом; 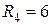 Ом;
Ом;  Ом;
Ом;  В;
В;  В;
В;  В;
В;  А.
А.
Определить токи методом узловых потенциалов
. 
Решение:
Примем потенциал узла 4 равным нулю:  , тогда потенциал
, тогда потенциал  В.
В.
Составим уравнения для узлов 1 и 2 (при этом учтем, что проводимость ветви, соединяющей узлы 1 и 2,  ):
):


Подставляем числовые значения:
 В;
В;
 В
В
Токи в ветвях находим по закону Ома:
 А;
А;
 А;
А;
 А;
А;
 А.
А.
Ток  находим по первому закону Кирхгофа, примененному к узлам 3 или 4:
находим по первому закону Кирхгофа, примененному к узлам 3 или 4:  А или
А или  А.
А.
ЗАДАЧИ
1.8.1. а) Составить уравнения для расчета цепи методом узловых потенциалов.
б) Определить токи в ветвях методом узловых потенциалов, если  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 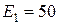 В;
В;  В;
В;  В;
В;  В.
В.

Дано:  Ом;
Ом;  Ом;
Ом; 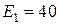 В;
В;  В;
В;  А.
А.
Определить токи методом узловых потенциалов. Построить потенциальную диаграмму для контура 1‑2‑3‑4‑1.
1.8.2. а) Составить уравнения для расчета цепи методом узловых потенциалов.
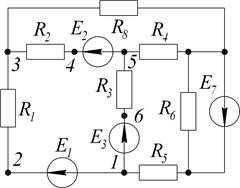

б) Определить токи в ветвях методом узловых потенциалов, если  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 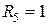 Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 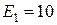 В;
В;  В;
В;  В;
В;  В. Построить потенциальную диаграмму для контура 1-2-3-4-5-6.
В. Построить потенциальную диаграмму для контура 1-2-3-4-5-6.
Дано:  Ом;
Ом;  В;
В;  В;
В;  А.
А.
Определить токи в ветвях методом узловых потенциалов.

1.8.3. а) Составить уравнения для расчета цепи методом узловых потенциалов.
б) Определить токи в ветвях методом узловых потенциалов, если 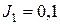 A;
A; 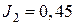 A;
A; 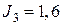 A;
A;  Ом;
Ом; 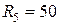 Ом;
Ом;  Ом;
Ом;  См;
См;  См;
См;  См;
См;  В.
В.
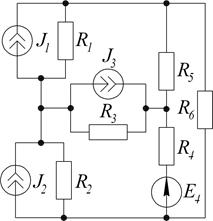
Дано:  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  В;
В;  В;
В; 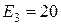 В.
В.
Определить токи в ветвях методом узловых потенциалов.

1.8.4. а) Составить уравнения для расчета цепи методом узловых потенциалов.
б) Определить токи в ветвях методом узловых потенциалов, если  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 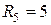 Ом;
Ом;  Ом;
Ом; 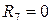 Ом;
Ом; 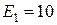 В;
В;  В;
В;  В;
В;  В;
В;  А
А

Дано:  Ом;
Ом; 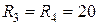 Ом;
Ом;  В;
В;  В;
В;  В.
В.
Определить токи методом узловых потенциалов. Построить потенциальную диаграмму для контура 1-2-3-4-1.

1.8.5. Определить токи в ветвях методом узловых потенциалов, если  См;
См;  См;
См;  См;
См;  См;
См;  См;
См;  В;
В;  В;
В;  В.
В.
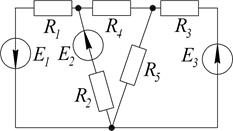
Дано:  Ом;
Ом;  Ом;
Ом;  В;
В;  В;
В;  A.
A.

Определить токи в ветвях методом узловых потенциалов.
1.8.6. а) Составить уравнения для расчета цепи методом узловых потенциалов.

б) Рассчитать токи в ветвях, если  Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 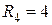 Ом;
Ом;  Ом;
Ом;  В;
В; 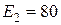 В;
В;  В;
В;  А.
А.
Дано:  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  А;
А;  В;
В;  В.
В.

Методом узловых потенциалов найти токи  и
и 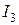 .
.
1.8.7. а) Составить уравнения для расчета цепи методом узловых потенциалов.
б) Рассчитать токи в ветвях методом узловых потенциалов, если  Ом;
Ом;  Ом;
Ом;  Ом;
Ом;  Ом;
Ом; 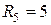 Ом;
Ом;  Ом;
Ом;






