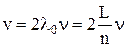,
где L – некоторое расстояние, на котором наблюдается стоячая волна;
n – число узлов;
n – частота колебаний.
Бегущие волны – волны, которые переносят в пространстве энергию.
Уравнение плоской прямой бегущей волны, распространяющейся со скоростью v в направлении x, выражение, которое определяет смещение колеблющейся точки как функцию ее координат и времени:
,
где x – смещение от положения равновесия точки, находящейся на расстоянии x от источника гармонических колебаний;
x0 – амплитуда колебаний;
w – циклическая частота колебаний;
j0 – начальная фаза колебаний.
Уравнение плоской обратной бегущей волны:
.
Связь между разностью фаз двух точек бегущей волны и разностью хода (x2 – x1), т.е. разностью расстояний этих точек от источника колебаний:
.
Волновое уравнение плоской волны, распространяющейся вдоль оси X, дифференциальное уравнение второго порядка в частных производных:
.
Волновое уравнение плоской волны, распространяющейся в трехмерном пространстве:
,
где 
– оператор (лапласиан).
Скорость звука в газах
,
где p – давление газа, не возмущенного волной;
r – плотность газа, не возмущенного волной;
– отношение молярной теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме.
Амплитуда звукового давления Dp0 и амплитуда скорости v 0 частиц в звуковой волне связаны соотношением
.
Интенсивность звука I, выраженная через амплитуду звукового давления – энергия, переносимая звуковой волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны:
,
где r – плотность газа.
Уровень интенсивности звука (в децибелах) определяется формулой
,
где I – интенсивность данного звука;
I0 = 10–12 Вт/м2 – интенсивность звука на пороге слышимости при стандартной частоте n = 1 кГц.
Уровень громкости звука (в фонах) вычисляется по формуле
,
где IN – интенсивность звука стандартной частоты n = 1 кГц, равногромкого с исследуемым звуком.
Явление Доплера – если источник и приемник звука перемещаются относительно среды, в которой распространяется звук, то частота звуковых колебаний n', регистрируемая приемником звука, связана с частотой собственных колебаний n источника соотношением
,
где c, u, v – скорости соответственно звука, его источника и приемника.
Примечание. Записанная формула относится к случаю, если источник и приемник звука движутся по одной прямой. При этом величины u, v – алгебраические: u > 0, если источник движется к приемнику; u < 0, если источник удаляется от приемника. Аналогично v > 0, если приемник приближается к источнику; v < 0, если приемник движется от источника.
Вектор плотности потока энергии волны – физическая величина, модуль которой равен энергии DW, переносимой волной за единицу времени (Dt = 1) через единичную площадку, расположенную перпендикулярно направлению распространения волны (DS^):
; 
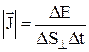= u v; J = u×v,
где u – плотность энергии в каждой точке среды, среднее значение которой вычисляется по формуле 
;
ρ – плотность среды;
x0 – амплитуда волны;
w – круговая (циклическая частота);
v – фазовая скорость (скорость перемещения фазы волны).
