.
Принцип относительности Галилея (в классической механике) – никакие опыты, проводимые в инерциальных системах отсчета с механическими приборами, не позволяют установить, покоится система отсчета или движется равномерно и прямолинейно по отношению к другой инерциальной системе отсчета. Предполагается, что время не зависит от относительного движения систем отсчета.
Преобразования Галилея определяют положение произвольной материальной точки в двух инерциальных системах отсчета, одна из которых движется со скоростью v o относительно другой (при условии, если направление скорости v 0 совпадает с направлением r o):
r = r ' + r 0 = r ' + v ot; t = t',
где r и r ' – радиус-векторы, определяющие положение материальной точки в неподвижной и подвижной системе отсчета в данный момент времени;
r o – радиус вектор, определяющий положение начала координат системы К' (подвижной) в системе К (неподвижной).
В проекциях на оси координат в произвольный момент времени t положение выбранной точки в системе К можно определить так:
x = x' + v0xt, x' = x – v0xt,
у = у' + v0уt, у' = у – v0уt,
z = z' + v0zt, z' = z – v0zt,
t = t'. t = t'.
Ковариантные или инвариантные уравнения – уравнения, обе части которых при переходе от одной системы координат к другой преобразуются одинаково и сохраняют свой вид во всех инерциальных системах отсчета.
Закон сложения скоростей в классической механике:
v = v ' + v 0.
Относительное расстояние между выбранными точками пространства в системах отсчета определяется соотношением – они абсолютны, т.е. инвариантны:
1) в подвижной:
;
2) в неподвижной:
.
Инварианты преобразований – инвариантные величины (расстояния между телами (точками), промежутки времени между событиями, относительные скорости тел, ускорения).
Вращательное движение твердого тела вокруг неподвижной оси – движение, при котором какие-либо две его точки остаются неподвижнымив процессе движения. Прямая, проходящая через эти точки, – ось вращения; все остальные точки твердого тела описывают окружности в плоскостях, перпендикулярных к оси вращения, центры которых лежат на этой оси (рис. П1.3).
Основные кинематические характеристики вращательного движения (рис. П1.4):
1) угол поворота D j – угол, отсчитанный между двумя последовательными положениями радиуса R;
2) угловая скорость w – векторная физическая величина, показывающая, как изменяется угол поворота Dj в единицу времени, численно равная первой производной от угла поворота по времени. Вектор угловой скорости направлен вдоль оси вращения в сторону, определяемую правилом правого винта:
.
3) угловое ускорение e – векторная физическая величина, характеризующая изменение угловой скорости в единицу времени, численно равная первой производной от угловой скорости по времени или второй производной от угла поворота по времени Направление вектора углового ускорения совпадает с направлением вектора угловой скорости в случае ускоренного вращения и противоположно – в случае замедленного:
Период вращения (T) – время, в течение которого тело совершает один полный оборот.
Частота вращения (n) – число оборотов, совершаемых в единицу времени.
Круговая (циклическая) частота ω – число оборотов, совершаемых за время, равное 2π.
Связь между периодом, частотой и круговой частотой:
ω = 2π n = 2π / T; n = 1 / T.
Связь между линейными и угловыми скоростями и ускорениями
Колебательные движения (колебания) – движения или процессы, обладающие повторяемостью во времени.
Гармонические колебания (простейший вид колебаний) – движения, при которых смещение материальной точки (тела) от положения равновесия изменяется по закону синуса или косинуса (рис. П1.5):
x = x0×sin (w0t + j0),
где x – смещение это удаление материальной точки от положения равновесия в данный момент времени t;
x0 – амплитуда колебаний это максимальное удаление материальной точки от положения равновесия;
(wt + j0) – фаза колебаний. Периодически изменяющийся аргумент функции, описывающей колебательный или волновой процесс. Определяет положение материальной точки в данный момент времени t;
j0 – начальная фаза колебаний. Определяет положение материальной точки в начальный момент времени t = 0;
w = 2p / T = 2p n – круговая (циклическая) частота колебаний;
T – период колебаний;
n – частота колебаний.
Скорость при гармоническом колебательном движении (колебательная скорость) – физическая величина, которая показывает, как изменяется смещение в единицу времени, численно равная первой производной от смещения по времени:
.
Ускорение при гармоническом колебании – физическая величина, которая показывает, как изменяется скорость в единицу времени, численно равная первой производной от скорости или второй производной от смещения по времени:
.
Знак «минус» означает, что ускорение направлено в сторону, противоположную смещению.
Сложение гармонических колебаний одного направления (рис. П1.6) с одинаковыми амплитудами и частотами (x01 = x02; w1 = w2 = = w), но разными начальными фазами (j02 ¹ j01) проводят аналитически. Уравнение результирующего колебания имеет вид
где 
– амплитуда результирующего колебания;
– фаза результирующего колебания.
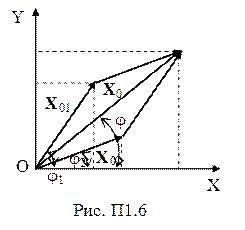
Биения возникают при сложение колебаний одного направления (рис. П1.7), с одинаковыми амплитудами (x02 = x01), начальными фазами j01 = j02 = 0 и круговыми частотами, мало отличающимися друг от друга (w1» w2). Уравнения таких колебаний имеют вид
x1 = x01×sin w1t; x2 = x01×sin w2t.
Уравнение результирующего колебания:
,
где 
– амплитуда результирующего колебания, которая зависит от Dw = w1 – w2 – разности частот складываемых колебаний;
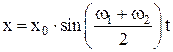– смещение результирующего колебания, изменяющееся по гармоническому закону.
Частота и период результирующего колебания:
Частота и период изменения амплитуды в этом случае:
Сложение взаимно перпендикулярных колебаний приводит к тому, что траектория движения представляет собой замкнутые фигуры, называемые фигурами Лиссажу (рис. П1.8):
1) сложение колебаний с одинаковыми частотами (w1 =w2 =w), различными амплитудами (x 0 ¹ y 0) с начальными фазами j1 = j2 = 0 – результирующее колебание – гармоническое. Траектория движения – прямая линия, уравнение которой имеет вид
y = (y0/x0)×x.
2) сложение колебаний, начальные фазы j1 и j2 которых отличаются на p/2 (j1 – j2 = p/2) – результирующее колебание – гармоническое. Траектория движения – эллипс (при равных амплитудах x0 = y0 – траектория результирующего движения – окружность) с полуосями, равными x0 и y0, уравнение которого
(y/y0)2 + (x/x0)2 = 1;
3) сложение колебаний, периоды которых относятся как целые числа – через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка возвращается в начальное положение – получаются фигуры Лиссажу более сложной формы.
Динамика изучает движение и взаимодействия тел совместно с причинами, обусловливающими тот или иной характер движения и взаимодействия.
Основная задача динамики – для данного тела по известной силе найти его ускорение и, наоборот, по известному ускорению найти результирующую силу, действующую на тело.
Масса m – физическая величина, характеризующая количество вещества, инертность, гравитационные свойства и энергию материального тела. Массу тела, определяющую его инертные свойства, называют инертной массой.
Центр масс (или центр инерции) системы – воображаемая точка С, положение которой характеризует распределение массы этой системы и определяется радиус-вектором:
,
где mi и r i – соответственно масса и радиус-вектор i-й материальной точки;
n – число материальных точек в системе.
Скорость центра масс
,
где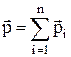 
– полный импульс системы.
Импульс p ( количество движения) – физическая величина, описывающая свойства движущихся тел, равная произведению массы на скорость:
p = m v.
Полный импульс системы равен произведению массы системы на скорость ее центра масс:
p = m v c.
Покой – частный случай равномерного прямолинейного движения со скоростью v = 0.
Инерция – свойство тел сохранять состояние покоя или равномерного прямолинейного движения.
Инерциальные системы отсчета – системы отсчета, в которых выполняются первый и второй законы Ньютона (их уравнения и все следствия).
Неинерциальная система отсчета – система отсчета, движущаяся по отношению к инерциальной системе отсчета с ускорением.
Первый закон Ньютона: «Всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока равнодействующая всех приложенных сил равна нулю».
Сила F – векторная физическая величина, характеризующая воздействие одних тел на другие. В результате действия силы изменяется состояние движения тела (тело приобретает ускорение) или тело деформируется.
Сила F в механике – мера механического действия на данное материальное тело (данную материальную точку) других тел (других материальных точек) или полей.
Закон независимости действия сил: при действии на тело нескольких сил каждая из них сообщает телу такое же ускорение, какое она сообщила, если бы действовала одна.
Принцип суперпозиции сил – допущение, согласно которому результирующий эффект сложного процесса воздействия представляет собой сумму эффектов, вызываемых каждым воздействием в отдельности, при условии, что воздействия взаимно не влияют друг на друга. Он применим к системам, поведение которых описывается линейными соотношениями.
Сложение нескольких сил, действующих одновременно на материальную точку (тело, систему) производится геометрически. Действие нескольких сил можно заменить действием одной силы, которая называется равнодействующей (рис. П1.9):
;
.
Условие равновесия сил:
.
На рисунке П1.10 показано равновесие сил, лежащих в одной плоскости, действующих на материальную точку. Рисунок П1.11 соответствует равновесию сил, не лежащих в одной плоскости, действующих на материальную точку. Две силы, действующие под углом на одну материальную точку, не могут уравновесить друг друга ни при каких условиях.
Так же и три силы, не лежащие в одной плоскости, не могут уравновесить друг друга ни при каких условиях (рис. П 1.12).
Ускорение в динамике a – результат действия силы.
Ускорение материальной точки в инерциальных системах отсчета К и К' одинаково:
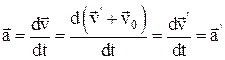; a = a '.
Второй закон Ньютона – изменение импульса пропорционально приложенной силе и направлено вдоль прямой, по которой действует данная сила (основное уравнение движения в классической динамике):
.
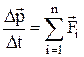При Dt ® 0
.
При v << c ускорение, с которым движется тело, прямо пропорционально приложенной силе и обратно пропорционально массе тела:
.
В случае переменной массы
,
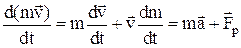где 
– реактивная сила.
При движении по кривой результирующая сила может быть разложена на две составляющие (рис. П 1.13):
; 
,
где R – радиус кривизны траектории;
– тангенциальная составляющая (касательная сила);
– нормальная составляющая (центростремительная сила).
Основной закон классической динамики – инвариантен при переходе от одной инерциальной системы к другой, при этом
ma = F; m a ' = F '; F = F '.
Третий закон классической динамики – силы, с которыми взаимодействуют два тела, равны по величине и противоположны по направлению. Силы действия и противодействия приложены к разным телам и никогда не уравновешивают друг друга (рис. П1.14):
F 12 = - F 21.
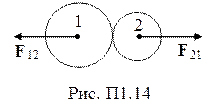
Импульс силы – мера действия силы за некоторый промежуток времени:
.
Силы инерции обусловлены ускоренным движением системы отсчета по отношению к неподвижной системе. Различают:
1) силы, действующие на тело при ускоренном поступательном движении системы отсчета (рис. П1.15):
m a’ =m a + F ин,
где a’ – ускорение тела в неинерциальной системе отсчета;
a – ускорение тела в инерциальной системе отсчета;
F ин – сила инерции.
2) силы, действующие на тело, покоящееся во вращающейся системе отсчета (рис. П 1.16):
,
где F ц – центробежная сила инерции;
w – угловая скорость вращающейся системы отсчета;
r’ – радиус-вектор тела относительно начала вращающейся системы отсчета;
R – перпендикулярная к оси вращения составляющая r’.
3) силы, действующие на тело, движущееся во вращающейся системе отсчета (рис. П1.17):
F к = 2m×[ v’ ω ],
где F к – сила Кориолиса;
v’ – скорость движения тела;
w – угловая скорость вращающейся системы отсчета.
Основной закон динамики для неинерциальных систем отсчета:
m a’= F + F ин + F ц+ F к,
где F, F ин, F ц, F к – ранее рассмотренные силы, действующие в неинерциальных системах отсчета.
Основная задача динамики вращательного движения – нахождение угловых ускорений, сообщаемых известными силами.
Момент инерции – скалярная физическая величина, характеризующая инертность тела при вращательном движении.
Момент инерции материальной точки относительно неподвижной оси вращения – физическая величина, равная произведению массы материальной точки на квадрат расстояния до оси или центра вращения (рис. П1.18):
DI = Dm×r2.
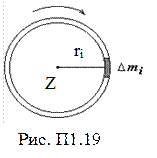
Момент инерции тела относительно оси z – физическая величина, равная сумме моментов инерции отдельных материальных точек тела относительно той же оси вращения (рис. П1.19):
; 
,
где mi – масса i-й точки;
ri – расстояние i-й точки до оси z;
ρ – плотность вещества, из которого состоит тело;
V – объем тела.
Теорема Штейнера – момент инерции тела относительно произвольной оси z равен сумме момента инерции того же тела I0 относительно оси, параллельной данной и проходящей через центр масс, и произведения массы тела m на квадрат расстояния между осями (а):
Iz = I0 + mа2.
На рисунке П1.20 представлено применение теоремы Штейнера к расчету момента инерции диска относительно оси ОО', параллельной оси О1О1'.
Главные оси инерции – три взаимно перпендикулярных свободных оси вращения тела произвольной формы, проходящие через его центр масс.
Момент импульса материальной точки относительно неподвижной оси вращения (L) – векторная физическая величина, модуль которой равен произведению модуля импульса на плечо (рис. П1.21):
ç L ê= êpê×l.
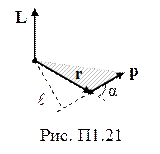
В векторной форме
L= [ r´p ] = [ r´ m v ],
где m – масса материальной точки;
v – скорость материальной точки;
l – плечо (кратчайшее расстояние от направления импульса до оси вращения).
Момент импульса системы относительно неподвижной оси вращения z – проекция на эту ось вектора L (момента импульса системы):
,
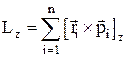где r i, p i – радиус-вектор и импульс i-й материальной точки;
n – общее число точек в системе.
Связь момента импульса тела с вектором угловой скорости ω и моментом инерции
L = I ω.
Момент силы относительно центра вращения или неподвижной оси вращения – векторная физическая величина, модуль которой равен произведению модуля силы на плечо (рис. П1.22):
ç M ç = ç F çl,
где l – плечо силы – кратчайшее расстояние от линии действия силы до центра вращения.
В векторной форме
M= [ r´F ].
Главный или результирующий момент сил относительно неподвижной оси вращения равен векторной сумме моментов слагаемых сил:
.
Моменты сил относительно осей, которые перпендикулярны и параллельны оси вращения, равны нулю.
Основной закон динамики вращательного движения твердых (недеформирующихся) тел, для которых I=const (второй закон динамики для вращательного движения):
M = I∙ ε; 
.
Импульс вращающего момента – произведение вращающего момента на время его действия:
M× dt = d L.
Осциллятор – физическая система, совершающая колебания; система, у которой величины, описывающие ее, периодически меняются с течением времени.
Гармонический осциллятор – механическая система, совершающая колебания около положения устойчивого равновесия, описывающие величины которой изменяются по гармоническому закону (закону синуса или косинуса).
Уравнение движения гармонического осциллятора:
; 
; 
,
где a = d2x/dt2 = –ω02x – ускорение материальной точки;
F – возвращающая сила, которая стремится вернуть систему в положение равновесия (F = –mω02x = –kx);
x – смещение;
k = mω02 – коэффициент возвращающей силы. Он численно равен возвращающей силе, вызывающей единичное смещение.
Решение уравнения движения гармонического осциллятора:
x = x0×sin (ω0t + φ0).
Уравнение гармонических колебаний в комплексном виде:
.
В теории колебаний принимается, что величина x равна вещественной части комплексного выражения, стоящего в этом выражении справа.
Дифференциальное уравнение гармонического колебательного движения:
.
Решением дифференциального уравнения гармонических колебаний является выражение вида
x = x0 sin (w0t + j0),
где k = m w02 – коэффициент возвращающей силы;
x – смещение материальной точки;
x0 – амплитуда колебаний;
w0 = 2p/Т = 2pn – круговая (циклическая частота);
n = 1/T – частота колебаний;
T – период колебаний;
j = (w0t + j0) – фаза колебаний;
j0 – начальная фаза колебаний.
Примеры гармонических осцилляторов:
а) пружинный маятник – тело массой m (рис. П1.23), подвешенное на пружине, совершающее гармоническое колебание.
Упругие колебания совершаются под действием упругих сил:
F= –k∙Dl,
где k = m wo2 – коэффициент жесткости;
Dl – относительное удлинение.
Уравнение движения пружинного маятника:
; 
,
где 
;
Dl – величина деформации.
Решение уравнения движения пружинного маятника:
Dl = (Dl)0×sin (ω0t + φ0).
Круговая частота, частота и период колебаний пружинного маятника:
; 
; 
;
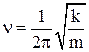б) физический маятник – твердое тело, совершающее гармоническое колебательное движение относительно оси, не совпадающей с центром масс (рис. П1.24).
Уравнение движения физического маятника:
.
Решение уравнения движения физического маятника:
j = j0×sin (ω0t + α),
где α – начальная фаза колебаний.
Круговая частота, частота и период колебаний физического маятника:
; 
; 
; 
,
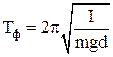где L = I/md – приведенная длина физического маятника – длина такого математического маятник, период колебаний которого равен периоду колебаний физического маятника;
I – момент инерции физического маятникa относительно оси колебаний;
m – масса физического маятника;
d – расстояние между осью колебаний и центром масс;
в) математический маятник – тело массой m, размерами которого можно пренебречь, подвешенное на невесомой, нерастяжимой нити (рис. П1.25).
Круговая частота, частота и период колебаний математического маятника:
; 
; 
.
Приведенная длина физического маятника – величина, численно равная длине такого математического маятника, период колебаний которого равен периоду колебаний физического маятника:
.
Крутильные колебания – колебания, совершающиеся под действием закручивающего момента, пропорционального углу закручивания (колебания диска, подвешенного на стальной нити):
M= – Da,
где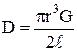 
– коэффициент крутильной жесткости;
G – модуль сдвига;
r – радиус нити;
l – длина нити.
