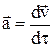 .
.
инематические уравнени€ движени€ в четырехмерной системе отсчета (по известному а (t) можно найти v (t) и S (t)):
 ,
, 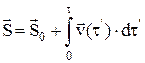 .
.
‘ормулы преобразовани€ координат при переходе из одной системы отсчета в другую (преобразовани€ √.ј. Ћоренца):
а) обратные:
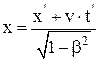 ; у = у'; z = z';
; у = у'; z = z'; 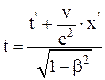 ;
;
б) пр€мые:
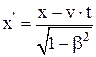 ; у = у'; z = z';
; у = у'; z = z'; 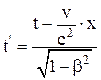 .
.
—ледстви€ из преобразований Ћоренца:
а) закон сложени€ скоростей (в частном случае, когда скорость u направлена вдоль оси OX):
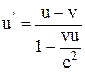 ;
;
б) сокращение продольных движущихс€ масштабов длин сокращени€ (Ћоренца):
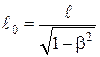 ;
; 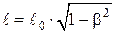 ,
,
где ℓ0 Ц длина стержн€ в той системе отсчета, в которой он покоитс€;
ℓ Ц длина стержн€ в системе отсчета, движущейс€ относительно стержн€;
в) замедление хода движущихс€ часов:
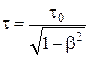 ;
; 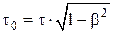 ,
,
где τ0 = t2' Ц t1' Ц промежуток времени, прошедший между этими событи€ми, в подвижной системе ';
τ = t2 Ц t1 Ц промежуток времени, прошедший между этими событи€ми, в неподвижной системе .
ѕервый закон Ќьютона в специальной теории относительности устанавливает существование в природе систем отсчета, сколь угодно близких к инерциальным системам отсчета. “акими системами отсчета €вл€ютс€ те, в которых свободное тело не имеет по отношению к ним ускорени€.
«ависимость массы от скорости
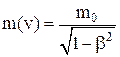 ,
,
где m Ц масса движущегос€ тела;
m0 Ц масса поко€.
инетическа€ масса
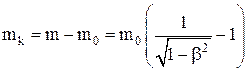 ,
,
где m Ц рел€тивистска€ (полна€) масса;
m0 Ц масса поко€;
mк Ц кинетическа€ масса.
ћасса системы не равна сумме масс, составл€ющих ее тел:
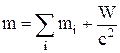 ,
,
где m Ц масса системы;
mi Ц масса изолированных тел, составл€ющих систему;
W Ц энерги€ взаимодействи€ изолированных тел.
»мпульс (вектор энергии-импульса) материальной точки
 ,
,
где m0 Ц масса тела в той системе отсчета, по отношению к которой тело покоитс€ (масса поко€);
v Ц скорость тела.
¬торой закон Ќьютона (уравнение движени€ материальной точки) в специальной теории относительности:
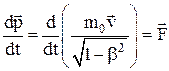 .
.
“ретий закон Ќьютона в специальной теории относительности:
F μ,n= ЦF n,μ,
где F μ,n и F n,μ Ц силы взаимодействи€ материальных точек в четырехмерной системе Ђпространство-врем€ї.
¬нутренн€€ энерги€ тела пропорциональна массе поко€ этого тела:
≈вн = m0×c2.
инетическа€ энерги€ тела
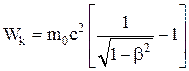 .
.
ѕолна€ энерги€ тела складываетс€ из внутренней энергии и кинетической энергии тела как целого:
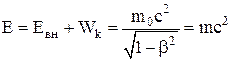 ,
,
где  Ц рел€тивистска€ масса.
Ц рел€тивистска€ масса.
Ёнерги€ св€зи системы каких-либо частиц Ц работа, затраченна€ на разделение системы на составл€ющие ее частицы и удаление их друг от друга на такое рассто€ние, на котором их взаимодействием можно пренебречь:
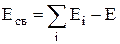 ,
,
где Eсв Ц энерги€ св€зи;
åEi Ц сумма энергий разделенных частиц системы;
E Ц энерги€ системы.
—умма масс разделенных частиц больше массы системы на величину энергии св€зи, деленную на c2:
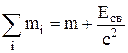 .
.
ƒефект массы Dm Ц разность между суммой масс частиц и массой системы:
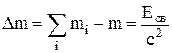 .
.
«акон взаимосв€зи массы и энергии:
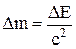 , E = mc2.
, E = mc2.
«акон изменени€ импульса-энергии материальной точки:
 .
.
«акон изменени€ энергии материальной точки:
|
|
|
 .
.
«акон изменени€ кинетической энергии тела:
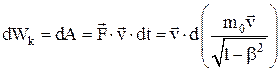 .
.
—оотношение, св€зывающее полную энергию и импульс рел€тивистской частицы (в векторной форме):
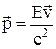 .
.
—в€зь между импульсом и полной энергией в скал€рной форме:
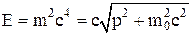 .
.
—в€зь между импульсом и кинетической энергией:
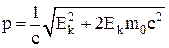 .
.
ƒл€ частиц с нулевой массой поко€ энерги€ пропорциональна импульсу:
E = c×p; p = E/c.
инетическа€ масса частиц, которые не обладают массой поко€, равна полной энергии:
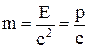 .
.
ѕриложение 2
ќсновы молекул€рной физики и термодинамики. ќсновные пон€ти€, определени€ и законы






