Постоянный электрический ток

 

Сила постоянного тока

I = q/t,

где q – заряд, прошедший через поперечное сечение проводника за время t.

Плотности тока

j = I/S,

где S – площадь поперечного сечения проводника.

Связь плотности тока со средней скоростью <υ> направлен­ного движения заряженных частиц

j = qn<υ>,

где q – заряд частицы; n – концентрация заряженных частиц.

Закон Ома:

а) для участка цепи, не содержащего ЭДС, где φ₁ – φ₂ = U – разность потенциалов (напряжение) на концах участка цепи; R – сопротивление участка;

б) для участка цепи, содержащего ЭДС, где – ЭДС источника тока; R – полное сопротивление участка (сумма внешних и внутренних сопротивлений);

в) для замкнутой (полной) цепи, где R – внеш­нее сопротивление цепи; R_i – внутреннее сопротивление цепи.

Законы Кирхгофа:

а) ∑ I_i = 0 – первый закон;

б) ∑ I_iR_i = ∑ – второй закон,

где ∑ I_i – алгебраическая сумма сил токов, сходящихся в узле; ∑ I_iR_i – алгебраическая сумма произведений сил токов на сопротивление уча­стков; ∑ e_i – алгебраическая сумма ЭДС.

Сопротивление R и проводимость G проводника

R = ρl/S, G=γS/l,

где ρ – удельное сопротивление; γ – удельная проводимость; l – длина проводника; S – площадь поперечного сечения проводника.

Сопротивление системы проводников:

а) R = ∑ R_i при последовательном соединении;

б) 1/R = ∑(1/R_i) при параллельном соединении, где R_i – сопро­тивление i-го проводника.

Работа тока

A = IUt, A = I²Rt, A = U²t/R.

Первая формула справедлива для любого участка цепи, на кон­цах которого поддерживается напряжение U, последние две – для уча­стка, не содержащего ЭДС.

Мощность тока

P = IU, P = I²R, P=U²/R.

Закон Джоуля – Ленца

Q = I²Rt.

Закон Ома в дифференциальной форме

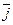= γ ,

где γ – удельная проводимость; – напряженность электрического поля; 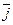– плотность тока.

 

Примеры решения задач

 

Пример 1. На тонком стержне длиной l = 20 см находится рав­номерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится то­чечный заряд q₁ = 40 нКл, который взаимодействует со стержнем с си­лой F = 6 мкН. Определить линейную плотность τ заряда на стержне.

Р е ш е н и е. Сила взаимодействия F заряженного стержня с точечным зарядом q₁ зависит от линейной плотности τ заряда на стержне. Зная эту зависимость, можно определить τ. При вычислении силы F следует иметь в виду, что заряд на стержне не является точеч­ным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим из стержня (рис. 1) малый участок dr с зарядом dq = τdr. Этот заряд можно рас­сматривать как точечный. Тогда, согласно закону Кулона,

Интегрируя это выражение в пределах от 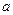до 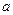+ , полу­чаем

 

откуда

Проверим, дает ли расчетная формула единицу линейной плот­ности электрического заряда. Для этого в правую часть формулы вме­сто символов величин подставим их единицы:

 

Найденная единица является единицей линейной плотности заряда.

Произведем вычисления:

Пример 2. По тонкому кольцу равномерно распределен заряд q = 40 нКл с линейной плотностью τ = 50 нКл/м. Определить напря­женность электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстоянии, равное половине радиуса.

 

 

Р е ш е н и е. Совместим координатную плоскость xOy с плос­костью кольца, а ось Oz – с осью кольца (рис. 2). На кольце выделим малый участок длиной dl. Так как заряд dq=τdl, находящийся на этом участке, можно считать точечным, то напряженность d электриче­ского поля, создаваемого этим зарядом, может быть записана в виде

 

где – радиус-вектор, направленный от элемента dl к точке А.

Разложим вектор d на две составляющие: d ₁, перпендику­лярную плоскости кольца (сонаправленную с осью Oz), и d ₂, парал­лельную плоскости кольца (плоскости xOy), т. е.

.

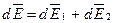Напряженность электрического поля в точке А найдем интегрированием:

где интегрирование ведется по всем элементам заряженного кольца. Заметим, что для каждой пары зарядов dq и dq` (dq = dq`), расположен­ных симметрично относительно центра кольца, векторы d ₂ и d ₂` в точке А равны по модулю и противоположны по направлению: d <sub>2</sub> = - d <sub>2</sub>`. Поэтому векторная сумма (интеграл) Составляю­щие d ₁ для всех элементов кольца сонаправлены с осью Oz (единич­ным вектором ), т. е. d ₁ = dE₁. Тогда

Так как и то

Таким образом,

Из соотношения q = 2πRτ определим радиус кольца R = q/(2πτ). Тогда

Модуль напряженности

(1)

Проверим, дает ли правая часть полученного равенства еди­ницу напряженности (В / м):

Выразим физические величины, входящие в формулу (1), в единицах СИ (τ = 5·10^-8 Кл/м, q=4·10^-8 Кл, ε₀ = 8,85·10^-12 Ф/м) и произ­ведем вычисления:

 

Пример 3. Две концентрические проводящие сферы радиу­сами R₁ = 6 см и R₂ = 10 см несут соответственно заряды q₁ = 1нКл и q₂ = - 0,5нКл. Найти напряженность Е поля в точках отстоящих от цен­тра сфер на расстояниях r₁ = 5 см, r₂ = 9 см, r₃ = 15 см. Построить гра­фик E(r).

 

Р е ш е н и е. Заметим, что точки, в которых требуется найти напря­женности электрического поля, лежат в трех областях (рис. 3): об­ласти I (r₁<R₁), области II (R₁<r₂<R₂), области III (r₂>R₂).

1. Для определения напряженности Е₁ в области I проведем гаус­сову поверхность S₁ радиусом r₁ и воспользуемся теоремой Остроград­ского – Гаусса:

(так как суммарный заряд, находящийся внутри гауссовой поверхно­сти, равен нулю). Из соображений симметрии E_n=E₁=const. Следова­тельно, и Е₁ (напряженность поля в области I) во всех точ­ках, удовлетворяющих условию r₁<R₁, будет равна нулю.

2. В области II гауссову поверхность проведем радиусом r₂. В этом случае (диэлектрическую проницаемость среды будем считать равной единице (вакуум))

(так как внутри гауссовой поверхности находится только заряд q₁).

Так как E_n = E = const, то Е можно вынести за знак интеграла:

или ES₂ = q₁/ .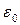

Обозначив напряженность Е для области II через Е₂, получим

Е₂ = q₁/(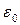 S₂),

где S₂ = 4πr₂² – площадь гауссовой поверхности. Тогда

(1)

3. В области III гауссова поверхность проводится радиусом r₃. Обозначим напряженность Е области III через Е₃ и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен q₁ + q_2. Тогда

Е₃ = (q₁+q₂)/4π 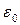r₃².

Заметив, что q₂<0, это выражение можно переписать в виде

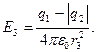(2)

Убедимся в том, что правая часть равенства (1) и (2)дает единицу на­пряженности:

Выразим все величины в единицах СИ (q₁ = 10^-9 Кл, q₂= - 0,5·10^-9 Кл, r₁=0,09 м, r₂=0,15 м, 1/(4πε₀)=9·10⁹ м/Ф) и произведем вычисления:

Построим график E(r). В области I(r₁<R₁) Е = 0. В области II (R₁ r<R₂) E₂(r) изменяется по закону 1/r². В точке r = R₁ напряжен­ность E₂(R₁) = q₁/(4π 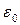R₁²)=2,25 кв/м. В точке r = R₂ (r стремится к R₂ слева) E₂(R₂) = q₁/(4π 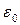R₂²) = 0,9 кВ/м. В области III (r>R₂) E₃(r) изменяется по закону 1/r², причем в точке r = R₂ (r стремится к R₂ справа) E₃(R₂) = (q₁ - |q₂|/(4π 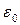R₂²) = 0,45 кВ/м. Таким образом, функ­ция E(r) в точках r = R₁ и r = R₂ терпит разрыв.

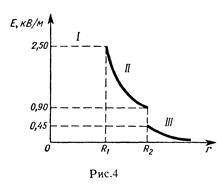
График зависимости E(r) представлен на рис. 4.

 

 

Пример 4. Электрическое поле создано длинным цилиндром радиусом R = 1 см, равномерно заряженным с линейной плотностью τ = 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии 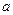₁ = 0,5 см и 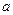₂ = 2 см от поверхности цилиндра, в средней его части.

Р е ш е н и е. Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и измене­нием потенциала: = -grad φ. Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде

E = - dφ/dr, или dφ = - Edr.

Интегрируя это выражение, найдем разность потенциалов двух точек, отстоящих на расстояниях r₁ и r₂ от оси цилиндра:

(1)

 

 

Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженно­сти поля можно воспользоваться формулой напряженности поля, соз­даваемого бесконечно длинным цилиндром:

E = τ/(2π 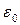r).

Подставив выражение Е в (1), получим

или

φ₁ – φ₂ = τ/(2π 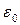)ln(r₂/r₁). (2)

Произведем подстановку, учитывая, что величины r₁ и r₂, входящие в формулу (2) в виде отношения, можно выразить в сантиметрах (r₁ = R + = 1,5 см r₂ = R + = 3 см):

φ₁ – φ₂ = 2 · 10 ^–8 · 1,8 · 10¹⁰ ln(3/1,5) = 3,6 · 10² · 2,3 ln2 В = 250 В.

 

Пример 5. Конденсатор емкостью С₁ = 3 мкФ был заряжен до разности потенциалов U₁ = 40 В. После отключения от источника тока конденсатор соединили с другим незаряженным конденсатором емко­стью С₂ = 5 мкФ. Какая энергия израсходуется на образование искры в момент присоединения второго конденсатора?

Р е ш е н и е. Энергия, израсходованная на образование искры,

= W₁ – W₂, (1)

где W₁ – энергия, которой обладает первый конденсатор до присоеди­нения к нему второго конденсатора; W₂ – энергия, которую имеет ба­тарея, составленная из двух конденсаторов.

Энергия заряженного конденсатора определяется по формуле

W = ½СU², (2)

где С – емкость конденсатора или батареи конденсаторов.

Выразив в формуле (1) энергии W₁ и W₂ по формуле (2) и при­няв во внимание, что общая емкость параллельно соединенных кон­денсаторов равна сумме емкостей отдельных конденсаторов, получим

= ½ C₁U₁² – ½(C₁ + C₂)U₂², (3)

где U₂ – разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что заряд после присоединения второго конденса­тора остался прежним, выразим разность потенциалов U₂ следующим образом:

Подставив выражение U₂ в (3), найдем

или

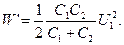
Произведем вычисления:

Пример 6 Потенциометр сопротивлением R = 100 Ом под­ключен к батарее с ЭДС e = 150 В и внутренним сопротивлением R_i = 50 Ом. Определить: 1) показание вольтметра между сопротивлением R_v = 500 Ом, соеди­ненного с одной из клемм потенциометра и подвижным контактом, установленным посе­редине потенциометра; 2) разность потен­циалов между теми же точками потенцио­метра при отключении вольтметра.

 

Рис. 5

 

Р е ш е н и е. 1. Показание вольт­метра, подключенного к точкам А и В (рис. 5), определим по формуле

U₁ = I₁R₁,

где R₁ – сопротивление параллельно соединенных вольтметра и поло­вины потенциометра; I₁ – суммарная сила тока в ветвях этого соедине­ния (она равна силе тока в неразветвленной части цепи).

Силу тока I₁ найдем по закону Ома для полной цепи:

I₁ = e /(R_e +R_i), (1)

где R_e – сопротивление внешней цепи. Это сопротивление есть сумма двух сопротивлений:

R_e = R/2 +R₁. (2)

Сопротивление R₁ найдем по формуле параллельного соедине­ния проводников откуда

Подставив в (1) выражение R_e по (2), найдем

В данном случае решение задачи в общем виде было бы гро­моздким. Поэтому удобно вычисление величин провести раздельно:

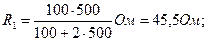
U₁ = 1,03·45·5 В = 46,9 В.

2. Разность потенциалов между точками А и В при отключен­ном вольтметре равна произведению силы тока I ₂ на половину сопро­тивления потенциометра:

U₂ = I₂ ·R/ 2, (3)

где I₂ – сила тока в цепи при отключенном вольтметре. Ее определим по формуле

I₂ = e /(R + R_i).

Подставив выражение I₂ в (3), найдем

U₂ = e / (R + R_i)·R/2.

Произведем вычисления:

Пример 7 Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Δt = 2 с по линейному закону от I₀ = 0 до I = 6 А (рис 6). Определить теплоту Q ₁, выделившуюся в этом проводнике за первую секунду, и Q₂ – за вторую, а также найти отношение q₁/q₂.

 

 

 

Рис. 6

Р е ш е н и е. Закон Джоуля – Ленца в виде Q = I²Rt справедлив для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон спра­ведлив для бесконечно малого интервала времени и записывается в виде

dQ = I²Rdt. (1)

Здесь сила тока I является некоторой функцией времени. В данном случае

I = kt, (2)

где k – коэффициент пропорциональности, характеризующий скорость изменения силы тока:

С учетом (2) формула (1) примет вид

dQ = k²Rt²dt. (3)

Для определения теплоты, выделившейся за конечный интер­вал времени Δ t, выражение (3) надо проинтегрировать в пределах от t ₁ до t ₂:

Произведем вычисления:

Q₁ = 1/3 · 3² · 20(1 – 0) Дж = 60 Дж;

Q₂ = 1/3 · 3² · 20(8 – 1) Дж = 420 Дж.

Следовательно,

Q₂ / Q₁ = 420 / 60 = 7,

т. е. за вторую секунду выделится теплоты в семь раз больше, чем за первую.

 

Пример 8 Пространство между пластинами плоского конден­сатора имеет объем V = 375 см³ и заполнено водородом, который час­тично ионизирован. Площадь пластин конденсатора S = 250 см². При каком напряжении U между пластинами конденсатора сила тока I, про­текающего через конденсатор, достигнет значения 2мкА, если концен­трация n ионов обоих знаков в газе равна 5,3 · 10⁷ см^–3. Принять под­вижность ионов b ₊= 5,4 · 10 ^–4 м² / (В · с), b _-=7,4 · 10^-4 м²/(В · с).

Р е ш е н и е. Напряжение U на пластинах конденсатора свя­зано с напряженностью Е электрического поля между пластинами и расстоянием d между ними соотношением

U = Ed. (1)

Напряженность поля может быть найдена из выражения плот­ности тока

j = qn(b₊ + b_-)E,

где q – заряд иона.

Отсюда

Расстояние d между пластинами, входящее в формулу (1), най­дем из соотношения

d = V/S.

Подставив выражения Е и d в (1), получим

(2)

 

 

Проверим, дает ли правая часть полученной расчетной фор­мулы единицу напряжения:

Подставим в формулу (2) значения величин и произведем вы­числения:

 

 

Таблица вариантов заданий

 

Вариант	Номера задач

 

1. Точечные заряды q₁=20 мкКл, q₂=-10 мкКл находятся на рас­стоянии d =5см друг от друга. Определить напряженность поля в точке, удаленной на r₁=3 см от первого и на r₂=4 см от второго за­ряда. Опре­делить также силу , действующую в этой точке на точечный заряд q= 1 мкКл.

2. Три одинаковых точечных заряда q₁=q₂=q₃=2 нКл находятся в вершинах равностороннего тре­угольника со сторонами а =10см. Опре­делить модуль и направление силы , действующей на один из заря­дов со стороны двух других.

3. Два положительных точечных заряда q и 9q закреплены на рас­стоянии d=100см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устой­чивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закреп­ленные заряды.

4. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол a. Ша­рики погружают в масло. Како­ва плотность r масла, если угол расхож­дения нитей при погружении в масло остается неизменным? Плотность материала шариков r₀=1,5×10³ кг/м³, диэлектрическая проницаемость масла e = 2,2.

5. Четыре одинаковых заряда q₁= q₂=q₃=q₄=40кНл закреплены в вершинах квадрата со стороной а =10см. Найти силу , действую­щую на один из этих зарядов со стороны трех остальных.

6. Точечные заряды q₁=30 мкКл и q₂=-20 мкКл находятся на рас­стоянии d =20 см друг от друга. Опре­делить напряженность электриче­ского поля в точке, удаленной от первого заряда на расстояние r₁ = 30 см, а от второго – на r₂ = 15 см.

7. В вершинах правильного треугольника со стороной а= 10 см находятся заряды q₁=10мкКл, q₂=20 мкКл и qз=30 мкКл. Определить силу , действую­щую на заряд q₁ со стороны двух других зарядов.

8. В вершинах квадрата находятся одинаковые заряды q₁=q₂=q₃=q₄= 8×10^-10 Кл. Какой отрица­тельный заряд q нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?

9. На расстоянии d=20 см находятся два точечных заряда: q₁=-50 нКл и q₂=100нКл. Определить силу , действующую на заряд q₃=-10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.

10. Расстояние d между двумя точечными зарядами q₁=2нКл и q₂=4нКл равно 60см. Определить точку, в которую нужно поместить третий заряд q₃ так, чтобы система зарядов находилась в равновесии. Определить заряд q₃ и его знак. Устойчивое или неустойчивое будет равновесие?

11. Тонкий стержень длиной l =20 см несет равномерно распреде­ленный заряд t=0,1 мкКл. Определить напряженность электриче­ского поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а=20 см от его конца.

12. По тонкому полукольцу радиуса R=10 см равномерно распре­делен заряд с линейной плотностью t = 1 мкКл/м. Определить напря­женность электрического поля, создаваемого распределенным заря­дом в точке О, совпадающей с центром кольца.

13. Тонкое кольцо несет распределенный заряд q=0,2 мкКл. Оп­ределить напряженность электрического поля, создаваемого распределенным зарядом в точке A, равноудаленной от всех точек кольца на расстояние г=20 см. Радиус кольца R=10см.

14. Треть тонкого кольца радиуса R=10см несет распределенный заряд q=50нКл. Определить напряженность электрического поля, создаваемого распре­деленным зарядом в точке О, совпадающей с цен­тром кольца.

15. Бесконечный тонкий стержень, ограниченный с одной сто­роны, несет равномерно распределенный заряд с линейной плотностью t=0,5 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а =20 см от его начала.

16. По тонкому кольцу радиусом R=20см равномерно распреде­лен с линейной плотностью t=0,2 мкКл/м заряд. Определить напря­женность электрического поля, создаваемого распределенным заря­дом в точке A, находящейся на оси кольца на расстоянии h=2R от его центра.

17. По тонкому полукольцу равномерно распределен заряд q=20 мкКл с линейной плотностью t=0,1 мкКл/м. Определить напря­женность электрического поля, создаваемого распределенным заря­дом в точке О, совпадающей с центром кольца.

18. Четверть тонкого кольца радиусом R=10см несет равномерно распределенный заряд q=0,05 мкКл. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке О, совпа­дающей с центром кольца.

19. По тонкому кольцу равномерно распределен заряд q=10 нКл с линейной плотностью t=0,01 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, рав­ное радиусу кольца.

20. Две трети тонкого кольца радиусом R=10см несут равномерно распределенный с линейной плотностью t=0,2 мкКл/м заряд. Опреде­лить напряженность электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

21. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями s₁ и s₂ (рис. 18). Требуется: 1) используя теорему Остроградского-Гаусса, найти зави­симость E(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять s₁=4s, s₂=s; 2) вычислить напряжен­ность Е в точке, удаленной от центра на расстояние r, и указать на­правление вектора .Принять s=30нКл/м², г= l,5R; 3) построить гра­фик E(r).

22. См. условие задачи 21. В п. 1 принять s₁=s, s₂=-s. В п. 2 при­нять s=0,1мкКл/м², r=3.

23. См. условие задачи 21. В п. 1 принять s₁=-4s, s₂=s. В п. 2 принять s=50 нКл/м², r=1,5R.

24. См. условие задачи 21. В п. 1 принять s₁=-2s, s₂=s. В п. 2 принять s=0,1мкКл/м², г==3R.

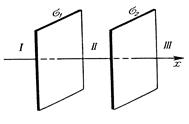
Рис. 18 Рис. 19

25. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями s₁ и s₂ (рис. 19). Требуется: 1) используя теорему Остроградского-Гаусса и принцип суперпози­ции электрических полей, найти выражение Е(х) напря­жен­ности электрического поля в трех областях: I, II и III.Принять s₁=2s, s₂=s; 2) вычислить напряженность Е по ля в точке, расположенной слева от плоскостей, и указать направление вектора ; 3) построить график Е(х)

26. См. условие задачи 25. В п. 1 принять s₁=-4s, s₂=2s. В п. 2 принять s=40 нКл/м² и точку расположить между плоскостями.

27. См. условие задачи 25. В п. 1 принять s₁=s, s₂=-2s. В п. 2 принять s=20 нКл/м² и точку располо­жить справа от плоскостей.

28. На двух коак­сиальных бесконечных цилиндрах радиусами R и 2R равномерно распре­делены заряды с поверх­ностными плот­ностями s₁ и s₂ (рис. 20). Требу­ется:

1) используя теорему Ост­роградского-Гаусса, найти за­висимость Е(r) напряженности электри­ческого поля от расстоя­ния для трех областей: I, II и III. Принять s₁=-2, s₂=s; 2) вычис­лить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направ­

 

Рис. 20

ление вектора . Принять s= 50нКл/м², r = 1,5R; 3) построить график E(r).

29. См. условие задачи 28. В п. 1 принять s₁=s, s₂=-s. В п. 2 при­нять s= 60нКл/м², r =3R.

30. См. условие задачи 28. В п. 1 принять s₁=-s, s₂=4s. В п. 2 принять s= 30нКл/м², r =4R.

31. Два точечных заряда q₁=6нКл и q₂=3нКлнаходятся на рас­стоянии d=60 см друг от друга. Какую работу необходимо совершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?

32. Электрическое поле создано заряженным проводящим шаром, потенциал j которого 300 В. Определить работу сил поля по переме­щению заряда q= 0,2мкКл из точки 1 в точку 2 (рис.21).

33. Электрическое поле создано зарядами q₁=2мкКл и q₂=-2мкКл, находящимися на расстояние а =10см друг от друга. Определить работу сил поля, совершаемую при перемещении заряда q=0,5мкКл из точки 1 в точку 2 (рис.22).

 

 

Рис. 21 Рис. 22

 

34. Две параллельные заряженные плоскости, поверхностные плотности заряда которых s₁=2мкКл/м² и s₂=-0,8мкКл/м², находятся на расстоянии d =0,6см друг от друга. Определить разность потенциалов U между плоскостями.

35. Диполь с электрическим моментом р = 100 пКл×м свободно установился в свободном электрическом поле напряженностью Е =200кВ/м. Определить работу внешних сил, которую необходимо совершить для поворота диполя на угол a=180°.

36. Четыре одинаковых капли ртути, заряженных до потенциала j=10В, сливаются в одну. Каков потен­циал j₁ образовавшейся капли?

37. Тонкий стержень согнут в кольцо радиусом R =10 см. Он рав­номерно заряжен с линейной плотностью заряда t=800нКл/м. Опреде­лить потенциал j в точке, расположенной на оси кольца на расстоянии h = 10см от его центра.

38. Поле образовано точечным диполем с электри­ческим момен­том р = 200пКл×м. Определить разность потенциалов U двух точек поля, расположенных симмет­рично относительно диполя на его оси на расстоянии r =40 см от центра диполя.

39. Электрическое поле образовано бесконечно длин­ной заряжен­ной нитью, линейная плотность заряда кото­рой t= 20пКл/м. Опреде­лить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r₁=8см и r₂= 12см.

40. Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда t=200пКл/м. Опреде­лить потенциал j поля в точке пересечения диагоналей.

41. Пылинка массой т =200мкг, несущая на себе заряд q=40нКл, влетела в электрическое поле в на­правлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость u = 10 м/с. Определить скорость u₀ пылинки до того, как она влетела в поле.

42. Электрон, обладавший кинетической энергией T = 10 эВ, вле­тел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потен­циалов U= 8В?

43. Найти отношение скоростей ионов Сu⁺⁺ и К⁺, прошедших одинаковую разность потенциалов.

44. Электрон с энергией Т = 400 эВ (в бесконечнос­ти) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R = 10 см. Определить минимальное рас­стояние а, на которое приблизится электрон к поверхности сферы, если заряд ее q = - 10 нКл.

45. Электрон, пройдя в плоском конденсаторе путь от одной пла­стины до другой, приобрел скорость u = 10⁵ м/с. Расстояние между пластинами d = 8 мм. Найти: 1) разность потенциалов U между пласти­нами; 2) поверхностную плотность зарядаs на пластинах.

46. Пылинка массой т = 5 нг, несущая на себе N = 10 электронов, прошла в вакууме ускоряющую разность потенциалов U = 1 MB. Ка­кова кинетическая энергия Т пылинки? Какую скорость u приобрела пылинка?

47. Какой минимальной скоростью u_min должен обладать протон, чтобы он мог достигнуть поверхности заряженного до потенциала j = 400 В металлического шара (рис.23)?

48. В однородное электрическое поле напряженностью Е = 200 В/м влетает (вдоль силовой линии) электрон со скоростью u₀=2 Мм/с. Определить расстояние l, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.

49. Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределенным зарядом (t = 10 нКл/м). Опреде­лить кинетическую энергию Т₂ электрона в точке 2, если в точке1его кинетическая энергия T₁= 200эВ (рис.24).

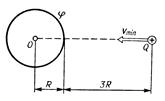
Рис. 23 Рис. 24

50. Электрон движется вдоль силовой линии однородного элек­трического поля. В некоторой точке поля с потенциалом j₁ = 100 В электрон имел скорость = 6 Мм/с. Определить потенциал j₂ точки поля, дойдя до которой электрон потеряет половину своей ско­рости.

51. Конденсаторы емкостью C₁ = 5 мкФ и С₂ = 10 мкФ заряжены до напряжений U₁ = 60 В и U₂ = 100 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обклад­ками, имеющими одноименные заряды.

52. Конденсатор емкостью C₁ = 10 мкФ заряжен до напряжения U = 10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный, конденса­тор ем­костью С₂ = 20 мкФ.

53. Конденсаторы емкостями C₁ = 2 мкФ, С₂ = 5 мкФ и С₃ = 10 мкФ соединены последовательно и находятся под напряжением U = 850 В. Определить на­пряжение и заряд на каждом из конденсато­ров.

54. Два конденсатора емкостями C₁ = 2 мкФ и С₂ = 5 мкФ заря­жены до напряжений U₁ = 100 В и U₂ = 150 В соответственно. Опреде­лить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.

55. Два одинаковых плоских воздушных конденсато­ра емкостью С=100 пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.

56. Два конденсатора емкостями C₁ = 5 мкФ и С₂ = 8 мкФ соеди­нены последовательно и присоединены к батарее с ЭДС e = 80 В. Оп­ределить заряды q₁ и q₂ конденсаторов и разности потенциалов U₁ и U₂. между их обкладками.

57. Плоский конденсатор состоит из двух круглых пластин радиу­сом R = 10см каждая. Расстояние между пластинами d = 2 мм. Конден­сатор присоединен к источ­нику напряжения U = 80 В. Определить заряд q и на­пряженность Е поля конденсатора в двух случаях: а) ди­электрик — воздух; б) диэлектрик — стекло.

58. Два металлических шарика радиусами R₁ = 5 см и R₂ = 10 см имеют заряды q₁ = 40 нКл и q₂ = -20 нКл соответственно. Найти энер­гию W, которая выделится при разряде, если шары соединить проводни­ком.

59. Пространство между пластинами плоского конденсатора за­полнено двумя слоями диэлектрика: стекла толщиной d₁ = 0,2 см и слоем парафина толщиной d₂ = 0,3 см. Разность потенциалов между обкладками U = 300 В. Определить напряженность E поля и падение потенциала в каждом из слоев.

60. Плоский конденсатор с площадью пластин S = 200 см² каждая заряжен до разности потенциалов U =2 кВ. Расстояние между пласти­нами d=2 см. Диэлектрик – стекло. Определить энергию W поля кон­денсатора и плотность энергии w поля.

61. Катушка и амперметр соединены последовательно и подклю­чены к источнику тока. К клеммам катушки присоединен вольтметр с сопротивлением r = 4 кОм. Амперметр показывает силу тока I = 0,3 А, вольтметр напряжение U = 120 В. Определить сопротивление Rка­тушки. Определить относительную погрешность e, которая будет до­пущена при измерении сопротивления, если пренебречь силой тока, текущего через вольтметр.

62. ЭДС батареи = 80 В, внутреннее сопротивление Ri = 5 Ом. Внешняя цепь потребляет мощность Р= 100 Вт. Определить силу тока I в цепи, напряжение U, под которым находится внешняя цепь, и ее со­противление R.

63. От батареи, ЭДС которой = 600 В, требуется передать энер­гию на расстояние l = 1 км. Потребляемая мощность Р = 5 кВт. Найти минимальные потери мощности в сети, если диаметр медных подво­дящих проводов d = 0,5 см.

64. При внешнем сопротивлении R₁ = 8 Ом силе тока в цепи I₁ = 0,8 А, при сопротивлении R₂ = 15 Ом сила тока I₂ = 0,5 А. Опреде­лить силу тока I_к.з. короткого замыкания источника ЭДС.

65. ЭДС батареи = 24 В. Наибольшая сила тока, которую может дать батарея, I_max = 10 А. Определите максимальную мощность P_max, которая может выделяться во внешней цепи.

66. Аккумулятор с ЭДС = 12 В заряжается от сети постоянного тока с напряжением U = 15 В. Определить напряжение на клеммах ак­кумулятора, если его внутреннее сопротивление Ri = 10 Ом.

67. От источника с напряжением U = 800 В необходимо передать потребителю мощность Р = 10 кВт на некоторое расстояние. Какое наибольшее сопротивление может иметь линия передачи, чтобы по­тери энергии в ней не превышали 10% от передаваемой мощности?

68. При включении электромотора в сеть с напряжением U = 220 В он потребляет ток I = 5 А. Определить мощность, потребляемую мото­ром, и его КПД, если сопротивление R обмотки мотора равно 6 Ом.

69. В сеть с напряжением U = 100 В подключили катушку с сопро­тивлением R₁ = 2 кОм и вольтметр, соединенные последовательно. По­казание вольтметра U₁ = 80 В. Когда катушку заменили другой, вольт­метр показал U₂ = 60 В. Определить сопротивление R₂ другой ка­тушки.

70. ЭДС батареи = 12 В. При силе тока I = 4 A КПД батареи h = 0,6. Определить внутреннее сопротивление Ri батареи.

71. За время t = 20 с при равномерно возраставшей силе тока от нуля до некоторого максимума в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Определить скорость на­растания силы тока, если сопротивление проводника R = 5 Ом.

72. Сила тока в проводнике изменяется со временем u закону I =I₀е^-at, где I₀ = 20 А, a=10²c^-1. Опреде­лить количество теплоты, выде­лившееся в проводнике за время t = 10^-2 с.

73. Сила тока в проводнике сопротивлением R = 10 Ом за время t = 50 с равномерно нарастает от I₁ = 5 А до I₂ = 10 А. Определить коли­чество теплотыQ,выделившееся за это время в проводнике.

74. В проводнике за время t = 10 с при равномерном возрастании силы тока от I₁ = 1 А до I₂ = 2 А выделилось количество теплоты Q = 5 кДж. Найти сопротивление R проводника.

75. Сила тока в проводнике изменяется со временем но закону I = I₀ sinwt. Найти заряд q, проходящий через поперечное сечение про­водника за время t, равное половине периода Т, если начальная сила тока = 10 А, циклическая частота w = 50pс^-l.

76. За время t = 10 с при равномерно возрастающей силе тока от нуля до некоторого максимума в проводнике выделилось количество теплоты Q = 40 кДж. Определить среднюю силу тока < I > в проводнике, если его сопро­тивление R = 25 Ом.

77. За время t = 8 с при равномерно возраставшей силе тока в проводнике сопротивлением R = 8 Ом выделилось количество теплоты Q = 500 Дж. Определить заряд q, проходящий в проводнике, если сила тока в на­чальный момент времени равна нулю.

78. Определить количество теплоты Q, выделившееся за время t = 10 с в проводнике сопротивлением R = 10 Ом, если сила тока в нем, равномерно уменьшаясь, изменилась от I₁ = 10 А до I₂ = 0.

79. Сила тока в цепи изменяется по закону I = I₀ sin wt. Опреде­лить количество теплоты, которое выделится в проводнике сопротив­лением R=10 Ом за время, равное четверти периода (от t₁ = 0 до t₂ = Т/4, где Т= 10 с).

80. Сила тока в цепи изменяется со временем по закону I = I₀ e^-at. Определить количество теплоты, которое выделится в проводнике со­противлением R = 20Oмза время, в течение которого ток уменьшится в е раз. Коэффициент a принять равным 2×10^-2c^-l.

81. Определить плотность тока, если за 2 с через проводник сече­нием 1,66 мм² прошло 2·10¹⁹ электронов.

82. По медному проводнику сечением 0,88 мм² течет ток 80 мА. Найти среднюю скорость упорядоченного движения электронов вдоль проводника, предполагая, что на каждый атом меди приходится один свободный электрон. Плотность меди ρ = 8,9 г/см³.

83. Лампа накаливания потребляет ток, равный 0,5 А. Темпера­тура накаливания вольфрамовой нити лампы диаметром 0,1 мм соот­ветствует 2200^о С; ток подводится медным проводником сечением 5 мм². Определить напряженность электрического поля в меди и вольфраме (для вольфрама ρ = 5,5·10^-8 Ом · м, α = 0,0045 1/^оС).

84. По медному проводнику сечением S = 0,17 мм² течет ток I = 0,15 А. Определить, какая сила действует на отдельные свободные электроны со стороны электрического поля.

85. Определить, какой ток создает электрон, вращающийся вокруг ядра в атоме водорода, если радиус его орбиты принять равным 5,3·10^{-9 см.}

86. Круглое кольцо из медной проволоки длиной 60 см и диамет­ром 0,1 мм включено так, как показано на рис.25. Найти сопротивление цепи. При какой длине меньшего участка АВ = x сопротивление цепи составит 0,2 Ом?

87. Ток 100 А течет по коническому медному проводнику, раз­меры которого показаны на рис.26. Определить плотность тока и на­пряженность электрического поля на торцах проводника.

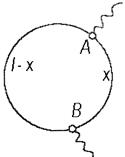
Рис. 25 Рис. 26

88. Определить общее сопротивление между точками А и В цепи, представленной на рис.27, если R₁=1Ом, R₂=3Ом, R₃=R₄=R₆=2Ом, R₅=4 Ом.

 

Рис. 27

89. Металлический диск вращается вокруг своей оси, перпенди­кулярной плоскости диски, с угловой скоростью ω = 100 с^-1. Радиус диска R = 10 см. Какая разность потенциалов должна возникнуть ме­жду центром и краем диска?

90. Определить подвижность ₊ одновалентных ионов азота, если плотность тока j = 5 · 10^-11 А/м², концентрация ионов n = 10⁹ м^-3, напряженность поля Е = 1000 В/м. Подвижность отрицательных ионов азота = 1,9 · 10^-4 м²/(В · с).

91. Газ находится в сосуде с плоскими параллельными электро­дами площадью S, расстояние между которыми d. Определить концен­трацию одновалентных ионов, если подвижность положительных ио­нов ₊, а отрицательных – _{_} Разность потенциалов между пласти­нами равна U, ток ионизации I.

92. Электроны, прошедшие ускоряющую разность потенциалов U=13,5В, вызывают ударную ионизацию водорода. Определить потен­циал ионизации водорода φ_i.

93. Отношение работ выхода электронов из платины и цезия A_Pt/A_Cs = 1,58. Определить отношение минимальных скоростей тепло­вого движения электронов, вылетающих из этих металлов.

94. Термопара железо – константан, постоянная которой α = 5,3 · 10^-5 В/К и сопротивление R = 15 Ом, замкнута на гальвано­метр. Один спай термопары находится в сосуде с тающим льдом, а второй помещен в среду, температура которой неизвестна. Определить эту температуру, если ток через гальванометр I = 0,2 мА, а внутреннее сопротивление гальванометра r = 150 Ом.

95. Средняя напряженность электрического поля Земли состав­ляет 130 В/м. Определить плотность тока проводимости в атмосфере, если в 1 м³ воздуха находится n =7 · 10⁸ м^-3 пар одновалентных ионов, обусловливающих проводимость.

96. Чему равно отношение числа свободных электронов в единице объема у висмута и сурьмы, если при нагревании одного из спаев на 100^оС возникает Э.Д.С. e = 0,011 В?

97. Найти отношение минимальных скоростей теплового движе­ния электронов, вылетающих из платины и цезия, если отношение ра­бот выхода A_Pt/A_Cs = 2,7.

98. Работа выхода электрона из металла А = 2,5 эВ. Определить скорость вылетающего из металла электрона, если он обладает энер­гией W = 10^-18 Дж.

99. Потенциал ионизации атома водорода U_i = 13,6 В. Определить температуру, при которой атомы водорода имеют среднюю кинетиче­скую энергию поступательного движения, достаточную для ионизации.

100. Какую скорость направленного движения имеют свободные электроны внутри медного проводника длиной 1 м, на концах которого поддерживается разность потенциалов 0,01 В?

Приложение

1.Основные физические постоянные (округленные значения)

 

Физическая постоянная	Обозначение	Значение
Нормальное ускорение свободного падения Гравитационная постоянная Постоянная Авогадро Молярная газовая постоянная Стандартный объем Постоянная Больцмана	g   G NA   R Vm k	9,81 м/с2   6,67×10-11 м3/(кг×с2) 6,02×1023 моль-1   8,31 Дж/(моль×К) 22,4×10-3 м3/моль 1,38×10-23 Дж/К

 

2. Некоторые астрономические величины

 

Наименование	Значение
Радиус Земли Масса Земли Радиус Солнца Масса Солнца Радиус Луны Масса Луны Расстояние от центра Земли до центра Солнца Расстояние от центра Земли до центра Луны	6,37×106 м 5,98×1024 кг 6,95×108 м 1,98×1030 кг 1,74×106 м 7,33×1022 кг   1,49×1011 м   3,84×108 м

 

3. Плотность твердых тел

 

Твердое тело	Плотность, кг/м3	Твердое тело	Плотность, кг/м3
Алюминий Барий Ванадий Висмут Железо Литий	2,70×103 3,50×103 6,02×103 9,80×103 7,88×103 0,53×103	Медь Никель Свинец Серебро Цезий Цинк	8,93×103 8,90×103 11,3×103 10,5×103 1,90×103 7,15×103

 

4. Плотность жидкостей

 

Жидкость	Плотность, кг/м3	Жидкость	Плотность, кг/м3
Вода (при 4о С) Глицерин Ртуть	1,00×103 1,26×103 13,6×103	Сероуглерод   Спирт	1,26×103   0,80×103

---

⇐ Предыдущая1234

Поделиться с друзьями:

---

Дата добавления: 2016-11-03; Мы поможем в написании ваших работ!; просмотров: 1071 | Нарушение авторских прав

---

Лучшие изречения:

© 2015-2024 lektsii.org - Контакты - Последнее добавление