Количество вещества тела (системы)
n = N/NA,
где N - число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему); NА - постоянная Авогадро
(NА = 6,02×1023моль-1).
Молярная масса вещества
M = m/n,
где m - масса однородного тела (системы); n - количество вещества этого тела.
Относительная молекулярная масса вещества
Mr = SniAr,i,
где ni - число атомов i-го химического элемента, входящих в состав молекулы данного вещества; Ar,i - относительная масса этого элемента. Относительные атомные массы приводятся в таблице Д.И.Менделева.
Связь молекулярной массы М с относительной молекулярной массой вещества
M = Mrk,
где k = 10-3 кг/моль.
Количество вещества смеси газов
n = n1 + n2 + … + nn = N1/NA + N2/NA + … + Nn/NA,
или
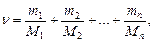
где ni, Ni, mi, Mi - соответственно количество вещества, число молекул, масса, молекулярная масса i-го компонента смеси.
Уравнение Менделеева-Клайперона (уравнение состояния идеального газа)
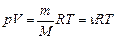
где m - масса газа, М - молекулярная масса газа, R - молекулярная газовая постоянная, n - количество вещества, Т - термодинамическая температура.
Опытные газовые законы, являющиеся частными случаями уравнения Менделеева-Клайперона для изопроцессов:
а) закон Бойля-Мариотта (изотермический процесс: T=const, m=const)
pV = const,
или для двух состояний газа
p1V1 = p2V2;
б) закон Гей-Люссака (изобарный процесс: p=const, m=const)
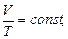
или для двух состояний
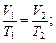
в) закон Шарля (изохорный процесс: V=const, m=const)
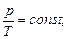
или для двух состояний
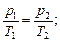
г) объединенный газовый закон (m=const)
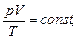 или
или 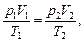
где p1,V1,T1 - давление, объем и температура газа в начальном состоянии; p2,V2,T2 - те же величины в конечном состоянии.
Закон Дальтона, определяющий давление смеси газов,
р = р1 + р2 + … + рn
где pi - парциальные давления компонентов смеси; n - число компонентов смеси.
Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.
Молекулярная масса смеси газов
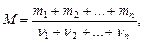
где mi - масса i-го компонента смеси; ni = mi/Mi - количество вещества i-го компонента смеси; n - число компонентов смеси.
Массовая доля i-го компонента смеси газа (в долях единицы или процентах)
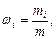
где m - масса смеси.
Концентрация молекул
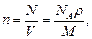
где N - число молекул, содержащихся в данной системе; r - плотность вещества; V - объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.
Основное уравнение кинетической теории газов
p = 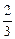 n áeпñ,
n áeпñ,
где áeпñ - средняя кинетическая энергия поступательного движения молекулы.
Средняя кинетическая энергия поступательного движения молекулы
áeпñ = 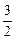 kT,
kT,
где k - постоянная Больцмана.
Средняя полная кинетическая энергия молекулы
áeiñ = 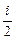 kT,
kT,
где i - число степеней свободы молекулы.
Зависимость давления газа от концентрации молекул и температуры
p = nkT.
Скорости молекул:
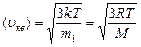 - средняя квадратичная;
- средняя квадратичная;
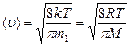 - средняя арифметическая;
- средняя арифметическая;
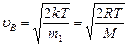 - наиболее вероятная,
- наиболее вероятная,
где mi - масса одной молекулы.
Относительная скорость молекулы
u = u/uB,
где u - скорость данной молекулы.
Удельные теплоемкости газа при постоянном объеме (сv) и постоянном давлении (cp)
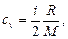
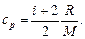
Связь между удельной с и молекулярной С теплоемкостями
с = С/М, С = сМ.
Уравнение Майера
Сp – Cv = R
Внутренняя энергия идеального газа
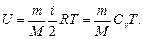
Первое начало термодинамики
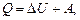
где Q - теплота, сообщенная системе (газу); DU - изменение внутренней энергии системы; А - работа, совершенная системой против внешних сил.
Работа расширения газа:
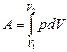 в общем случае;
в общем случае;
A = p(V2-V1) при изобарном процессе;
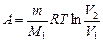 при изотермическом процессе;
при изотермическом процессе;
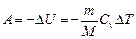 , или
, или 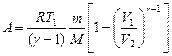
при адиабатном процессе, где g = сp/cv - показатель адиабаты.
Уравнения Пуассона, связывающие параметры идеального газа при адиабатном процессе:
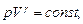
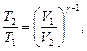
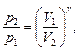
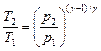
Термический КПД цикла
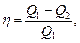
где Q1 - теплота, полученная рабочим телом от теплоотдатчика; Q2 - теплота, переданная рабочим телом теплоприемнику.
Термический КПД цикла Карно
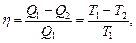
где T1 и T2 - термодинамические температуры теплоотдатчика и теплоприемника.
Коэффициент поверхностного натяжения
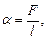 или
или 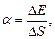
где F - сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости; DЕ - изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади DS поверхности этой пленки.
Формула Лапласа, выражающая давление р, создаваемое сферической поверхностью жидкости:
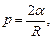
где R - радиус сферической поверхности.
Высота подъема жидкости в капиллярной трубке
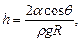
где q - краевой угол (q = 0 при полном смачивании стенок трубки жидкостью; q = p при полном несмачивании); R - радиус канала трубки; r - плотность жидкости; g - ускорение свободного падения.
Высота подъема жидкости между двумя близкими параллельными друг другу плоскостями
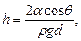
где d - расстояние между плоскостями.
Примеры решения задач
Пример 1. Определить молярную массу М смеси кислорода массой 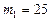 г и азота массой
г и азота массой 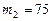 г.
г.
Решение. Молярная масса смеси М есть отношение массы смеси m к количеству вещества смеси 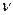 :
:
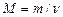 . (1)
. (1)
Масса смеси равна сумме масс компонентов смеси:
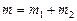 .
.
Количество вещества смеси равно сумме количеств вещества компонентов:
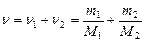 .
.
Подставив в формулу (1) выражения 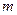 и
и 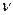 , получим
, получим
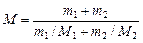 . (2)
. (2)
Найдем молярные массы кислорода 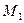 и азота
и азота 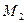 :
:
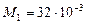 кг/моль;
кг/моль; 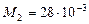 кг/моль.
кг/моль.
Подставим значения величин в (2) и произведем вычисления:
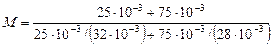 кг/моль =
кг/моль =
= 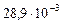 кг/моль.
кг/моль.
Пример 2. Найти среднюю кинетическую энергию 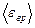 вращательного движения одной молекулы кислорода при температуре
вращательного движения одной молекулы кислорода при температуре 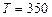 К, а также кинетическую энергию
К, а также кинетическую энергию 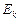 вращательного движения всех молекул кислорода массой
вращательного движения всех молекул кислорода массой 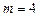 г.
г.
Решение. На каждую степень свободы молекулы газа приходится одинаковая средняя энергия 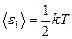 , где k – постоянная Больцмана; T – термодинамическая температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная) соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода
, где k – постоянная Больцмана; T – термодинамическая температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная) соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода
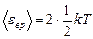 . (1)
. (1)
Кинетическая энергия вращательного движения всех молекул газа
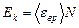 . (2)
. (2)
Число всех молекул газа
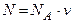 , (3)
, (3)
где 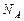 – постоянная Авогадро;
– постоянная Авогадро; 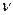 – количество вещества.
– количество вещества.
Если учесть, что количество вещества 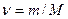 , где m – масса газа; М – молярная масса газа, то формула (3) примет вид
, где m – масса газа; М – молярная масса газа, то формула (3) примет вид
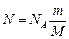 .
.
Подставив выражение N в формулу (2), получаем
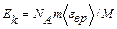 . (4)
. (4)
Произведем вычисления, учитывая, что для кислорода 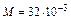 кг/моль:
кг/моль:
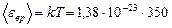 Дж
Дж 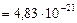 Дж;
Дж;
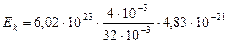 Дж
Дж 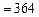 Дж.
Дж.
Пример 3. Вычислить удельные теплоемкости 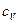 и
и 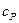 смеси неона и водорода, если массовые доли неона и водорода составляют
смеси неона и водорода, если массовые доли неона и водорода составляют 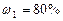 и
и 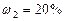 . Значения удельных теплоемкостей газов взять из справочника.
. Значения удельных теплоемкостей газов взять из справочника.
Решение. Удельную теплоемкость 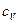 смеси при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания смеси на
смеси при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания смеси на 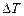 , выразим двумя способами:
, выразим двумя способами:
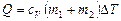 , (1)
, (1)
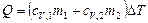 , (2)
, (2)
где 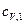 – удельная теплоемкость неона;
– удельная теплоемкость неона; 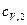 – удельная теплоемкость водорода.
– удельная теплоемкость водорода.
Приравняв правые части (1) и (2) и разделив обе части полученного равенства на 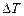 , получим
, получим 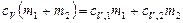 . Отсюда
. Отсюда
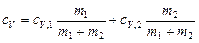 ,
,
или
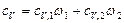 ,
,
где 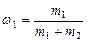 и
и 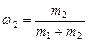 .
.
Рассуждая так же, получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:
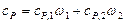 .
.
Произведем вычисления:
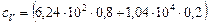
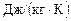 =
=
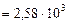
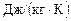
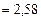
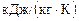 ;
;
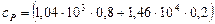
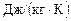 =
=
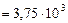
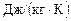
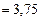
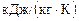 .
.
Пример 4. Кислород массой 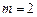 кг занимает объем
кг занимает объем
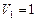
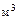 и находится под давлением
и находится под давлением 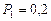 МПа. Газ был нагрет сначала при постоянном давлении до объема
МПа. Газ был нагрет сначала при постоянном давлении до объема 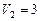 м3, а затем при постоянном объеме до давления
м3, а затем при постоянном объеме до давления 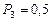 МПа. Найти изменение
МПа. Найти изменение 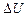 внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.
внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.
Решение. Изменение внутренней энергии газа
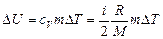 , (1)
, (1)
где i – число степеней свободы молекул газа (для двухатомных молекул кислорода i=5); 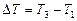 – разность температур газа в конечном (третьем) и начальном состояниях.
– разность температур газа в конечном (третьем) и начальном состояниях.
Начальную и конечную температуру газа найдем из уравнения Менделеева-Клапейрона 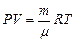 , откуда
, откуда
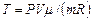 .
.
Работа расширения газа при постоянном давлении выражается формулой
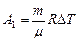 .
.
Работа газа, нагреваемого при постоянном объеме, равна нулю:
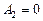 .
.
Следовательно, полная работа, совершаемая газом,
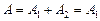 .
.
Согласно первому началу термодинамики, теплота Q, переданная газу, равна сумме изменения внутренней энергии 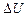 и работы A:
и работы A:
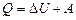 .
.
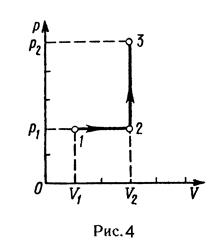 Произведем вычисления, учтя, что для кислорода
Произведем вычисления, учтя, что для кислорода
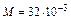 кг/моль:
кг/моль:
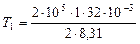 K =
K =
= 385 K;
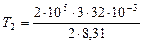 K =
K =
= 1155 K;
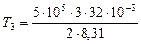 K =
K =
= 2887 K;
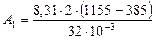 Дж
Дж 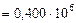 Дж
Дж 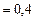 МДж;
МДж;
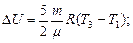
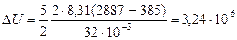 Дж = 3,24 МДж
Дж = 3,24 МДж
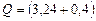 МДж
МДж 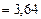 МДж.
МДж.
Пример 5. В цилиндре под поршнем находится водород массой 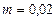 кг при температуре
кг при температуре 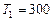 К. Водород сначала расширился адиабатно, увеличив свой объем в
К. Водород сначала расширился адиабатно, увеличив свой объем в 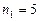 раз, а затем был сжат изотермически, причем объем газа уменьшился в
раз, а затем был сжат изотермически, причем объем газа уменьшился в 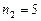 раз. Найти температуру в конце адиабатного расширения и работу, совершаемую газом при этих процессах.
раз. Найти температуру в конце адиабатного расширения и работу, совершаемую газом при этих процессах.
Решение. Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением
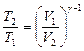 , или
, или 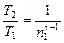 ,
,
где 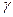 – отношение теплоемкостей газа при постоянном давлении и постоянном объеме;
– отношение теплоемкостей газа при постоянном давлении и постоянном объеме; 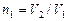 .
.
Отсюда получаем следующее выражение для конечной температуры:
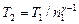 .
.
Работа 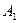 газа при адиабатном расширении может быть определена по формуле
газа при адиабатном расширении может быть определена по формуле
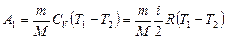 ,
,
где 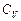 – молярная теплоемкость газа при постоянном объеме. Работа
– молярная теплоемкость газа при постоянном объеме. Работа 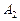 газа при изотермическом процессе может быть выражена в виде
газа при изотермическом процессе может быть выражена в виде
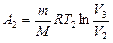 , или
, или 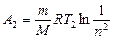 ,
,
где 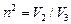 .
.
 Произведем вычисления, учитывая, что для водорода как двухатомного газа
Произведем вычисления, учитывая, что для водорода как двухатомного газа 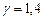 ,
, 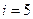 и
и 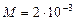 кг/моль:
кг/моль:
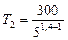 К
К 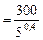 К.
К.
Так как 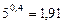 (находится логарифмированием), то
(находится логарифмированием), то
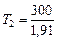 К
К 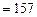 К;
К;
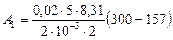 Дж
Дж 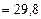 кДж;
кДж;
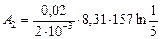 Дж
Дж 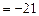 кДж.
кДж.
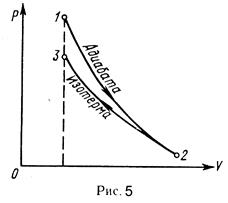
Знак минус показывает, что при сжатии работа газа совершается над газом внешними силами.
График процесса приведен на рис. 5.
Пример 6. Тепловая машина работает по обратимому циклу Карно. Температура теплоотдатчика 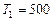 К. Определить термический КПД
К. Определить термический КПД 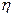 цикла и температуру
цикла и температуру 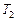 теплоприемника тепловой машины, если за счет каждого килоджоуля теплоты, полученной от теплоотдатчика, машина совершает работу
теплоприемника тепловой машины, если за счет каждого килоджоуля теплоты, полученной от теплоотдатчика, машина совершает работу 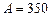 Дж.
Дж.
Решение. Термический КПД тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу. Термический КПД выражается формулой
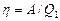 .
.
где 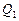 – теплота, полученная от теплоотдатчика; А – работа, совершенная рабочим телом тепловой машины.
– теплота, полученная от теплоотдатчика; А – работа, совершенная рабочим телом тепловой машины.
Зная КПД цикла, можно по формуле 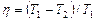 определить температуру охладителя
определить температуру охладителя 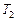 :
:
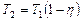 .
.
Произведем вычисления:
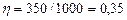 ;
; 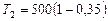 К
К 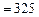 К.
К.
Пример 7. Найти добавочное давление внутри мыльного пузыря диаметром 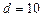 см. Какую работу нужно совершить, чтобы выдуть этот пузырь?
см. Какую работу нужно совершить, чтобы выдуть этот пузырь?
Решение. Пленка мыльного пузыря имеет две сферические поверхности: внешнюю и внутреннюю. Обе поверхности оказывают давление на воздух, заключенный внутри пузыря. Так как толщина пленки чрезвычайно мала, то диаметры обеих поверхностей практически одинаковы. Поэтому добавочное давление
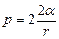 ,
,
где r – радиус пузыря. Так как 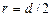 , то
, то
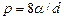 .
.
Работа, которую нужно совершить, чтобы, растягивая пленку, увеличить ее поверхность на 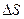 , выражается формулой
, выражается формулой
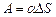 , или
, или 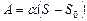 .
.
В данном случае S – общая площадь двух сферических поверхностей пленки мыльного пузыря; 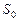 – общая площадь двух поверхностей плоской пленки, затягивавшей отверстие трубки до выдувания пузыря. Пренебрегая
– общая площадь двух поверхностей плоской пленки, затягивавшей отверстие трубки до выдувания пузыря. Пренебрегая 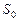 , получаем
, получаем
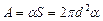 .
.
Произведем вычисления:
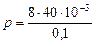 Па
Па 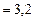 Па;
Па;
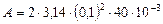 Дж
Дж 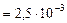 Дж
Дж 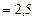 мДж.
мДж.
Таблица вариантов заданий
| Вариант | Номера задач | |||||||||
1. Тело брошено вертикально вверх с начальной скоростью V0=4 м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью V0 вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.
2. Материальная точка движется прямолинейно с ускорением а=5м/с2. Определить, на сколько путь, пройденный точкой в п-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять V0= 0.
3. Две автомашины движутся по дорогам, угол между которыми a=60°. Скорость автомашин V1=54 км/ч и V2=72км/ч. С какой скоростью V удаляются машины одна от другой?
4. Материальная точка движется прямолинейно с начальной скоростью V0=10 м/с и постоянным ускорением а=-5м/с2. Определить, во сколько раз путьΔs,пройденный материальной точкой, будет превышатьмодуль ее перемещения Δr спустя t=4c после начала отсчета времени.
5. Велосипедистехал из одного пункта в другой. Первую треть пути он проехал со скоростью V1=18 км/ч. Далее половину оставшегося времени он ехал со скоростью V2=22 км/ч, после чего до конечного пункта он шел пешком со скоростью V3=5км/ч. Определить среднюю скорость V велосипедиста.
6. Тело брошено под углом a = 30о к горизонту со скоростью vo = 30 м/с. Каковы будут нормальное an и тангенциальное at ускорения тела через время t = 1 с после начала движения.
7. Материальная точка движется по окружности с постоянной угловой скоростью w = p/6 рад/с. Во сколько раз путь Ds, пройденный точкой за время t = 4 с, будет больше модуля ее перемещения Dr? Принять, что в момент начала отсчета времени радиус-вектор r, задающий положение точки на окружности, относительно исходного положения был повернут на угол jо = p/3 рад.
8. Материальная точка движется в плоскости ху согласно уравнениям х = А1 + В1 t + С1 t2 и у = А2 + В2 t + С2 t2, где В1 = 7 м/с, С1 = - 2 м/с2, В2 = - 1 м/с, С2 = 0,2 м/с2. Найти модули скорости и ускорения точки в момент времени t = 5 с.
9. По краю равномерно вращающейся с угловой скоростью w = 1 рад/с платформы идет человек и обходит платформу за время
t = 9,9 с. Каково наибольшее ускорение а движения человека относительно Земли? Принять радиус платформы R = 2 м.
1 0. Точка движется по окружности радиусом R = 30 см с постоянным угловым ускорением e. Определить тангенциальное ускорение at точки, если известно, что за время t = 4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение
an = 2,7 м/с2.
1. При горизонтальном полете со скоростью V=250 м/с снаряд массой m=8кг разорвался на две части. Большая часть массой m1=6 кг получила скорость U1 =400м/c в направлении полета снаряда. Определить модуль и направление скорости U2 меньшей части снаряда.
12. С тележки, свободно движущейся по горизонтальному пути со скоростью V1=3 м/с, в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной U1 =4 м/с. Определить горизонтальную составляющую скорости U2x человека при прыжке относительно тележки. Масса тележки m1=210кг, масса человека m2=70 кг.
13. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом a=30° к линии горизонта. Определить скорость U2 отката платформы, если снаряд вылетает со скоростью U1 =480м/c. Масса платформы с орудием и снарядами m2=18т, масса снаряда m1=60 кг.
14. Человек массой m1=70 кг, бегущий со скоростью V1=9 км/ч, догоняет тележку массой m2=190кг, движущуюся со скоростью V2=3,6 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?
15. Конькобежец, стоя на коньках на льду, бросает камень массой m1=2,5 кг под углом a=30° к горизонту со скоростью V=10 м/с. Какова будет начальная скорость V0 движения конькобежца, если масса его m2=60 кг? Перемещением конькобежца во время броска пренебречь.
16. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m1=60 кг, масса доски m2=20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) V=1 м/с? Массой колес и трением пренебречь.
17. Снаряд, летевший со скоростью V = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью U1= 150 м/с. Определить скорость U2 большего осколка.
18. Две одинаковые лодки массами m = 200кг каждая (вместе с человеком и грузами, находящимися в лодках) движутся параллельными курсами навстречу друг другу с одинаковыми скоростями V=1 м/с. Когда лодки поравнялись, то с первой лодки на вторую и со второй на первую одновременно перебрасывают грузы массами m1=200 кг. Определить скорости U1 и U2 лодок после перебрасывания грузов.
19. На сколько переместится относительно берега лодка длиной l =3,5м и массой m1=200 кг, если стоящий на корме человек массой m2=80 кг переместится на нос лодки? Считать лодку расположенной перпендикулярно берегу.
20. Лодка длиной 1= 3 м и массой т= 120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами т1 =60 кг и т2 =90 кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?
21. В деревянный шар массой т1= 8 кг, подвешенный на нити длиной l =1,8 м, попадает горизонтально летящая пуля массой т2 = 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол a=3°? Размером шара пренебречь. Удар пули считать прямым, центральным.
22. По небольшому куску мягкого железа, лежащему на наковальне массой т1= 300 кг, ударяет молот массой т2 = 8 кг. Определить КПД h удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.
23. Шар массой m1 =1 кг движется со скоростью V1= 4 м/с и сталкивается с шаром массой т2=2 кг, движущимся навстречу ему со скоростью V2 = 3 м/с. Каковы скорости и1 и u2 шаров после удара? Удар считать абсолютно упругим, прямым, центральным.
24. Шар массой т1 =3 кг движется со скоростью V1 =2 м/с и сталкивается с покоящимся шаром массой т2 = 5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
25. Определить КПДh неупругого удара бойка массой т1 =0,5 т, падающего на сваю массой т2= 120 кг. Полезной считать энергию, затраченную на вбивание сваи.
26. Шар массой т1= 4 кг движется со скоростью V1= 5 м/с и сталкивается с шаром массой m2 =6 кг, который движется ему навстречу со скоростью V2= 2 м/с. Определить скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
27. Из ствола автоматического пистолета вылетела пуля массой m1 = 10 г со скоростью V = 300 м/с. Затвор пистолета массой m2 = 200 г прижимается к стволу пружиной, жесткость которой k =25 кН/м.На какое расстояние отойдет затвор послевыстрела? Считать, что пистолет жестко закреплен.
28. Шар массой т1 = 5 кг движется со скоростью V1 = 1 м/с и сталкивается с покоящимся шаром массой т2 = 2 кг. Определить скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
29. Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью V1 = 600 м/с, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью V2 = 580 м/с. С какой скоростью откатилось при этом орудие?
30. Шар массой т1 = 2 кг сталкивается с покоящимся шаром большей массы и при этом теряет 40% кинетической энергии. Определить массу т2 большего шара. Удар считать абсолютно упругим, прямым, центральным.
31. Определить работу растяжения двух соединенных последовательно пружин жесткостями k1 = 400 Н/м и k2 = 250 Н/м, если первая пружина при этом растянулась на D l = 2 см.
32. Из шахты глубиной h = 600 м поднимают клеть массой т1 = 3,0 т на канате, каждый метр которого имеет массу m = 1,5 кг. Какая работа A совершается при поднятии клети на поверхность Земли? Каков коэффициент полезного действия h подъемного устройства?
33. Пружина жесткостью k = 500 Н/м сжата силой F = 100 H. Определить работу A внешней силы, дополнительно сжимающей пружину еще на D l = 2 см.
34. Две пружины жесткостью k1 = 0,5 кН/м и k2 = 1 кН/м скреплены параллельно. Определить потенциальную энергию П данной системы при абсолютной деформации D l = 4 см.
35. Какую нужно совершить работу A, чтобы пружину жесткостью k = 800 Н/м, сжатую на х = 6 см, дополнительно сжать на Dx= 8 см?
36. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на D l = 3 мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты h = 8 см?
37. Из пружинного пистолета с пружиной жесткостью k = 150 Н/м был произведен выстрел пулей массой m = 8 г. Определить скорость V пули при вылете ее из пистолета, если пружина была сжата на Dx = 4 см.
38. Налетев на пружинный буфер, вагон массой m = 16 т, двигавшийся со скоростью V = 0,6м/с, остановился, сжав пружину на D l = 8 см. Найти общую жесткость k пружин буфера.
39. Цепь длиной l == 2 м лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает '/з l, то цепь соскальзывает со стола. Определить скорость V цепи в момент ее отрыва от стола.
40. Какая работа А должна быть совершена при поднятии с земли материалов для постройки цилиндрической дымоходной трубы высотой h = 40 м, наружным диаметром D = 3,0 м и внутренним диаметром d = 2,0 м? Плотность материала r принять равной 2,8×103 кг/м3.
41. Определить напряженность G гравитационного поля на высоте h = 1000 км над поверхностью Земли. Считать известными ускорение g свободного падения у поверхности Земли и ее радиус R.
42. Какая работа А будет совершена силами гравитационного поля при падении на Землю тела массой m = 2 кг:
1) с высоты h = 1000 км; 2) из бесконечности?
43. Из бесконечности на поверхность Земли падает метеорит массой m = 30 кг. Определить работу А, которая при этом будет совершена силами гравитационного поля Земли. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
44. С поверхности Земли вертикально вверх пущена ракета со скоростью v =5 км/с. На какую высоту она поднимется?
45. По круговой орбите вокруг Земли обращается спутник с периодом Т = 90 мин. Определить высоту спутника. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
46. На каком расстоянии от центра Земли находится точка, в которой напряженность суммарного гравитационного поля Земли и Луны равна нулю? Принять, что масса Земли в 81 раз больше массы Луны и что расстояние от центра Земли до центра Луны равно 60 радиусам Земли.
47. Спутник обращается вокруг Земли по круговой орбите на высоте h =520 км. Определить период обращения спутника. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
48. Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте h =1000 км. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
49. Какова масса Земли, если известно, что Луна в течение года совершает 13 обращений вокруг Земли и расстояние от Земли до Луны равно 3,84×108 м.
50. Во сколько раз средняя плотность земного вещества отличается от средней плотности лунного? Принять, что радиус Rз Земли в 390 раз больше радиуса Rл Луны и вес тела на Луне в 6 раз меньше веса тела на Земле.
51. Шарик массой т = 60 г, привязанный к концу нити длиной l1 =1,2 м, вращается с частотой п1=2с-1, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси до расстояния l2 =0,6 м. С какой частотой п2 будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.
52. По касательной к шкиву маховика в виде диска диаметром D = 75 см и массой т = 40 кг приложена сила F = 1 кН. Определить угловое ускорение e и частоту вращения п маховика через время t = 10 с после начала действия силы, если радиус r шкива равен 12 см. Силой трения пренебречь.
53. На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой т = 2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3 с приобрел угловую скорость w = 9 рад/с. 
54. Нить с привязанными к ее концам грузами массами т1 = 50 г и m 2 = 60 г перекинута через блок диаметром D =4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение e = 1,5 рад/с2. Трением и проскальзыванием нити по блоку пренебречь.
55. Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению j= At + Bt3, где А = 2 рад/с, В = 0,2 рад/с3. Определить вращающий момент М, действующий на стержень через время t = 2 с после начала вращения, если момент инерции стержня J =0,048 кг× м2
56. По горизонтальной плоскости катится диск со скоростью V = 8 м/с. Определить коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился, пройдя путь s = 18 м.
57. Определить момент силы М, который необходимо приложить к блоку, вращающемуся с частотой n = 12c-l, чтобы он остановился в течение времени Dt = 8 с. Диаметр блока D = 30 см. Массу блока т = 6 кг считать равномерно распределенной по ободу.
58. Блок, имеющий форму диска массой т = 0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами т1 = 0,3 кг и т2 = 0,7 кг. Определить силы натяжения Т1 и Т2 нити по обе стороны блока.
59. К краю стола прикреплен блок. Через блок перекинута невесомая и нерастяжимая нить, к концам которой прикреплены грузы. Один груз движется по поверхности стола, а другой - вдоль вертикали вниз. Определить коэффициент f трения между поверхностями груза и стола, если массы каждого груза и масса блока одинаковы и грузы движутся с ускорением а = 5,6 м/с2. Проскальзыванием нити по блоку и силой трения, действующей на блок, пренебречь.
60. К концам легкой и нерастяжимой нити, перекинутой через блок, подвешены грузы массами т1 = 0,2 кг и т2 = 0,3 кг. Во сколько раз отличаются силы, действующие на нить по обе стороны от блока, если масса блока m = 0,4 кг, а его ось движется вертикально вверх с ускорением а = 2 м/с2? Силами трения и проскальзывания нити по блоку пренебречь.
61. На скамье Жуковского сидит человек и держит на вытянутых руках гири массой т = 5 кг каждая. Расстояние от каждой гири до оси скамьи l 1 = 70 см. Скамья вращается с частотой п1 = 1с-1. Как изменится частота вращения скамьи и какую работу А произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l2 = 20 см? Момент инерции человека и скамьи (вместе) относительно оси J = 2,5 кг×м2.
62. На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью w1= 4 рад/с. С какой угловой скоростью w2 будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи J =5 кг×м2. Длина стержня l =1,8 м, масса m==6 кг. Считать, что центр масс стержня с человеком находится на оси платформы.
63. Платформа в виде диска диаметром D = 3 м и массой m1=180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью w1 будет вращаться эта платформа, если по ее краю пойдет человек массой m2 = 70 кг со скоростью V=1,8 м/с относительно платформы?
64. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол j повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную (на платформе) точку? Масса платформы m1 = 280 кг, масса человека m2 = 80 кг.
65. На скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью w1=25 рад/с. Ось колеса расположена вертикально и совпадает с осью скамьи Жуковского. С какой скоростью w2 станет вращаться скамья, если повернуть колесо вокруг горизонтальной оси на угол a=90°? Момент инерции человека и скамьи J равен 2,5 кг×м2, момент инерции колеса J0 = 0,5 кг×м2.
66. Однородный стержень длиной l =1,0 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой т=7 г, летящая перпендикулярно стержню и его оси. Определить массу М стержня, если в результате попадания пули он отклонится на угол a=60°. Принять скорость пули V=360 м/с.
67. На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой n1=8 мин--1, стоит человек массой m1=70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой п2=10 мин-1. Определить массу т2 платформы. Момент инерции человека рассчитывать как для материальной точки.
68. На краю неподвижной скамьи Жуковского диаметром D=0,8 м и массой m1=6 кг стоит человек массой m2=60 кг. С какой угловой скоростью w начнет вращаться скамья, если человек поймает летящий на него мяч массой m=0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии r=0,4 м от оси скамьи. Скорость мяча V=5 м/с.
69. Горизонтальная платформа массой m1=150 кг вращается вокруг вертикальной оси, проходящейчерезцентр платформы, с частотой n=8 мин--1. Человек массой т2= 70 кг стоит при этом на краю платформы. С какой угловой скоростью w начнет вращаться платформа, если человек перейдет от края платформы кеецентру? Считать платформу круглым, однородным диском, а человека — материальной точкой.
70. Однородный стержень длиной l =1,0 м и массой M1=0,7 кг подвешен на горизонтальной оси, проходящей через верхний конец стержня. В точку, отстоящую от оси на 2/3 l, абсолютно упруго ударяет пуля массой m = 5 г, летящая перпендикулярно стержню и его оси. После удара стержень отклонился на угол a=60°. Определить скорость пули.
71. На стержне длиной l =30 см укреплены два одинаковых грузика: один — в середине стержня, другой — на одном из его концов. Стержень с грузами колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т простых гармонических колебаний данного физического маятника. Массой стержня пренебречь.
72. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых х=A1 sinw t и y=A2 cosw t, где A1=8 см, А2=4 см, w =2 с-1. Написать уравнение траектории и построить ее. Показать направление движения точки.
73. Точка совершает простые гармонические колебания, уравнение которых x=Asinwt, где A=5 см, w =2c-1. В момент времени, когда точка обладала потенциальной энергией П=0,1 мДж, на нее действовала возвращающая сила F=5 мН. Найти этот момент времени t.
74. Определить частоту n простых гармонических колебаний диска радиусом R=20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.
75. Определить период Т простых гармонических колебаний диска радиусом R =40 см около горизонтальной оси, проходящей через образующую диска.
76. Определить период Т колебаний математического маятника, если его модуль максимального перемещения Dr = 18 см и максимальная скорость Vmax=16 см/с.
77. Материальная точка совершает простые гармонические колебания так, что в начальный момент времени смещение x0 = 4 см, а скорость V0=10 см/с. Определить амплитуду А и начальную фазу j0 колебаний, если их период Т=2 с.
78. Складываются два колебания одинакового направления и одинакового периода: х1=А1 sinw1t и x2 =A2sinw2(t+t), где А1 = А2 = 3см, w1 = w2 = pc-1, t=0,5 с. Определить амплитуду А и начальную фазу j0 результирующего колебания. Написать его уравнение. Построить векторую диаграмму для момента времени t=0.
79. На гладком горизонтальном столе лежит шар массой M=200 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью k= 500 Н/м. В шар попадает пуля массой m=10 г, летящая со скоростью V=300 м/с, и застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду А и период T колебаний шара.
80. Шарик массой m=60 г колеблется с периодом T=2 с. В начальный момент времени смещение шарика x0=4,0 см и он обладает энергией E=0,02 Дж. Записать уравнение простого гармонического колебания шарика и закон изменения возвращающей силы с течением времени.
81. Частица движется со скоростью u = с/3, где с — скорость света в вакууме. Какую долю энергии покоя составляет кинетическая энергия частицы?
82. Протон с кинетической энергией Т = 3 ГэВ при торможении потерял треть этой энергии. Определить, во сколько раз изменился релятивистский импульс a частицы.
83. При какой скорости b (в долях скорости света) релятивистская масса любой частицы вещества в п = 3 раза больше массы покоя?
84. Определить отношение релятивистского импульса р-электрона с кинетической энергией Т = 1,53 МэВ.к комптоновскому импульсу тос электрона.
85. Скорость электрона u = 0,8 с (где с — скорость света в вакууме). Зная энергию покоя электрона в мегаэлектрон-вольтах, определить в тех же единицах кинетическую энергию Т электрона.
86. Протон имеет импульс р = 469 МэВ/с*. Какую кинетическую энергию необходимо дополнительно сообщить протону, чтобы его релятивистский импульс возрос вдвое?
87. Во сколько раз релятивистская масса т электрона, обладающего кинетической энергией Т = 1,53 МэВ, больше массы покоя m0?
88. Какую скорость b (в долях скорости света) нужно сообщить частице, чтобы ее кинетическая энергия была равна удвоенной энергии покоя?
89. Релятивистский электрон имел импульс p1 = тос. Определить конечный импульс этого электрона (в единицах тос), если его энергия увеличилась в п == 2 раза.
90. Релятивистский протон обладал кинетической энергией, равной энергии покоя. Определить, во сколько раз возрастет его кинетическая энергия, если его импульс увеличится в п = 2 раза.
91. Определить количество вещества n и число N молекул кислорода массой m=0,5 кг.
92. Сколько атомов содержится в ртути: 1) количеством вещества n=0,2 моль; 2) массой m = 1 г?
93. Вода при температуре t =4°С занимает объем V = 1 см3. Определить количество вещества n и число N молекул воды.
94. Найти молярную массу М и массу от„ одной молекулы поваренной соли.
95. Определить массу тм одной молекулы углекислого газа.
96. Определить концентрацию п молекул кислорода, находящегося в сосуде вместимостью V=2л. Количество вещества n кислорода равно 0,2 моль.
97. Определить количество вещества n водорода, заполняющего сосуд объемом V =3 л, если концентрациямолекул газа в сосуде n=2×1018 м-3.
98. В баллоне вместимостью V=3л содержится кислород массой т= 10 г. Определить концентрацию п молекул газа.
99. Определить относительную молекулярную массу Mr: 1) воды; 2) углекислого газа; 3) поваренной соли.
100. Определить количество вещества n и число N молекул азота массой m=0,2кг.
101. В цилиндр длиной l =1,6м, заполненный воздухом при нормальном атмосферном давлении р0 , начали медленно вдвигать поршень площадью основания S= 200 см2. Определить силу F, действующую на поршень, если его остановить на расстоянии l1 =10см от дна цилиндра.
102. В баллоне находится газ при температуре Т1 =400 К. До какой температуры T 2 надо нагреть газ, чтобы его давление увеличилось в 1,5 раза?
103. Баллон вместимостью V =20л заполнен азотом при температуре T=400K. Когда часть газа израсходовали, давление в баллоне понизилось на Dr=200кПа. Определить массу m израсходованного газа. Процесс считать изотермическим.
104. В баллоне вместимостью V=15л находится аргон под давлением р1=600кПа и при температуре T1 = 300 К. Когда из баллона было взято некоторое количество газа, давление в баллоне понизилось до р2=400кПа, а температура установилась T2=260K. Определить массу m аргона, взятого из баллона.
105. Два сосуда одинакового объема содержат кислород. В одном сосуде давление р1=2МПа и температуре T1=800К, в другом р2=2,5МПа, T2=200К. Сосуд соединили трубкой и охладили находящийся в них кислород до температуры T=200К. Определить установившееся в сосудах давление р.
106. Вычислить плотность r азота, находящегося в баллоне под давлением р=2МПа и имеющего температуру T=400 К.
107. Определить относительную молекулярную массу Mr газа, если при температуре T=154К и давлении р=2,8МПа он имеет плотность r=6,1 кг/м3.
108. Найти плотность r азота при температуре T=400 К и давлении р=2 МПа.
109. В сосуде вместимостью V=40 л находится кислород при температуре T=300К. Когда часть газа израсходовали, давление в баллоне понизил




