Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси x
где f(t) - некоторая функция времени.
Проекция средней скорости на ось x
Средняя путевая скорость
где Ds - путь, пройденный точкой за интервал времени Dt. Путь Ds в отличие от разности координат Dx = x2-x1не может убывать и принимать отрицательные значения, т.е. Ds ³ 0.
Проекция мгновенной скорости на ось x
Проекция среднего ускорения на ось x
Проекция мгновенного ускорения на ось x
Кинематическое уравнение движения материальной точки по окружности
, r=R-const
Модуль угловой скорости
Модуль углового ускорения
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:
где 
-модуль линейной скорости; 
и 
- модули тангенциального и нормального ускорений; w - модуль угловой скорости; e - модуль углового ускорения; R -радиус окружности.
Модуль полного ускорения
или 
Угол между полным 
и нормальным ускорениями
Импульс материальной точки массой m, движущейся со скоростью ,
.
Второй закон Ньютона
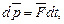
где 
- результирующая сила, действующая на материальную точку.
Силы, рассматриваемые в механике:
а) сила упругости
где 
-коэффициент упругости (в случае пружины - жесткость);
x - абсолютная деформация;
б) сила тяжести
в) сила гравитационного взаимодействия
где 
- гравитационная постоянная; m1 и m2 - массы взаимодействующих тел; r - расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряженность 
гравитационного поля:
г) сила трения (скольжения)
где f - коэффициент трения; N - сила нормального давления.
Закон сохранения импульса
или для двух тел (i=2)
,
где 
и 
- скорости тел в момент времени, принятый за начальный; 
и 
- скорости тех же тел в момент времени, принятый за конечный.
Кинетическая энергия тела, движущегося поступательно,
, или 
Потенциальная энергия:
а) упругодеформированной пружины
где - жесткость пружины; x - абсолютная деформация;
б) гравитационного взаимодействия
где 
- гравитационная постоянная; m1 и m2 - массы взаимодействующих тел; r - расстояние между ними (тела рассматриваются как материальные точки);
в) тела, находящегося в однородном поле силы тяжести,
где g - ускорение свободного падения; h - высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<R, где
R — радиус Земли).
Закон сохранения механической энергии
Работа А, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:
Примеры решения задач
Пример 1. Уравнение движения материальной точки вдоль оси имеет вид x = A + Bt + Ct3, где А = 2 м, В = 1 м/с, С = - 0,5 м/с3. Найти координату х, скорость 
и ускорение 
точки в момент времени t = 2с.
Решение. Координату xнайдем, подставив в уравнение движения числовые значения коэффициентов A, B и C и времени t:
x = (2 + 1×2 - 0,5×23)м = 0.
Мгновенная скорость относительно оси хесть первая производная от координаты по времени:
.
Ускорение точки найдем, взяв первую производную от скорости по времени:
В момент времени t = 2 с
= (1 - 3×0,5×22) м/c = - 5 м/c;
= 6(- 0,5) × 2 м/с2 = - 6 м/с2.
Пример 2. Тело вращается вокруг неподвижной оси по закону j = A + Bt + Ct2, где A= 10 рад, В = 20 рад/с, С = - 2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии г=0,1 м от оси вращения, для момента времени t =4 с.
Решение. Полное ускорение точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения , направленного по касательной к траектории, и нормального ускорения , направленного к центру кривизны траектории (рис.1):
Так как векторы и взаимно перпендикулярны, то модуль ускорения
Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами
где w - модуль угловой скорости тела; e - модуль его углового ускорения.
Подставляя выражения и в формулу (1), находим
. (2)
Угловую скорость w найдем, взяв первую производную угла поворота по времени:
В момент времени t = 4 с модуль угловой скорости
w = [20 + 2(-2)4] рад/с = 4 рад/с.
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:
= 2 C = - 4 рад/с2.
Подставляя значения w, e и r в формулу (2), получаем
м/с = 1,65 м/с2.
Пример 3. Шар массой m1, движущийся горизонтально с некоторой скоростью 
, столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?
Решение. Доля энергии, переданной первым шаром второму, выразится соотношением
(1)
где Т1 - кинетическая энергия первого шара до удара; u2 и Т2 - скорость и кинетическая энергия второго шара после удара.
Как видно из формулы (1), для определения e надо найти u2. Согласно условию задачи импульс системы двух шаров относительно горизонтального направления не изменяется и механическая энергия шаров в другие виды не переходит. Пользуясь этим, найдем:
(2)
(3)
Решим совместно уравнения (2) и (3):
Подставив это выражение u2 в формулу (1) и сократив на u1 и m1, получим
Из найденного соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров.
Пример 4. Через блок в виде сплошного диска, имеющего массу m= 80г (рис.2), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m1 = 100г и m2 = 200г. Определить ускорение, с которым будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь.
Решение: Рассмотрим силы, действующие на каждый груз и на блок в отдельности. На каждый груз действуют две силы: сила тяжести и сила упругости (сила натяжения нити). Направим ось х вертикально вниз и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось. Для первого груза
; (1)
для второго груза
(2)
Под действием моментов сил 
и 
относительно оси z перпендикулярной плоскости чертежа и направленной за чертеж, блок приобретает угловое ускорение e. Согласно основному уравнению динамики вращательного движения,
(3)
где 
- момент инерции блока (сплошного диска) относительно оси z.
Согласно третьему закону Ньютона, с учетом невесомости нити 
и 
. Воспользовавшись этим подставим в уравнение (3) вместо 
и выражения 
и 
, получив их предварительно из уравнений (1) и (2):
После сокращения на 
и перегруппировки членов найдем
(4)
Формула (4) позволяет массы m1, m2 и m выразить в граммах, как они даны в условии задачи, а ускорение - в единицах СИ. После подстановки числовых значений в формулу (4) получим
Пример 5. Ракета установлена на поверхности Земли для запуска в вертикальном направлении. При какой минимальной скорости u1, сообщенной ракете при запуске, она удалится от поверхности на расстояние, равное радиусу Земли (R=6,37×106 м)? Всеми силами, кроме силы гравитационного взаимодействия ракеты и Земли,пренебречь.
Решение. Со стороны Земли на ракету действует сила тяжести, являющаяся потенциальной силой. При неработающем двигателе под действием потенциальной силы механическая энергия ракеты изменяться не будет. Следовательно,
Т1 + П1 = Т2 + П2, (1)
где Т1, П1 и Т2, П2 - кинетическая и потенциальная энергии ракеты после выключения двигателя в начальном (у поверхности Земли) и конечном (на расстоянии, равном радиусу Земли) состояниях.
Согласно определению кинетической энергии,
Потенциальная энергия ракеты в начальном состоянии
По мере удаления ракеты от поверхности Земли ее потенциальная энергия возрастает, а кинетическая - убывает. В конечном состоянии кинетическая энергия Т2 станет равной нулю, а потенциальная - достигнет максимального значения:
Подставляя выражения Т1, П1, Т2 и П2 в (1), получаем
откуда
Заметив, что GM/R2=g (g - ускорение свободного падения у поверхности Земли), перепишем эту формулу в виде
что совпадает с выражением для первой космической скорости.
Произведем вычисления:
м/с = 7,9 км/с.
