Таблиця 8.1
ЗІМКНЕННЯ ДИНАМІЧНИХ РЯДІВ
| Місяці | Обсяг витрат, т | Зімкнений ряд | ||
| Старий порядок реєстрації | Новий порядок реєстрації | відносних величин, % | абсолютних величин, т | |
| Січень | — | 44,0 | ||
| Лютий | — | 49,5 | ||
| Березень | — | 52,8 | ||
| Квітень | 55,0 | |||
| Травень | — | 58,0 | ||
| Червень | — | 60,0 |
Другий спосіб ґрунтується на співвідношенні квітневих рівнів: 55: 50 = 1,1. Помноживши рівні першого ряду на цей коефіцієнт, дістанемо єдиний зімкнений (порівнянний) ряд динаміки за весь період (остання графа таблиці).
8.2. Характеристики інтенсивності динаміки
Швидкість та інтенсивність розвитку різних суспільних явищ значно варіюють, що позначається на структурі відповідних динамічних рядів. Для оцінювання зазначених властивостей динаміки статистика використовує низку взаємозв’язаних характеристик. Серед них: абсолютний приріст, відносний приріст, темп зростання, інші.
Розрахунок характеристик динаміки ґрунтується на порівнянні рівнів ряду. При порівнянні певної множини послідовних рівнів база порівняння може бути постійною чи змінною. За постійну базу вибирається або початковий рівень ряду, або рівень, який уважається вихідним для розвитку явища, що вивчається. Характеристики динаміки, обчислені відносно постійної бази, називаються базисними. Якщо кожний рівень ряду  порівнюється з попереднім
порівнюється з попереднім  , характеристики динаміки називаються ланцюговими. Схематично варіанти порівняння ілюструє рис. 8.1.
, характеристики динаміки називаються ланцюговими. Схематично варіанти порівняння ілюструє рис. 8.1.

Рис. 8.1. Схеми порівняння при обчисленні ланцюгових
і базисних характеристик динаміки
Абсолютний приріст  характеризує абсолютний розмір збільшення (чи зменшення) рівня ряду
характеризує абсолютний розмір збільшення (чи зменшення) рівня ряду  за певний часовий інтервал і обчислюється як різниця рівнів ряду:
за певний часовий інтервал і обчислюється як різниця рівнів ряду:
базисний приріст  ;
;
ланцюговий приріст 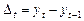 .
.
Знак «+», «–» свідчить про напрям динаміки.
Темп зростання 
 показує, у скільки разів рівень
показує, у скільки разів рівень  більший (менший) від рівня, узятого за базу порівняння. Він являє собою кратне відношення рівнів:
більший (менший) від рівня, узятого за базу порівняння. Він являє собою кратне відношення рівнів:
базисний темп  ,
,
ланцюговий темп  .
.
При збільшенні рівня  , при зменшенні —
, при зменшенні —  . Темпи зростання виражаються як у коефіцієнтах, так і в процентах.
. Темпи зростання виражаються як у коефіцієнтах, так і в процентах.
Ланцюгові  і
і  відображують відповідно абсолютну і відносну швидкість динаміки. Вони взаємозв’язані. Якщо подати
відображують відповідно абсолютну і відносну швидкість динаміки. Вони взаємозв’язані. Якщо подати  +
+  , то
, то
 .
.
Отже, при стабільній абсолютній швидкості темпи зростання зменшуватимуться. Стабільні темпи зростання можливі за умови прискорення абсолютної швидкості.
Величину  називають відносним прискоренням або темпомприросту і позначають символом
називають відносним прискоренням або темпомприросту і позначають символом 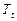 . Вона функціонально пов’язана з темпом зростання, але на відміну від останнього завжди виражається в процентах:
. Вона функціонально пов’язана з темпом зростання, але на відміну від останнього завжди виражається в процентах:
 .
.
Отже, темп приросту показує, на скільки процентів рівень  більший (менший) від бази порівняння.
більший (менший) від бази порівняння.
Співвідношенням абсолютного приросту і темпу приросту визначається абсолютне значення 1% приросту. Нескладні алгебраїчні перетворення цього відношення показують, що воно становить соту частину рівня, узятого за базу порівняння:
 .
.
У табл. 8.2 наведені всі розглянуті характеристики динаміки на прикладі виробництва синтетичних волокон за 3 роки. Очевидно, що ланцюгові й базисні характеристики динаміки взаємопов’язані:
а) сума ланцюгових абсолютних приростів дорівнює кінцевому базисному:
 .
.
У нашому прикладі: 12 + 9 = 21 тис. т;
б) добуток ланцюгових темпів зростання дорівнює кінцевому базисному:
 .
.
У нашому прикладі: 1,072 · 1,051 = 1,127 або 186: 165 = 1,127.
Щодо темпів приросту, то вони не мають таких властивостей, як абсолютні прирости чи темпи зростання. Ланцюгові й базисні темпи приросту співвідносяться через темпи зростання.
Таблиця 8.2
АБСОЛЮТНІ ТА ВІДНОСНІ ХАРАКТЕРИСТИКИ ДИНАМІКИ
| Порядковий номер року, t | Обсяг виробництва уt, тис.т | Абсолютний приріст, тис.т | Темп зростання | Темп приросту,% | Абсолютне значення 1% приросту, т | ||||
| ланцюговий | базисний | ланцюговий | базисний | ланцюговий | базисний | ланцюговий | базисний | ||
| — | — | — | 1,0 | — | — | — | — | ||
| 1,072 | 1,072 | 7,2 | 7,2 | 1,65 | 1,65 | ||||
| 1,051 | 1,127 | 5,1 | 12,7 | 1,77 | 1,65 |
Якщо швидкість розвитку в межах періоду, що вивчається, неоднакова, порівнянням однойменних характеристик швидкості вимірюється прискореннячи уповільнення динаміки. На базі абсолютних приростів оцінюються абсолютне та відносне прискорення. Абсолютне — це різниця між абсолютними приростами: 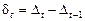 . Прискорення характеризується додатною величиною
. Прискорення характеризується додатною величиною  > 0, уповільнення — від’ємною
> 0, уповільнення — від’ємною  .
.
Обчислимо характеристики прискорення на прикладі табл. 8.2:  = 9 – 12 = – 3 тис. т. Знак «мінус» свідчить про уповільнення динаміки. Темп уповільнення абсолютної швидкості обчислюється порівнянням абсолютних приростів: 9: 12 = 0,75.
= 9 – 12 = – 3 тис. т. Знак «мінус» свідчить про уповільнення динаміки. Темп уповільнення абсолютної швидкості обчислюється порівнянням абсолютних приростів: 9: 12 = 0,75.
Порівняння темпів зростання дає коефіцієнт прискорення(уповільнення) відносної швидкості розвитку. Для наочності та зручності їх тлумачення дільником є більший за значенням темп зростання. У нашому прикладі коефіцієнт уповільнення відносної швидкості динаміки 1,072: 1,051 = 1,02.
У статистичному аналізі порівнюється також інтенсивність динаміки в різних рядах. Відношення темпів зростання  називають коефіцієнтом випередження. За допомогою останнього порівнюють відносну швидкість динамічних рядів однакового змісту по різних об’єктах (регіони, країни тощо) або різного змісту по одному об’єкту. Наприклад, за 3 роки фондоозброєність праці в одній галузі зросла на 50%, в іншій — на 25%. Коефіцієнт випередження темпу зростання фондоозброєності праці в першій галузі порівняно з другою становить 1,50: 1,25 = 1,20.
називають коефіцієнтом випередження. За допомогою останнього порівнюють відносну швидкість динамічних рядів однакового змісту по різних об’єктах (регіони, країни тощо) або різного змісту по одному об’єкту. Наприклад, за 3 роки фондоозброєність праці в одній галузі зросла на 50%, в іншій — на 25%. Коефіцієнт випередження темпу зростання фондоозброєності праці в першій галузі порівняно з другою становить 1,50: 1,25 = 1,20.
Можна порівняти динаміку фондоозброєності та продуктивності праці в кожній галузі. Якщо фондоозброєність зросла на 25%, а продуктивність праці — на 37,5%, то коефіцієнт випередження зростання продуктивності праці становить 1,375: 1,250 = 1,10.
Щодо темпів приросту, то співвідношення їх використовують лише для взаємозв’язаних показників х і у. Таке співвідношення називають емпіричним коефіцієнтом еластичності  ; він показує, на скільки процентів змінюється у зі зміною х на 1%. Наприклад, ціна на товар А зросла на 2%, а попит зменшився на 4%. Цінова еластичність попиту на цей товар
; він показує, на скільки процентів змінюється у зі зміною х на 1%. Наприклад, ціна на товар А зросла на 2%, а попит зменшився на 4%. Цінова еластичність попиту на цей товар  , тобто зі зростанням цін на 1% попит на товар зменшується на 2%.
, тобто зі зростанням цін на 1% попит на товар зменшується на 2%.
8.3. Середня абсолютна та відносна швидкість розвитку
З плином часу змінюються, варіюють рівні динамічних рядів і обчислені на їх основі абсолютні прирости та темпи зростання. Постає потреба узагальнення притаманних динамічному ряду властивостей, визначення типових характеристик розвитку. Такими характеристиками є середні величини. Зауважимо, що динамічна середня буде типовою характеристикою лише за умови однорідності ряду, коли причинний комплекс формування закономірностей розвитку більш-менш стабільний.
Середні рівні використовують насамперед для узагальнення коливних рядів. Наприклад, при аналізі динаміки сільськогосподарського виробництва оперують не річними, а більш сталими середньорічними показниками за певні періоди. Середні рівні необхідні також для забезпечення порівнянності чисельника і знаменника при побудові динамічних рядів похідних показників. Наприклад, виробництво продукції на одного працюючого. Обсяг продукції — інтервальний показник, а кількість працюючих — моментний. Щоб забезпечити порівнянність цих показників, слід обчислити середньорічну кількість працюючих.
Метод обчислення середнього рівня динамічного ряду залежить від статистичної структури показника. В інтервальному ряді абсолютних величин, рівні якого динамічно адитивні, використовується середня арифметична проста:
 ,
,
де n — число рівнів ряду.
У моментному ряді, за припущення про рівномірну зміну показника між датами, середня розраховується як півсума значень на початок і кінець періоду:
 .
.
Якщо в моментному ряді n > 2 і між суміжнимі датами однакові інтервали, розрахунок виконується за формулою середньоїхронологічної:
 .
.
Обґрунтування та розрахунок такої середньої наведено в підрозд. 4.4.
У моментних рядах з різними інтервалами між датами розраховується середня арифметична зважена:
 ,
,
де  — інтервал часу між датами, m — кількість інтервалів.
— інтервал часу між датами, m — кількість інтервалів.
Середній абсолютний приріст (абсолютна швидкість динаміки) обчислюється діленням загального приросту за весь період на довжину цього періоду у відповідних одиницях часу (рік, квартал, місяць тощо):
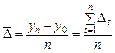 .
.
Наприклад, 1996 року автомобільним транспортом переве-
зено 2072 тис. т вантажів, 1999 року — 2126 тис. т. Середьо-
річний приріст цього показника за 1997 — 1999 рр. становить  = (2126 – 2072): 3 = 18 тис. т.
= (2126 – 2072): 3 = 18 тис. т.
При обчисленні середнього темпу зростання враховується правило складних процентів, за якими змінюється відносна швидкість динаміки (нагромаджується приріст на приріст). Тому середній темп зростання обчислюється за формулою середньої геометричної з ланцюгових темпів зростання:
 ,
,
де n — кількість темпів зростання за однакові інтервали часу.
Наприклад, за останні 3 роки невпинно зростали тарифи на
автоперевезення. Темпи зростання становили: 1997 р. — 1,03; 1998 р. — 1,08; 1999 р. — 1,05. Середьорічний темп зростання
 або 105,3 %.
або 105,3 %.
Урахувавши взаємозв’язок ланцюгових і базисних темпів зростання, формулу середньої геометричної можна записати так:
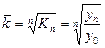 .
.
Скажімо, вартість споживчого кошика за три роки зросла на 12,5%. Середньорічний темп зростання становить

Тобто щороку споживчий кошик дорожчав у середньому на 4%. Розрахунок можна виконувати за допомогою логарифмів:  або
або  . Наприклад, прямі іноземні інвестиції в галузь 1996 року становили 172 млн дол. США, 1999 року — 313,7. Десяткові логарифми, відповідно, 2,2355 і 2,4965. Звідси
. Наприклад, прямі іноземні інвестиції в галузь 1996 року становили 172 млн дол. США, 1999 року — 313,7. Десяткові логарифми, відповідно, 2,2355 і 2,4965. Звідси  Потенціювання дає
Потенціювання дає 
Отже, середній темп зростання можна обчислити на основі:
· ланцюгових темпів зростання kt;
· кінцевого (за весь період) темпу зростання Kn;
· кінцевого yn і базисного y 0 рівнів ряду.
При інтерпретації середньої абсолютної чи відносної швидкості динаміки необхідно вказувати часовий інтервал, до якого належать середні, та часову одиницю вимірювання (рік, квартал, місяць, доба тощо).
8.3. Середня абсолютна та відносна швидкість розвитку
З плином часу змінюються, варіюють рівні динамічних рядів і обчислені на їх основі абсолютні прирости та темпи зростання. Постає потреба узагальнення притаманних динамічному ряду властивостей, визначення типових характеристик розвитку. Такими характеристиками є середні величини. Зауважимо, що динамічна середня буде типовою характеристикою лише за умови однорідності ряду, коли причинний комплекс формування закономірностей розвитку більш-менш стабільний.
Середні рівні використовують насамперед для узагальнення коливних рядів. Наприклад, при аналізі динаміки сільськогосподарського виробництва оперують не річними, а більш сталими середньорічними показниками за певні періоди. Середні рівні необхідні також для забезпечення порівнянності чисельника і знаменника при побудові динамічних рядів похідних показників. Наприклад, виробництво продукції на одного працюючого. Обсяг продукції — інтервальний показник, а кількість працюючих — моментний. Щоб забезпечити порівнянність цих показників, слід обчислити середньорічну кількість працюючих.
Метод обчислення середнього рівня динамічного ряду залежить від статистичної структури показника. В інтервальному ряді абсолютних величин, рівні якого динамічно адитивні, використовується середня арифметична проста:
 ,
,
де n — число рівнів ряду.
У моментному ряді, за припущення про рівномірну зміну показника між датами, середня розраховується як півсума значень на початок і кінець періоду:
 .
.
Якщо в моментному ряді n > 2 і між суміжнимі датами однакові інтервали, розрахунок виконується за формулою середньоїхронологічної:
 .
.
Обґрунтування та розрахунок такої середньої наведено в підрозд. 4.4.
У моментних рядах з різними інтервалами між датами розраховується середня арифметична зважена:
 ,
,
де  — інтервал часу між датами, m — кількість інтервалів.
— інтервал часу між датами, m — кількість інтервалів.
Середній абсолютний приріст (абсолютна швидкість динаміки) обчислюється діленням загального приросту за весь період на довжину цього періоду у відповідних одиницях часу (рік, квартал, місяць тощо):
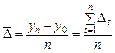 .
.
Наприклад, 1996 року автомобільним транспортом переве-
зено 2072 тис. т вантажів, 1999 року — 2126 тис. т. Середьо-
річний приріст цього показника за 1997 — 1999 рр. становить  = (2126 – 2072): 3 = 18 тис. т.
= (2126 – 2072): 3 = 18 тис. т.
При обчисленні середнього темпу зростання враховується правило складних процентів, за якими змінюється відносна швидкість динаміки (нагромаджується приріст на приріст). Тому середній темп зростання обчислюється за формулою середньої геометричної з ланцюгових темпів зростання:
 ,
,
де n — кількість темпів зростання за однакові інтервали часу.
Наприклад, за останні 3 роки невпинно зростали тарифи на
автоперевезення. Темпи зростання становили: 1997 р. — 1,03; 1998 р. — 1,08; 1999 р. — 1,05. Середьорічний темп зростання
 або 105,3 %.
або 105,3 %.
Урахувавши взаємозв’язок ланцюгових і базисних темпів зростання, формулу середньої геометричної можна записати так:
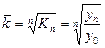 .
.
Скажімо, вартість споживчого кошика за три роки зросла на 12,5%. Середньорічний темп зростання становить

Тобто щороку споживчий кошик дорожчав у середньому на 4%. Розрахунок можна виконувати за допомогою логарифмів:  або
або  . Наприклад, прямі іноземні інвестиції в галузь 1996 року становили 172 млн дол. США, 1999 року — 313,7. Десяткові логарифми, відповідно, 2,2355 і 2,4965. Звідси
. Наприклад, прямі іноземні інвестиції в галузь 1996 року становили 172 млн дол. США, 1999 року — 313,7. Десяткові логарифми, відповідно, 2,2355 і 2,4965. Звідси  Потенціювання дає
Потенціювання дає 
Отже, середній темп зростання можна обчислити на основі:
· ланцюгових темпів зростання kt;
· кінцевого (за весь період) темпу зростання Kn;
· кінцевого yn і базисного y 0 рівнів ряду.
При інтерпретації середньої абсолютної чи відносної швидкості динаміки необхідно вказувати часовий інтервал, до якого належать середні, та часову одиницю вимірювання (рік, квартал, місяць, доба тощо).
8.4. Характеристика основної
тенденції розвитку
Будь-який динамічний ряд у межах періоду з більш-менш стабільними умовами розвитку виявляє певну закономірність зміни рівнів — загальну тенденцію. Одним рядам притаманна тенденція до зростання, іншим — до зниження рівнів. Зростання чи зниження рівнів динамічного ряду, у свою чергу, відбувається по-різному: рівномірно, прискорено чи уповільнено. Нерідко ряди динаміки через коливання рівнів не виявляють чітко вираженої тенденції.
Щоб виявити й схарактеризувати основну тенденцію, застосовують різні способи згладжування та аналітичного вирівнювання динамічних рядів.
Суть згладжування полягає в укрупненні інтервалів часу та заміні первинного ряду рядом середніх по інтервалах. У середніх взаємоврівноважуються коливання рівнів первинного ряду, внаслідок чого тенденція розвитку вирізняється чіткіше.
Залежно від схеми формування інтервалів розрізняють ступінчасті та ковзні (плинні) середні. Ряди цих середніх схематично зображено на рис. 8.2 для інтервалу m = 3. Очевидно, що ковзна середня більш гнучка і може краще відбити особливості тенденції.

Рис. 8.2. Схеми утворення інтервалів згладжування
динамічних рядів
При розрахунку ковзних середніх кожний наступний інтервал утворюється на основі попереднього заміною одного рівня. Оскільки середня 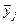 належить до середини інтервалу, то доцільно формувати інтервали з непарного числа рівнів первинного ряду. У разі парного числа рівнів необхідна додаткова процедура центрування (усереднення кожної пари значень
належить до середини інтервалу, то доцільно формувати інтервали з непарного числа рівнів первинного ряду. У разі парного числа рівнів необхідна додаткова процедура центрування (усереднення кожної пари значень 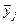 ).
).
Ряд ковзних середніх коротший за первинний на (m – 1) рівнів, що потребує уважного ставлення до вибору ширини інтервалу m. Якщо первинному ряду динаміки притаманна певна періодичність коливань, то інтервал згладжування має бути рівним або кратним періоду коливань.
Порядок згладжування методом ковзної середньої розглянемо на прикладі динамічного ряду врожайності зернових у регіоні (табл. 8.3). Ширина інтервалу згладжування m = 3. Первинний ряд складається із семи рівнів, ряд ковзних середніх — з п’яти, тобто на два рівні коротший (7 – 3 + 1).
Таблиця 8.3
РОЗРАХУНОК КОВЗНИХ СЕРЕДНІХ УРОЖАЙНОСТІ ЗЕРНОВИХ
| Порядковий номер року |  , ц/га , ц/га
| Ковзна середня 
| Розрахунок 
|
| 23,8 | — | — | |
| 19,1 | 21,6 | (23,8 + 19,1 + 21,9): 3 = 21,6 | |
| 21,9 | 22,2 | 21,6 + (25,6 – 23,8): 3 = 22,2 | |
| 25,6 | 24,0 | 22,2 + (24,5 – 19,1): 3 = 24,0 | |
| 24,5 | 26,2 | 24,0 + (28,5 – 21,9): 3 = 26,2 | |
| 28,5 | 26,9 | 26,2 + (27,7 – 25,6): 3 = 26,9 | |
| 27,7 | — | — |
Перше значення ковзної середньої обчислюється як арифметична проста, кожне наступне можна визначити на основі попередньої середньої та коригуючого доданка. Наприклад:
 (ц/га);
(ц/га);
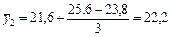 (ц/га);
(ц/га);
 (ц/га) і т. д.
(ц/га) і т. д.
У згладженому ряді трирічних ковзних середніх усунено первинні коливання врожайності й чітко виявляється систематичне підвищення її рівня.
Метод ковзних середніх застосовують також для попередньої обробки дуже коливних динамічних рядів; можливе подвійне згладжування.
При аналітичному вирівнюванні динамічного ряду фактичні значення yt замінюються обчисленими на основі певної функції Y = f (t), яку називають трендовим рівнянням (t — змінна часу, Y — теоретичний рівень ряду).
Вибір типу функції ґрунтується на теоретичному аналізі суті явища, яке вивчається, і характері його динаміки. Зазвичай перевага надається функціям, параметри яких мають чіткий економічний зміст і вимірюють абсолютну чи відносну швидкість розвитку. Суттєвою підмогою при виборі функцій є аналіз ланцюгових характеристик інтенсивності динаміки. Якщо ланцюгові абсолютні прирости відносно стабільні, не мають чіткої тенденції до зростання чи зменшення, вирівнювання ряду виконується на основі лінійної функції:  . Якщо ж відносно стабільними є ланцюгові темпи приросту, то найбільш адекватною такому характеру динаміки є експонента
. Якщо ж відносно стабільними є ланцюгові темпи приросту, то найбільш адекватною такому характеру динаміки є експонента  . У зазначених функціях t — порядковий номер періоду (дати), а — рівень ряду при t = 0. Параметр b характеризує швидкість динаміки: середню абсолютну в лінійній функції і середню відносну — в експоненті. Коли характеристики швидкості розвитку зростають (чи зменшуються), використовуються інші функції (парабола 2-го степеня, модифікована експонента тощо).
. У зазначених функціях t — порядковий номер періоду (дати), а — рівень ряду при t = 0. Параметр b характеризує швидкість динаміки: середню абсолютну в лінійній функції і середню відносну — в експоненті. Коли характеристики швидкості розвитку зростають (чи зменшуються), використовуються інші функції (парабола 2-го степеня, модифікована експонента тощо).
Параметри трендових рівнянь визначають методом найменших квадратів. Згідно з умовою мінімізації суми квадратів відхилень фактичних рівнів ряду  від теоретичних
від теоретичних  параметри визначаються розв’язуванням системи нормальних рівнянь. Для лінійної функції вона записується так:
параметри визначаються розв’язуванням системи нормальних рівнянь. Для лінійної функції вона записується так:
 ,
,
 .
.
Система рівнянь спрощується, якщо початок відліку часу (t = 0) перенести в середину динамічного ряду. Тоді значення t, розміщені вище середини, будуть від’ємними, а нижче — додатними. При непарнoму числі членів ряду (наприклад, n = 5) змінній t надаються значення з інтервалом одиниця: –2, –1, 0, 1, 2; при парному: –2,5, –1,5, –0,5, 0,5, 1,5, 2,5. В обох випадках 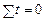 , а система рівнянь набирає вигляду
, а система рівнянь набирає вигляду
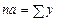 ,
,
 .
.
Отже, 
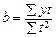 . Значення
. Значення  можна визначити за формулами:
можна визначити за формулами:
для непарного числа членів ряду
 ;
;
для парного числа членів ряду
 .
.
Порядок обчислення параметрів лінійної функції розгляне-
мо на прикладі динамічного ряду видобутку нафти в регіоні (табл. 8.4).
Таблиця 8.4
ДИНАМІКА ВИДОБУТКУ НАФТИ
| Рік |  , млн т , млн т
| Δ t | Змінна часу t | yt t |  = 74,5 + 3,8 t = 74,5 + 3,8 t
|
| 63,5 | — | –3 | –190,5 | 63,1 | |
| 66,8 | 3,3 | –2 | –133,6 | 66,9 | |
| 71,0 | 4,2 | –1 | –71,0 | 70,7 | |
| 74,3 | 3,3 | 74,5 | |||
| 76,9 | 2,6 | 76,9 | 78,3 | ||
| 82,2 | 5,3 | 164,4 | 82,1 | ||
| 86,8 | 4,6 | 260,4 | 85,9 | ||
| Разом | 521,5 | ´ | 106,6 | 521,5 |
Ланцюгові абсолютні прирости динамічного ряду практично стабільні, тому тенденцію можна описати лінійною функцією. Оскільки довжина ряду n = 7, то Σ t ² = 7 (7² – 1): 12 = 28. Параметри трендового рівняння становлять:
a = Σ yt: n = 521,5: 7 =74,5;
b = Σ yt t: Σ t ² = 106,6: 28 = 3,8.
Лінійний тренд має вигляд  = 74,5 + 3,8 t, тобто середній рівень видобутку нафти становить 74,5 млн т, середньорічний приріст видобутку — 3,8 млн т.
= 74,5 + 3,8 t, тобто середній рівень видобутку нафти становить 74,5 млн т, середньорічний приріст видобутку — 3,8 млн т.
В останній графі таблиці для кожного року наведено теоретичні рівні  , тобто очікувані рівні видобутку нафти в t -му році, зумовлені дією основних чинників розвитку галузі: для 1993 р.
, тобто очікувані рівні видобутку нафти в t -му році, зумовлені дією основних чинників розвитку галузі: для 1993 р.  = 74,5 + 3,8 (–3) = 63,1 млн т, для 1994 р.
= 74,5 + 3,8 (–3) = 63,1 млн т, для 1994 р.  = 74,5 + 3,8 (–2) =
= 74,5 + 3,8 (–2) =
= 66,9 млн т і т. д.
Суми фактичних рівнів  і розрахованих за лінійним трендом теоретичних рівнів
і розрахованих за лінійним трендом теоретичних рівнів  однакові:
однакові:  =
=  = 521,5 млн т.
= 521,5 млн т.
Продовження виявленої тенденції за межі ряду динаміки називають екстраполяцією тренду. Це один із методів статистичного прогнозування, передумовою використання якого є незмінність причинного комплексу, що формує тенденцію. Прогнозний, очікуваний рівень  залежить від бази прогнозування та періоду упередження v. Так, припускаючи, що умови, в яких формувалась тенденція видобутку нафти, найближчим часом не зміняться, визначимо прогноз на 2001 рік. Базою прогнозування є теоретичний рівень 1999 р., період упередження v = 2. Очікуваний в 2001 р. видобуток нафти досягне 93,5 млн т:
залежить від бази прогнозування та періоду упередження v. Так, припускаючи, що умови, в яких формувалась тенденція видобутку нафти, найближчим часом не зміняться, визначимо прогноз на 2001 рік. Базою прогнозування є теоретичний рівень 1999 р., період упередження v = 2. Очікуваний в 2001 р. видобуток нафти досягне 93,5 млн т:
 = 85,9 + 3,8 · 2 = 93,5.
= 85,9 + 3,8 · 2 = 93,5.
Метод екстраполяції дає точковий прогноз. На практиці, як правило, визначають довірчі межі прогнозного рівня  , де
, де 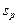 — стандартна похибка прогнозу, t -квантиль розподілу Стьюдента (див. підрозд. 6.2).
— стандартна похибка прогнозу, t -квантиль розподілу Стьюдента (див. підрозд. 6.2).
8.5. Оцінка коливань та сталості динаміки
Фактичні рівні динамічних рядів під впливом різного роду чинників варіюють, відхиляючись від основної тенденції розвитку. В одних рядах коливання мають систематичний, закономірний характер, повторюються через певні інтервали часу, в інших — не мають такого характеру і тому називаються випадковими. У конкретному ряду можуть поєднуватися систематичні та випадкові коливання.
Найпростішою оцінкою систематичних коливань є коефіцієнтинерівномірності, які обчислюються відношенням максимального і мінімального рівнів динамічного ряду до середнього. Чим більша нерівномірність процесу, тим більша різниця між цими двома коефіцієнтами.
Наприклад, споживання питної води за добу становить 7200 м3, у середньому за годину 7200: 24 = 300 м3. Найбільший рівень споживання води в період від 20 до 21 години — 381 м3, найменший — у період від 2 до 3 год — 165 м3.
Коефіцієнти нерівномірності такі:
K max = 381: 300 = 1,27;
K min = 165: 300 = 0,55.
Амплітуда коливань у розмірі 72 пункти [100 (1,27 – 0,55)] свідчить про істотну нерівномірність споживання води протягом доби.
Окремим соціально-економічним процесам притаманні внутрішньорічні, сезонні піднесення і спади. Наприклад, виробництво й переробка сільськогосподарської продукції, нерівномірне завантаження транспорту, коливання попиту на товари тощо. Сезонні коливання виявляються і аналізуються на основі рядів щомісячних або щоквартальних даних.
Характер сезонних коливань описується «сезонною хвилею», яку утворюють індекси сезонності. У динамічних рядах, які не виявляють чіткої тенденції розвитку, індекси сезонності є відношенням фактичних місячних (квартальних) рівнів  до середньомісячного (середньоквартального) за рік
до середньомісячного (середньоквартального) за рік  , %:
, %:
 .
.

|
| Рис. 8.3. Сезонна хвиля споживання електроенергії |
Порядок обчислення сезонної хвилі розглянемо на прикладі споживання електроенергії комунальним господарством регіону (табл. 8.5). Середньомісячний обсяг споживання  = 1848:: 12 = 154 млн квт × год. Індекси сезонності коливаються від 121,4% у грудні [(187: 154)100] до 80,5% у липні [124: 154)100]. Амп-
= 1848:: 12 = 154 млн квт × год. Індекси сезонності коливаються від 121,4% у грудні [(187: 154)100] до 80,5% у липні [124: 154)100]. Амп-
літуда сезонних коливань ста-
новить Rt = 121,4 – 80,5 =
= 40,9 п. п. Характер сезонної хвилі схематично ілюструє рис. 8.3.
Оскільки сезонні коливання з року в рік не лишаються незмінними, виявити сталу сезонну хвилю можна за допомогою середніх індексів сезонності за кілька років:
 ,
,
де n — число років.
Таблиця 8.5
ЩОМІСЯЧНА ДИНАМІКА СПОЖИВАННЯ ЕЛЕКТРОЕНЕРГІЇ
| Місяць року | Спожито електроенергії, уt, млн квт · год | Індекс сезонності Іс, % | Іс – 100 | (Іс – 100)2 |
| Січень | 111,7 | 11,7 | 136,89 | |
| Лютий | 104,5 | 4,5 | 20,25 | |
| Березень | 102,6 | 2,6 | 6,76 | |
| Квітень | 98,0 | –2,0 | 4,00 | |
| Травень | 95,5 | –4,6 | 20,25 | |
| Червень | 84,4 | –15,6 | 243,36 | |
| Липень | 80,5 | –19,5 | 380,25 | |
| Серпень | 94,9 | –5,1 | 26,01 | |
| Вересень | 96.8 | –3,2 | 10,24 | |
| Жовтень | 100,6 | 0,6 | 0,36 | |
| Листопад | 109,1 | 9,1 | 82,81 | |
| Грудень | 121,4 | 21,4 | 457,96 | |
| Разом | 1389,14 |
Для порівняння інтенсивності сезонних коливань різних явищ чи одного й того самого явища в різні роки використовуються узагальнюючі характеристики варіації індексів сезонності:
середнє лінійне відхилення  ;
;
або середнє квадратичне відхилення 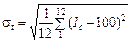 .
.
У динамічному ряду споживання електроенергії (табл. 8.5) середнє квадратичне відхилення:
 п. п.
п. п.
Якщо спостерігається тенденція розвитку, попередньо проводиться згладжування чи вирівнювання динамічного ряду, визначаються теоретичні рівні для кожного місяця (кварталу) року, а індекс сезонності обчислюється як відношення фактичних рівнів ряду  до теоретичних
до теоретичних  , тобто
, тобто  .
.
Розрахунок сезонної хвилі за наявності тенденції подано в табл. 8.6 на прикладі щоквартальної динаміки продажу безалкогольних напоїв (млн дкл). Тенденція ряду описується рівнянням Yt = 48,2 +
+ 1,445 t, де t змінюється в межах від t 1= –5,5 до tn = +5,5.
Таблиця 8.6
ТРЕНД І СЕЗОННІ КОЛИВАННЯ ПРОДАЖУ БЕЗАЛКОГОЛЬНИХ НАПОЇВ
| Рік | Квартал | Млн дкл, yt | Тренд Yt | Індекс сезонності | Тренд, скоригований на сезоність, Yt  = = 
|
| 24,4 | 40,3 | 0,606 | 27,7 | ||
| 52,6 | 41,7 | 1,262 | 51,0 | ||
| 60,4 | 43,1 | 1,401 | 59,0 | ||
| 34,0 | 44,6 | 0,763 | 32,1 | ||
| 32,7 | 46,0 | 0,711 | 31,6 | ||
| 56,2 | 47,5 | 1,184 | 58,0 | ||
| 67,3 | 48,9 | 1,377 | 66,9 | ||
| 36,2 | 50,4 | 0,719 | 36,1 | ||
| 37,8 | 51,8 | 0,730 | 35,6 | ||
| 65,3 | 53,3 | 1,225 | 65,1 | ||
| 73,1 | 54,7 | 1,337 | 74,9 | ||
| 38,4 | 56,1 | 0,689 | 40,4 | ||
| Разом | ´ | 578,4 | 578,4 | 578,4 |
Середньозважені індекси сезонності (для яких ваги — середньорічні обсяги продажу) становлять:
Для першого кварталу

Аналогічно розраховані індекси для другого кварталу  для третього
для третього  для четвертого
для четвертого  .
.
Скоригований на сезонність тренд наведено в останній графі табл. 8.6. Для першого кварталу 1997 р.
 .
.
Відхилення фактичних рівнів yt від скоригованих трендів  зумовлено дією випадкових причин.
зумовлено дією випадкових причин.
Абсолютною мірою випадкових коливань є середнєквадратичне відхилення  , яке обчислюється на основі залишкової дисперсії:
, яке обчислюється на основі залишкової дисперсії:
 .
.
За даними табл. 8.7 залишкова дисперсія продажу безалкогольних напоїв становить

звідки  .
.
Таблиця 8.7






