В некоторых случаях формулы для вычисления коэффициентов Фурье могут быть упрощены. Это имеет место для четных и нечетных функций.
Приведем несколько очевидных свойств четных и нечетных функций.
I. Произведение четной функции на четную или нечетной на нечетную есть функция четная.
II. Произведение четной функции на нечетную есть функция нечетная
III. Если 
– четная функция, то 
.
IV. Если – нечетная функция, то 
.
Допустим, что нужно разложить в ряд Фурье четную функцию 
.
Так как 
– функция четная, а 
– функция нечетная, то произведение 
будет функцией четной, а 
– функцией нечетной (свойства I и II). На основании свойств III и IV получим
,
,
.
Соответственно этому ряд Фурье для четной функции будет иметь вид
.
Если требуется разложить в ряд Фурье нечетную функцию, то вследствие свойств I и II произведение будет функцией нечетной, а – функцией четной. Поэтому
,
.
Ряд Фурье для нечетной функции будет иметь вид
.
Таким образом, четная функция разлагается в ряд только по косинусам, а нечетная функция – только по синусам кратных дуг.
§3. Разложение в ряд Фурье 
периодических функций
Пусть функция , удовлетворяющая условиям Дирихле, имеет период 
, т.е. 
.
В случае функции , имеющей период , коэффициенты Эйлера-Фурье вычисляются по формулам:
, 
, 
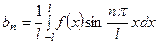(2)
(8)
В точках разрыва функции и в концах 
интервала сумма ряда Фурье определяется аналогично тому, как это имеет место при разложении в интервале 
.
В случае разложения функции в ряд Фурье в произвольном интервале 
длины пределы интегрирования в формулах (2) следует заменить соответственно на 
и 
.
Пример. Разложить в ряд Фурье периодическую функцию с периодом 2, заданную на отрезке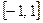 
уравнением 
.
Решение. Рассматриваемая функция является четной. Ее график – дуга параболы, заключенная между точками 
и 
.
|
Так как – четная функция, то и 
будет четной функцией. Здесь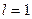 
, поэтому
,
.
Интегрируя дважды по частям, получим.
1) 
.
.
2) 
.
.
Так как рассматриваемая функция – четная, то . Следовательно,
.●
Если функция задана на отрезке 
, то для разложения в ряд Фурье достаточно доопределить ее на отрезке 
произвольным способом, а затем разложить в ряд Фурье, считая ее заданной на сегменте 
. Наиболее целесообразно функцию доопределить так, чтобы ее значения в точках сегмента находилась из условия 
или 
. В первом случае функция на сегменте будет четной, а во втором – нечетной. При этом часто говорят, что функция в интервале разложена в ряд Фурье по синусам или косинусам кратных дуг.
Пример. Разложить функцию 
, заданную на полупериоде 
, в ряд по синусам.
Решение. Для разложения функции в ряд по синусам надо ее продолжить на интервал 
нечетным образом, затем продолжить полученную функцию периодически на всю числовую ось.
; 
Здесь надо принять l = 1 и = 1. Тогда
Итак, ряд Фурье для данной функции имеет вид
.●
