Рассмотрим общий случай знакопеременного ряда
,
где числа 
могут быть как положительными, так и отрицательными.
Для таких рядов имеет место общий достаточный признак сходимости знакопеременного ряда.
Теорема. Если для знакопеременного ряда
Ряд, составленный из абсолютных величин его членов
Сходится, то данный знакопеременный ряд также сходится.
Пример 1. Исследуем на сходимость знакопеременный ряд
Решение. Рассмотрим ряд, составленный из абсолютных величин данного ряда
Этот ряд сходится, как обобщенный гармонический ряд с показателем 
. Следовательно, на основании достаточного признака сходится и данный ряд. ●
Пример 2. Рассмотрим знакочередующийся ряд
,
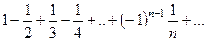который сходится по признаку Лейбница. Но ряд, составленный из абсолютных величин данного ряда
является гармоническим и, следовательно, расходится.●
Определение 1. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.
Определение 2. Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Ряд, рассмотренный в примере 1, является абсолютно сходящимся, в примере 2 – условно сходящимся.
Теорема 1. Сумма абсолютно сходящегося ряда не меняется от любой перестановки его членов.
Теорема 2. Два абсолютно сходящихся ряда можно перемножать по правилу умножения конечных сумм. Полученный в результате умножения ряд абсолютно сходится и его сумма равна произведению сумм исходных рядов.
Остаток ряда и его оценка
Рассмотрим сходящийся ряд
(1)
Его сумма 
, где 
.
Определение. Разность между суммой ряда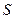 
и его 
-ой частичной суммой 
называется -ым остатком сходящегося ряда.
Остаток ряда обозначается 
:
Абсолютная погрешность при замене суммы ряда 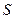его частичной суммой равна модулю остатка ряда:
.
Таким образом, если требуется найти суму ряда с точностью до 
, то надо взять сумму такого числа первых членов ряда, чтобы выполнялось неравенство 
.
Теорема. Если знакочередующийся ряд сходится по признаку Лейбница, то его -ый остаток по абсолютной величине не превосходит первого из отброшенных членов:
.
Пример. Найти с точностью до 10-3 сумму ряда 
.
Ряд сходится, т. к. удовлетворяет всем условиям признака Лейбница.
По правилу оценки погрешности вычисления надо взять столько членов, чтобы выполнялось неравенство
.
Тогда остаток ряда, начинающийся с этого члена, будет также меньше 10-3.
Следовательно, решаем неравенство:
.
Это неравенство удовлетворяется уже при 
: 
.
Следовательно, начиная с члена 
, можно отбросить все члены ряда и вычислить только первыепять членов ряда.
.●
