Приведённые кинетостатические зависимости раскрывают основные закономерности движения системы гонщик-велосипед и создают предпосылки для более глубокого анализа отдельных проблем. К таким проблемам можно отнести сравнение кинематических возможностей двух гонщиков, отличающихся, например, массой и телосложением (а следовательно, на систему гонщик-велосипед будут действовать разные по величине гравитационные и аэродинамические силы), или сравнительные оценки сил трения качения колёс в зоне контакта однотрубок с поверхностью дороги. Необходимо отметить, что исходные данные (коэффициенты трения качения, кинематической вязкости воздуха, аэродинамического сопротивления, площади миделя и другие параметры системы гонщик-велосипед), получаемые, как правило, экспериментальным путём, содержат значительные погрешности. Уменьшить влияние этих погрешностей можно, если проводить испытания двух сравниваемых систем, оценивая только конечны результат, как это делается при свободном движении двух гонщиков на спуске (оценивается длина свободного выбега)
Спуск – один из важнейших моментов шоссейной гонки, и квалифицированный гонщик стремится использовать его для обострения спортивной борьбы. Педалируя на больших передачах или на малых, но периодически с высокой частотой (малыми сериями), гонщик одновременно использует возможность увеличения скорости за счёт действия гравитационной силы, вызывающей движение велосипеда на спуске. К силам внешнего сопротивления необходимо относить силу аэродинамического сопротивления, силы трения качения колёс по поверхности дороги, силы трения качения в шарикоподшипниках втулок, силы трения однотрубок о поверхность дороги и силы аэродинамического сопротивления набора колёс.
Для того чтобы упростить задачу расчёта максимально возможных скоростей движения системы гонщик-велосипед при свободном спуске, исключим из рассмотрения силы трения качения в подшипниках и ограничимся приближенной оценкой аэродинамического сопротивления

Согласно схеме, уравнение действующих сил, согласно схеме можно записать в виде
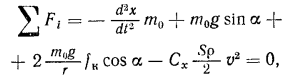
Где m0 – масса системы гонщик-велосипед, в (кг); “a” – угол наклона полотна шоссе, в градусах; g – ускорение свободного падения, м/c2; fк – коэффициент трения качения колеса велосипеда по поверхности полотна шоссе, м; r – радиус колеса, м; Cx – коэффициент аэродинамического сопротивления системы гонщик-велосипед, м2; p – кинематический коэффициент вязкости воздуха, Н*c2/м4; v – скорость движения системы гонщик-велосипед при свободном спуске (относительная скорость с учётом встречного или попутного ветра), м/c.
Согласно предыдущему уравнению с учётом cos”a”=1:

Введя обозначения
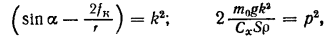
Получим
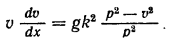
Разделяя переменные  и интегрируя обе части равенства, найдём
и интегрируя обе части равенства, найдём

Где при x=0 и v=0 постоянная интегрироваия С1=lnp2.
После подстановки значения C1 в уравнение выше получим
 или
или 
Откуда
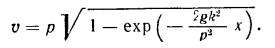
При X->inf имеем V->Vmax=p. Следовательно, максимально достижимая скорость свободного движения системы гонщик-велосипед на спуске при рассмотренных выше условиях и с учётом указанных допущений будет определяться уравнением

Общее уравнение, описывающее изменение скорости в процессе разгона системы на спуске, в функции пройденного пути имеет вид

При массе гонщика 72кг, массе велосипеда 10кг, общей массе системы m0=72+10=82кг, отсутствии ветра, p=1,25 Н*с2/m4; Cx=0.8, S=0,5м2, r=0,34м, g=9,81 м/с2, fк=4*10-3м и “a”=10 градусов максимально достижимая скорость движения составляет 22,26 м/с или 80,16 км/ч.
Гонщику трудно контролировать момент достижения максимальной скорости. Поэтому полезно знать примерно расстояние и время, когда такая скорость будет достигнута. Для исследования изменения скорости в функции времени преобразуем уравнение

Разделяя вновь переменные  и интегрируя обе части равенства, получим
и интегрируя обе части равенства, получим

Откуда при t=0 и v=0 находим C1=0. Следовательно,

Окончательно выражение для текущего значения скорости имеет следующий вид:

Ряд решений этого уравнения при различных уклонах дороги представлен на рисунке ниже

Отсюда видно, что для достижения максимально возможных скоростей при свободном спуске необходимо значительное время и расстояние. Потому гонщик в целях достижения максимального спортивного результата должен форсировать разгон на спусках с использование увеличенных передач или педалирования короткими сериями.




