
Рассмотрим движение системы гонщик-велосипед, сохранив для колёс и действующих на них сил прежние обозначения, а массу гонщика и велосипеда обозначим через m3 и сосредоточим её в точке с координатами x3 и y3. Общая масса всей системы: m0=m1+m2+m3 будет сосредоточена в центре масс ЦМ с координатами x0 и y0. Уравнения движения с учётом общей массы m0 и силы аэродинамического сопротивления Fc, приведённой к центру массы системы, имеют вид:

Считая y1=0, x1=r1ф1 и x2=r2ф2, получим уравнение движения центра масс

где

Интегрируя в пределах от 0 до t, получим уравнение энергетического баланса в следующем виде:

Левая часть уравнения выражает приращение кинетической энергии системы, первый член правой – работу движущего момента, а остальные члены – соответственно работу на преодоление сил трения качения, работу сил тяжести и работу сил сопротивления воздуха. Для конкретного использования уравнения функцию x1(t) представим в следующем виде:
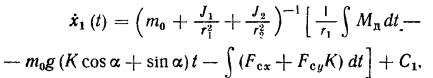
Где произвольную постоянную С1 найдём из условия x1(0)=x10
Движущий момент Мд в первом приближении является заданной функцией времени, зависящей от техники педалирования гонщика и условий движения. В общем виде это достаточно сложная функция, и количественные закономерности движения аналитически получить затруднительно.
Ограничимся только качественным анализом движения системы, приняв заком изменения движущего момента в виде

Где М0 – среднеинтегральное значение движущего момента; delta(M) – амплитуда изменения этого момента; p – круговая частота изменения движущего момента.
Приняв значения Fcx и Асy постоянными, из уравнения конкретного использования функции приращения кинетической энергии с параметром x1(t) получим

Из уравнения следует, что если сумма коэффициентов при t больше нуля, то скорость с течением времени будет возрастать и наоборот. Поэтому движение с постоянной средней скоростью должно характеризоваться зависимостью

Из этого уравнения следует, что амплитуда колебаний скорости уменьшается с увеличением массы системы и моментов инерции колёс. Кроме того, поскольку частота p может быть принята пропорциональной скорости x1(t), то можно сделать вывод, что с ростом скорости x1(t) неравномерность хода уменьшается при прочих равных условиях.
Зная закон изменения ускорения системы, можно определить реакции N1 и N2, для чего необходимо приложить к центрам масс m1, m2 и m3 соответствующие силы инерции и использования условия равновесия системы. После преобразований получим

Где  L – база велосипеда, x0, y0 – координаты центра масс системы.
L – база велосипеда, x0, y0 – координаты центра масс системы.
Из преобразованного уравнения следует, что реакция N2, действующая на переднее колесо велосипеда, уменьшается при ускоренном движении (x>0) и на цчастках подъёма (“a”>0) и зависит от соотношения радиусов r1 и r2 колёс велосипеда. В то же время уменьшение реакции N2 всегда приводит к увеличению реакции N1, действующей на заднее, ведущее колесо.
Полученные результаты относятся к движению по прямолинейному участку дороги, когда процесс педалирования является установившимся. Движущий момент Мд пропорционален усилию Q, приложенному к педали по касательной к траектории её движения. Мощность Qx1(t), развиваемая гонщиком, является ограниченной величиной, она не может превзойти некоторые значения Pmax, т.е. 






