Москва 2011
Оглавление:
1. Структура системы гонщик-велосипед
2. Кинематика системы в целом
3. Кинематика колеса
4. Кинетостатика системы
5. Система гонщик-велосипед в целом
6. Сравнительные оценки на основе кинетостатических зависимостей.
7. Динамика системы гонщик-велосипед
Структура системы гонщик-велосипед
Сама система состоит из двух объектов – управляющего и управляемого – и ряда таких внешних условий, как аэродинамические, механические и кинематические воздействия. Управляющий объект – гонщик, воспринимая информацию о состоянии дорожного покрытия, кинематических (траектория, скорость, ускорение), аэродинамических, тактико-технических и других условий гонки, формирует с помощью центральной нервной системы (ЦНС) целенаправленное воздействие на объект управления таким образом, чтобы создать наиболее эффективные условия передачи энергии от биологического двигателя – гонщика к потребителю – велосипеду в целях достижения наивысшего спортивно-технического результата.
Функция педалирования характеризуется двумя параметрами: крутящим моментом, определяемым касательной силой при педалировании, и частотой педалирования, совокупность которых является своеобразной амплитудно-частотной характеристикой гонщика. Регулятором совмещённого действия этих двух факторов является переключатель скоростей на шоссейном велосипеде или предварительно установленные звёздочки на трековом велосипеде. Такой регулятор позволяет получать рациональные передаточные отношения, с использованием которых гонщик может в экстремальные моменты гонки развивать максимальную мощность, а в остальные периоды гонки педалировать с минимальными затратами энергии. Учитывая, что шоссейные гонки продолжаются в течении нескольких часов, целенаправленное управление функциональными действиями гонщика приобретает решающее значение.
Функция управления фактически сводится к трём основным процессам: маневрированию (с учётом поддержания равновесного устойчивого движения системы), торможению и переключению скоростей. Обратная связь по каналам этой функции осуществляется с использованием параметров и характеристик трассы гонки.
В действительности все элементы рассматриваемой системы сами по себе представляют весьма сложные и недостаточно изученные объекты, между которыми осуществляются многоканальные связи, позволяющие реализовывать гармоничные и близкие к оптимальным действия гонщика по достижению наивысшего спортивно-технического результата.
Кинематика системы в целом
Траектория движения системы гонщик-велосипед ограниченна трассой – поверхностью трекового полотна, шоссе или кроссовой дороги. Во всех случаях, за исключением свободного полёта при преодолении препятствий, движение велосипеда полагает непрерывный контакт с поверхностью трассы. Именно этот контакт лежит в основе механики движения велосипеда и его управления.
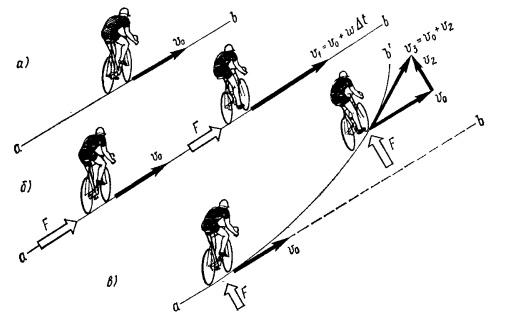
Согласно законам механики, изменения скорости и направления движения системы гонщик – велосипед не могут происходить без воздействия на неё внешних сил. При отсутствии последних система стремится сохранить состояние покоя или равномерного прямолинейного движения. В этом случае вектор скорости системы V0 совпадает с направлением движения ab, что мы и видим на рисунке. Для изменения скорости и направления движения системы необходима внешняя сила F, тем большая, чем больше масса системы m и ускорение w, которое ей требуется сообщить. Масса системы является мерой её инертности, т.е. способности сохранять неизменными параметры движения. Так, при воздействии внешней силы F со стороны дорожного покрытия в зоне контакта ведущего колеса с дорогой система получает ускорение w в течении времени дельта(T)и скорость движения становится равной V1=V0+w*дельта(T)
Действие внешней силы способно изменить не только скорость, но и направление движения. Так, под действием силы F, направленной перпендикулярно к траектории движения, система приобретает дополнительную скорость V2. Суммарная скорость V3=V0+V2, будучи суммой двух векторов, является скоростью движения системы по траектории ab’ в отличии от скорости V0 прямолинейного движения.
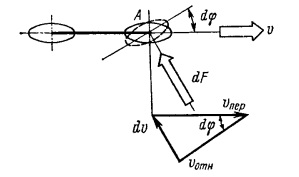Таким образом, только наличие внешней силы позволяет осуществить поворот велосипеда, т.е. изменить траекторию движения системы. Для анализа действия этой системы будем считать, что велогонщик, двигаясь прямолинейно со скоростью V (как показано на схеме оценки условий, обеспечивающих поворот велосипеда), повернул руль в точке A на угол dф. Пусть этот поворот осуществлен в момент времени t. Можно считать, что в момент времени t+dt переносная скорость системы Vпер в силу закона инерции практически не изменится ни по величине, ни по направлению. При повороте на угол dфабсолютная скорость точки A контакта колеса с дорогой уже не равна нулю, так как переносная скорость оси Vпер и относительная скорость Vотн точки A колеса не лежит на одной прямой. Скорость точки A становится равной dvи направлена в сторону угла поворота dф.
Для изменения скорости движения на величину dvнеобходимо приложить внешнее усилие, которым может быть только сила трения колеса о поверхность дороги. Следовательно, при повороте колеса появляется сила трения dF, действующая на колесо в направлении dv, чем и обеспечивается необходимое ускорение системы. Очевидно, что при отсутствии сил трения или при недостаточных их значениях контролируемый поворот становится невозможным.
Практика показывает, что одновременно с поворотом необходимо осуществить наклон велосипеда в сторону центра кривизны, чтобы компенсировать центробежные силы инерции. Требуемый угол наклона Ѱ приближенно можно определить из известного равенства:
Где [u] – допустимое значение коэффициента сцепления колеса с дорожным покрытием; R – радиус кривизны виража, v – скорость движения; g – ускорение свободного падения. Это равенство получено на основании анализа сил, возникающих в системе гонщик – велосипед при прохождении поворота с плоским дорожным покрытием, как показанно на рисунке ниже.
Ясно, что гонщик должен находиться вертикально, иначе он упадёт. Но его вертикаль aa не совпадает с земной Oy, она наклонена под некоторым углом ф, который не зависит от массы m гонщика, а зависит от радиуса кривизны поворота и скорости его прохождения. Однако масса системы определяет величину силы реакции N дорожного полотна на колёса велосипеда и величину силы трения F в зоне контакта колеса с дорогой. Устойчивость системы гонщик-велосипед обеспечивается балансом моментов центробежной силы F(u)=mv2/Rи гравитационной силы Fг=mg.
Для обеспечения предельной скорости прохождения виража, определяемой допустимым значением [u], применяют приём смещения центра масс (ЦМ) системы в сторону, противоположную центру кривизны виража. Это позволяет сместить ЦМ вниз на величину дельтаY=Y1-Y2, что, однако, не изменяет условий взаимодействия системы с поверхностью дороги, определяемых углом Ѱ. Максимально возможные скорости прохождения виражей при различных покрытиях и состоянии дороги показаны на рисунке ниже. Аналогичный анализ может быть проведён и для условий прохождения наклонных виражей велосипедного трека, что на указано на таблице, где система координат x1Oy1 полотна трека развёрнута на угол B относительно горизонта.
В зависимости от скорости движения системы радиус кривизны R траектории движения ЦМ изменяется от Rmax при V=0 до Rmin при V=Vmax. Уравнение угла наклона в данном случае требует уточнения в связи с учётом радиуса кривизны траектории движения ЦМ системы гонщик-велосипед. В таком случает скорость прохождения виража в зависимости от угла Ф выразится уравнением 
Это уравнение приближенно описывает мгновенное значение скорости движения в данной точке виража. Общая картина изменения кинематических характеристик системы при прохождении виражей значительно сложнее и зависит от целого ряда параметров: таких, как радиус кривизны виража, координаты его положений, профиль виража, вид покрытия его поверхности, механические характеристики системы гонщик-велосипед.
Приёмы прохождения плоского виража существенно отличаются от приёмов прохождения наклонного виража.
Кинематика колеса.
Движение колеса имеет сложную структуру. Колесо перекатывается по поверхности дороги теоретически без проскальзывания, в то время как в действительности проскальзывание существует, но составляет сравнительно небольшую величину.
Введём три системы координат: xy – неподвижную относительно поверхности дороги; x1y1 – подвижную относительно поверхности дороги; x1y1 – подвижную и связанную с рамой велосипеда или осью колеса, x2y2 – подвижную и связанную непосредственно с колесом, которая, таким образом, совершает сложное движение. Система координат x1y1 совершает переносное поступательное движение, в котором все точки имеют одинаковую скорость V. Система координат x2y2 совершает относительное вращательное движение, в котором каждая точка колеса движется с окружной скоростью Vp = wp, где w – угловая скорость относительного движения; p – расстояние от начала координат O1 до рассматриваемой точки. Векторная сумма переносной и относительной скоростей любой точки колеса равна абсолютной скорости Va=V+Vp
Точка C является точкой касания колеса с поверхностью дороги и является неподвижной при принятом выше условии – отсутствии проскальзывания колеса относительно дороги и деформации однотрубки. Скорость точки С, принадлежащей колесу (p=R), равна
Для произвольной точки E колеса, находящейся на расстоянии p=O1E от оси колеса, скорость определится как векторная сумма Ve=V+VpE. Численное значение скорости точки E может быть определено с помощью выражения
С другой стороны, плоскопараллельное движение колеса в каждый момент времени можно представить как вращение около мгновенного центра вращения. В данном случае мгновенным центром вращения является мгновенный центр скоростей в точке C, в котором скорость равна нулю. Положение мгновенного центра скоростей можно определить также как точку пересечения перпендикуляров к направлениям векторов абсолютных скоростей двух произвольных точек колеса, например А и Е.
Тогда скорость любой точки колеса определяется выражением V=wp, где W – угловая скорость вращения колеса вокруг мгновенного центра скоростей, равная угловой скорости вращения колеса вокруг своей оси O1; p – расстояние от рассматриваемой точки до мгновенного центра вращения. Так, для точки D это расстояние составляет Pd=2R, для точек A и B будет Pв=Pа=Rsqrt2; для произвольной точки Е
Направлен вектор абсолютной скорости в сторону вращения перпендикулярно к соответствующему отрезку P, соединяющему мгновенный центр скоростей с рассматриваемой точкой.
Окружная скорость любой i-й точки Vri направлена по касательной к траектории её движения относительно оси вращения колеса O1. По мере увеличения угла “a” точка A последовательно занимает положения C, B и D, а вектор Vri, оставаясь постоянным по величине, меняет своё направление. Это объясняется наличием нормального ускорения движения даже при равномерном вращении колеса, т.е. при тангенциальном ускорении, равном нулю. При бесконечно малом угле поворота delta(a), на который колесо поворачивается за бесконечно малый промежуток времени delta(t), скорости в точках K и K1 представляют собой равные по величине векторы Vrk и Vrk1, касательные к окружности в этих точках. Перенеся вектор скорости Vrk в точку K1 получим вектор delta(V), представляющий собой изменение скорости точки K при переходе в положение K1 за время delta(t). Из подобия треугольников и с учётом того, что delta(t)->0, можно записать
Отсюда следует, что нормальное ускорение точки K
Это ускорение направлено к центру колеса и называется центростремительным. В случае неравномерного движения полное ускорение складывается из нормального и тангенциального, которые взаимно перпендикулярны: 
Кинетостатика системы
При движении велогонщик и велосипед образуют единую движущуюся систему, в которой силы взаимодействия являются внутренними и сами по себе не могут обеспечить движения общего центра масс системы. Для движения необходимы внешние силы, которые в данном случае сводятся к силам тяжести, силам трения колёс о дорожное покрытие и силам аэродинамического сопротивления.
Для начала рассмотрим отдельно взятые ведущее и ведомое колёса велосипеда, а затем систему гонщик-велосипед в целом.
Ведущее колесо.
К ведущему колесу массой m1 с моментом инерции J1 приложен движущий момент Mд, под действием которого со стороны дороги возникает сила трения скольжения F1=fN1, где N1 – сила нормального давления; f – коэффициент трения скольжения. Точка A1 является мгновенным центром вращения и её скорость равна нулю. Поэтому f есть коэффициент трения покоя, величина которого неопределенна и может принимать значения от 0 до fmax. Эпюра скоростей 1 в диаметральном сечении колеса A1B1 является фактически эпюрой скоростей набегающего воздушного потока, сила сопротивления которого Fe, приложенная в центре масс эпюры 2 суммарного лобового и вихревого сопротивлений, создаёт момент полного аэродинамического сопротивления Мe.
Колесо, имеющее пневматическую шину в виде однотрубки, деформируется в зоне контакта с поверхностью дороги, что приводит к смещению реакции N1 на некоторую величину fк, называемую коэффициентом трения качения Mк1=fкN1. Учитывая малось величины fк, в дальнейшем будем считать реакцию N1 приложенной в точке A1.
Уравнения движения колеса запишутся в виде системы:
Где x1, y1 – координаты положения оси колеса O1; Ф1 – угол поворота ведущего (заднего) колеса; “a” – угол наклона поверхности дороги к горизонтали.
Если колесо катится без проскальзывания, то x1=r1Ф1; y1=0; N1=m1g*cos”a”. Сила трения F1 без учёта сил аэродинамического сопротивления
Движущий момент Mд в правой части уравнения может принимать различные значения, но если правая часть уравнения станет больше, чем fmax N1, то появится проскальзывание колеса относительно дороги и увеличение Mд оказывается нецелесообразным. Максимальное ускорение составляет величину
Характерно, что под уклон (“a”<0) можно обеспечить движение без проскальзывания с большими ускорениями.
Ведомое колесо
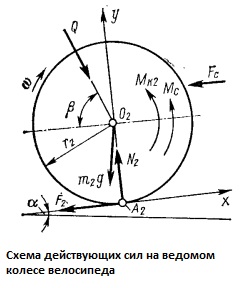
Движение ведомого колеса массой m2 с моментом инерции J2 происходит под действием силы Q, приложенной со стороны передней вилки рамы велосипеда. В соответствии с схемой действующих сил на ведомом колесе уравнения движения имеют вид:
где х2, у2 - координаты положения оси колеса 0 2; ф2 - угол поворота ведомого (переднего) колеса; р - угол наклона линии передней вилки к горизонтали. Из системы уравнений в случае y2=0, N2=Q*sinB+m2g*cos”a” при отсутствии аэродинамического сопротивления и проскальзывания колеса относительно дороги, т.е. при x2=r2ф2, получим силу трения
Если в уравнении отсутствует скольжение, должно выполняться условие F2<=fmaxN2. Максимальное ускорение
В уравнение необходимо подставлять значение Q, определяемое из предыдущего уравнения при F2=faxN2.
Рассмотренные случаи показывают исключительно важную роль сил трения скольжения при движении колёс. Так, для ведущего колеса при отсутствии трения скольжения (F1=0) движение из состояния покоя невозможно при “a”=0, а при “a”>0 ускорение x направлено в обратную сторону. Для ведомого колеса при F2=0 невозможно его вращение из состояния покоя. Кроме того, от сил трения скольжения зависят максимальные ускорения, которые можно сообщить центрам масс колеса при отсутствии проскальзывания.
