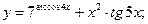Мета роботи: навчитись обчислювати границі функцій, розкривати невизначеності
Наочне забезпечення та обладнання:
1. Інструкційні картки;
2. Приклади задач;
3. Роздаткові матеріали: варіанти завдань
4. Обчислювальні засоби.

Теоретичні відомості про границю функції
Означення. Нехай х 0Î(а, b) і функція у = f (x) визначена на інтервалі (а, b) за винятком, можливо, точки х 0. Якщо для будь-якої збіжної послідовності хn (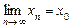 ,
,  ) існує
) існує  , то говорять, що функція
, то говорять, що функція  має границю А при
має границю А при  .
.
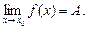
Якщо існують границі 
то виконуються такі співвідношення:
1)  ,
,
2)  ,
,
3) 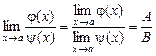 , якщо
, якщо  .
.
Задача №1. Знайти границю функції:
а) 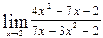 ; б)
; б)  ; в)
; в)  .
.

Теоретичні відомості про визначні границі
1. 
2. 
Задача №3. Знайти границю функції: а)  ; б)
; б) 
Питання для самоперевірки знань, умінь
1. Що називається границею функції в точці?
2. Як пов’язані границя і неперервність функції та її границя?
3. Визначні границі.
4. Як розкрити невизначеності  ;
; 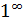 ?
?
Висновок__________________________________________________
Перевірив викладач ___________ Оцінка___________ Дата ___________
Виконаємо самостійно
В-1 В-2
1. Знайти границю функції:
а) 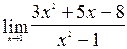 ; а)
; а)  ;
;
б)  ; б)
; б)  ;
;
в)  ; в)
; в)  ;
;
г)  ; г)
; г) 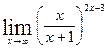 .
.
В-3 В-4
1. Знайти границю функції:
а)  ; а)
; а)  ;
;
б)  ; б)
; б)  ;
;
в)  ; в)
; в)  ;
;
г) 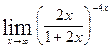 ; г)
; г)  .
.
В-5 В-6
1. Знайти границю функції:
а)  ; а)
; а) 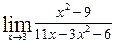 ;
;
б)  ; б)
; б)  ;
;
в)  ; в)
; в) 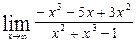 ;
;
г) 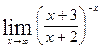 ; г)
; г)  .
.
ТЕМА 5. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ
ПРАКТИЧНА РОБОТА № 7
Тема. Обчислення похідних функцій. Обчислення похідних складених функцій
Мета роботи: навчитись обчислювати похідні функцій, похідні складених функцій.
Наочне забезпечення та обладнання:
1. Інструкційні картки;
2. Приклади задач;
3. Роздаткові матеріали: опорні конспекти “Основні формули диференціювання”, варіанти завдань.
4. Обчислювальні засоби: калькулятор.

Теоретичні відомості про правила диференціювання
Нехай U та V – диференційовані функції, С-стала, тоді:
1. 
2. 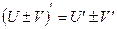
3. 
4. 
Якщо 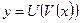 - складена функція, то
- складена функція, то 
Основні формули диференціювання.
1.  9.
9. 
2.  10.
10. 
3.  11.
11. 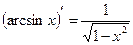
4. 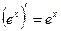 12.
12. 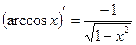
5.  13.
13. 
6.  14.
14. 
7. 
8. 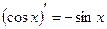
Задача №1. Знайти похідну функції:
a) 
б)