ПРАКТИЧНА РОБОТА № 11
Тема. Основні поняття та означення функції багатьох змінних. Частинні похідні. Екстремуми функції багатьох змінних. Необхідна умова існування точок екстремуму.
Мета роботи: засвоїтиозначення функції двох змінних, правила дослідження на екстремум; навчитись проводити дослідження функції двох змінних на екстремум; застосовувати здобуті навички для розв’язування прикладних задач економічного змісту.
Наочне забезпечення та обладнання:
1. Інструкційні картки;
2. Приклади задач;
3. Роздаткові матеріали: опорні конспекти “ Диференціювання функцій багатьох змінних”
4. Обчислювальні засоби: калькулятор.
Теоретичні відомості про правила диференціювання.
Функцією двох змінних  ,
, 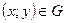 називається функція, яка кожній парі чисел
називається функція, яка кожній парі чисел 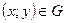 ставить у відповідність деяке число
ставить у відповідність деяке число  .
.
Аналогічно означається функція трьох і більше невідомих.
Частинні похідні.
 - це похідна по
- це похідна по 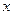 функції
функції  при фіксованому
при фіксованому 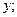
 - це похідна по
- це похідна по  функції
функції  при фіксованому
при фіксованому 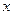 .
.
Частинні похідні функції знаходять за звичайними правилами диференціювання; потрібно тільки при диференціюванні по 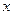 змінну
змінну  вважати сталою, а при диференціюванні по
вважати сталою, а при диференціюванні по  вважати
вважати 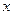 сталою.
сталою.
Якщо 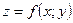 , то
, то 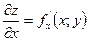 ;
; 
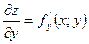 - частинні похідні першого порядку.
- частинні похідні першого порядку.
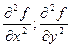 - частина похідної другого порядку.
- частина похідної другого порядку.
 - мішані похідні другого порядку.
- мішані похідні другого порядку.
Якщо мішані похідні неперервні, то вони рівні.
Задача №1. Знайти частинні похідні першого і другого порядків від заданих функцій:
а) z = 8e 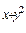 - 3xy
- 3xy  + 7x – 3
+ 7x – 3
б) z = xsiny + 8x 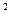 y
y 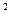 - 7x
- 7x
Задача 2. Знайти частинні похідні 1-го порядку та повний диференціал функції:
а) 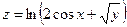
б) 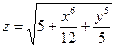
в) 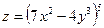
г) 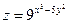
Задача 3. Обчислити наближено, за допомогою повного диференціала 
Питання для самоконтролю знань, умінь.
1. Означення функції двох змінних (трьох та більшого числа змінних).
2. Неперервність функції.
3. Частинні похідні функції двох змінних.
4. Частинні похідні другого порядку. Мішані частинні похідні.
5. Повний диференціал
Висновок __________________________________________________________
____________________________________________________________________
Перевірив викладач ___________ Оцінка _________ Дата ___________
Виконаємо самостійно
В-1 В- 2
1.Знайти частинні похідні першого і другого порядку та повний диференціал функції.
 ;
; 
2. Знайти частинні похідні першого порядку функцій:
а) 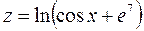 а)
а) 
б) 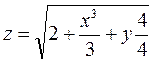 б)
б) 
3. Обчислити наближено за допомогою повного диференціала:
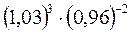
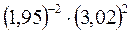
В-3 В- 4
1.Знайти частинні похідні першого і другого порядку та повний диференціал функції.

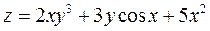
2. Знайти частинні похідні першого порядку функцій:
а) 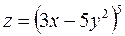 а)
а) 
б)  б)
б) 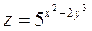
3. Обчислити наближено за допомогою повного диференціала:
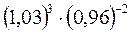
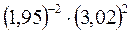
В-5 В- 6
1. Знайти частинні похідні першого і другого порядку та повний диференціал функції.
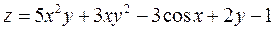
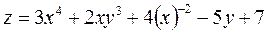
2. Знайти частинні похідні першого порядку функцій:
а)  б)
б) 
а)  б)
б) 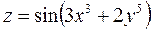
3. Обчислити наближено за допомогою повного диференціала:
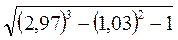
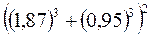
В-7 В- 8
1.Знайти частинні похідні першого і другого порядку та повний диференціал функції.
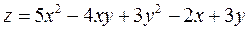
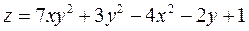
2. Знайти частинні похідні першого порядку фу






