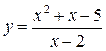б) Знайти наближене значення 
Питання для самоконтролю знань, умінь
1. Похідна суми, добутку, частки двох функцій.
2. Похідна складеної функції.
- Похідна степеневої функції.
- Похідні логарифмічної, показникової та тригонометричних функцій.
- Що називається диференціалом?
- Геометричний зміст диференціала
- Як за допомогою диференціала можна знайти наближене значення приросту функції?
- Як обчислити наближене значення функції за допомогою диференціала?
Висновок__________________________________________________
Перевірив викладач ___________ Оцінка ___________ Дата___________
ПРАКТИЧНА РОБОТА № 11
Тема. Схема дослідження і побудови графіка функції за допомогою похідної
Мета роботи: навчитись проводити дослідження функції та будувати її графік.
Наочне забезпечення та обладнання:
1. Інструкційні картки;
2. Приклади задач;
3. Роздаткові матеріали: опорні конспекти “Основні формули диференціювання”
4. Обчислювальні засоби: калькулятор.
Теоретичні відомості. Загальна схема дослідження і побудови графіка функції. Алгоритм дослідження функції та побудови графіка
1. Область визначення функції, точки перетину з вісями координат.
2. Дослідження функції на парність, непарність.
3. Знаходження асимптот графіка функції.
Означення. Пряма y= kx+b, де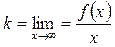 
, 
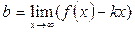, називається похилою асимптотою кривої y= f(x).
4. Дослідження функції на монотонність, екстремум.
5. Дослідження на опуклість (вгнутість) та точки перегину графіка функції.
6. Побудова графіка функції
Задача №1. Дослідити та побудувати графік функції 
Задача №2. Дослідити та побудувати графік функції 
