Нехай дано систему n лінійних рівнянь з n невідомими
(1)
Запишемо дану систему у вигляді матричної рівності:
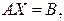(2)
де 
- квадратна матриця n-го порядку, складену з коефіцієнтів при невідомих (її називають матрицею системи);
матриця розмірності (n×1), складена з невідомих;
матриця розмірності (n×1), складена з вільних членів.
Тобто:
Розв’язати систему (1) означає знайти такі значення невідомих 
які перетворюють в істинні рівності одночасно всі рівняння системи. Це теж саме, що знайти невідому матрицю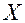 
, яка перетворює в істинну рівність матричне рівняння (2).
Систему лінійних рівнянь називають не виродженою, якщо матриця системи не вироджена, тобто detA≠0. Невироджена система лінійних рівнянь має єдиний розв’язок.
Розв’язок невиродженої системи лінійних рівнянь, записаної у вигляді матричного рівняння знаходять за формулою:
де 
- матриця, обернена до матриці 
Задача 3. Розв’язати систему лінійних рівнянь матричним способом:
a) 
Питання для самоперевірки знань, умінь
1. Визначники матриць другого та вищих порядків.
2. Поняття системи n лінійних рівнянь відносно n невідомих.
3.Формули Крамера. Суть методу Крамера розв’язування систем лінійних рівнянь, його недоліки.
4. Метод Гауса розв’язування систем лінійних рівнянь. В чому полягає його універсальність?
5. Розв’язування систем за допомогою оберненої матриці. Які системи можна розв’язати за допомогою оберненої матриці?
Висновок____________________________________________________________
__________________________________________________________________
Перевірив викладач ___________ Оцінка___________Дата ______________
ТЕМА 2. ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ
ПРАКТИЧНА РОБОТА № 3
Тема. Застосування скалярного, векторного та мішаного добутків до розв’язування прикладних задач
Мета роботи: навчитись виконувати дії над векторами, застосовувати скалярний, векторний та мішаний добутки до розв’язування прикладних задач.
Наочне забезпечення та обладнання:
1. Інструкційні картки;
2. Індивідуальні завдання;
3. Роз даткові матеріали: “Основні формули аналітичної геометрії”
4. Обчислювальні засоби.
