Определители составили:  ;
;  ;
;  . По их значениям рассчитаны параметры и получено уравнение тренда:
. По их значениям рассчитаны параметры и получено уравнение тренда: 
 . Уравнение тренда выявляет тенденциюпостепенного снижения и сохранения на неизменном уровне численности занятых. Индекс корреляции оценивает выявленную связь как тесную:
. Уравнение тренда выявляет тенденциюпостепенного снижения и сохранения на неизменном уровне численности занятых. Индекс корреляции оценивает выявленную связь как тесную:  (см. гр. 7 и 8). Здесь изменения численности занятых на 73,3% определены изменениями систематических факторов, а на 26,7% - прочими причинами. Ошибка аппроксимации очень невелика
(см. гр. 7 и 8). Здесь изменения численности занятых на 73,3% определены изменениями систематических факторов, а на 26,7% - прочими причинами. Ошибка аппроксимации очень невелика  =2,7% (гр. 9) и поэтому возможности дальнейшего использования модели будут зависеть от оценки корреляции отклонений.
=2,7% (гр. 9) и поэтому возможности дальнейшего использования модели будут зависеть от оценки корреляции отклонений.
Коэффициент корреляции отклонений (коэффициент автокорреляции) выявил их заметную связь ( ), которая является статистически незначимой:
), которая является статистически незначимой: 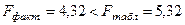 , то есть нулевая гипотеза
, то есть нулевая гипотеза  может быть принята с 5%-ой вероятностью допустить ошибку. Таким образом, имеются веские основания для использования модели равносторонней гиперболы для выполнения прогнозных расчётов.
может быть принята с 5%-ой вероятностью допустить ошибку. Таким образом, имеются веские основания для использования модели равносторонней гиперболы для выполнения прогнозных расчётов.
При выполнении прогнозов на 2001, 2002, 2003 и 2004 годы подставим в уравнение прогнозные значения фактора,  12, 13, 14, 15, что позволяет получить результат на уровне 65,6 – 65,4 млн. чел.:
12, 13, 14, 15, что позволяет получить результат на уровне 65,6 – 65,4 млн. чел.:  ;
;  ;
;  ;
;  . В данном прогнозе реализуется гипотеза о стабилизации численности занятых и её сохранении на уровне 65,4 млн. чел.
. В данном прогнозе реализуется гипотеза о стабилизации численности занятых и её сохранении на уровне 65,4 млн. чел.
3. Рассмотрим возможность использования показательной кривой для описания тенденции и прогноза. Показательная форма тренда имеет вид  и предполагает выполнение процедуры линеаризации исходного уравнения с целью приведения его к линейному виду.
и предполагает выполнение процедуры линеаризации исходного уравнения с целью приведения его к линейному виду.  В расчёте параметров полученного линейного уравнения участвуют значения
В расчёте параметров полученного линейного уравнения участвуют значения  и
и  Порядок расчёта представим в табл. 4.
Порядок расчёта представим в табл. 4.
Расчёт определителей второго порядка даёт следующие результаты:



По ним рассчитаны параметры линеаризованной функции:
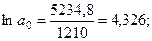
 и построено уравнение:
и построено уравнение:  . Для получения уравнения в естественной форме выполним процедуру потенцирования результатов:
. Для получения уравнения в естественной форме выполним процедуру потенцирования результатов:  .
.
Таблица 4.
| Годы | 
| 
| 
| 
| 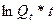
| 
| 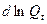
| 
| 
| 
| 
|
| 75,3 | 4,321 | 4,321 | 4,309 | 0,013 | 0,00017 | 74,3 | 1,0 | 1,4 | |||
| 73,8 | 4,301 | 8,603 | 4,291 | 0,010 | 0,00010 | 73,0 | 0,8 | 1,1 | |||
| 72,1 | 4,278 | 12,834 | 4,273 | 0,005 | 0,00003 | 71,8 | 0,3 | 0,5 | |||
| 70,9 | 4,261 | 17,045 | 4,256 | 0,006 | 0,00004 | 70,5 | 0,4 | 0,6 | |||
| 68,5 | 4,227 | 21,134 | 4,238 | -0,011 | 0,00012 | 69,3 | -0,8 | 1,1 | |||
| 66,4 | 4,196 | 25,174 | 4,220 | -0,025 | 0,00063 | 68,0 | -1,6 | 2,4 | |||
| 66,0 | 4,190 | 29,328 | 4,203 | -0,013 | 0,00017 | 66,9 | -0,9 | 1,3 | |||
| 64,7 | 4,170 | 33,358 | 4,185 | -0,015 | 0,00023 | 65,7 | -1,0 | 1,4 | |||
| 63,8 | 4,156 | 37,402 | 4,167 | -0,011 | 0,00012 | 64,5 | -0,7 | 1,1 | |||
| 64,0 | 4,159 | 41,589 | 4,149 | 0,009 | 0,00008 | 63,4 | 0,6 | 0,9 | |||
| 64,3 | 4,164 | 45,799 | 4,132 | 0,032 | 0,00102 | 62,3 | 2,0 | 3,0 | |||
| Итого | 749,8 | 46,422 | 276,587 | 46,422 | 0,0 | 0,00271 | 749,7 | 0,102 | 14,7 | ||
| Средняя | 68,16 | 4,220 | — | — | — | — | 0,00025 | — | — | 1,3 | |
| Сигма | 4,01 | 0,0581 | 3,162 | — | — | — | — | — | — | — | — |
| D | 16,08 | 0,00337 | 10,00 | — | — | — | — | — | — | — | — |
Показательный тренд установил, что численность занятых сокращается со среднегодовым темпом, равным 0,9825 или 98,3%. За период 1990-2001 гг. численность занятых ежегодно уменьшалась в среднем на 1,7%.
В данном случае, показатели тесноты изучаемой связи рассчитываются не как обычно – на фактических и расчётных значениях результата ( и
и  ), а с использованием линеаризованных значений результата
), а с использованием линеаризованных значений результата 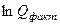 и
и  , потому что именно для них выполняется требование МНК о наименьшей сумме квадратов отклонений. Расчёт выполнен в гр.8 и 9.
, потому что именно для них выполняется требование МНК о наименьшей сумме квадратов отклонений. Расчёт выполнен в гр.8 и 9.
Выявлена весьма тесная зависимость численности занятых от комплекса систематических факторов:  . Уравнение и его параметры статистически значимы и надёжны, т.к. Fфакт.= 112, что значительно превосходит Fтабл.= 5,12 (при d.f.1=1; d.f.2=11-1-1=9; α=0,05).
. Уравнение и его параметры статистически значимы и надёжны, т.к. Fфакт.= 112, что значительно превосходит Fтабл.= 5,12 (при d.f.1=1; d.f.2=11-1-1=9; α=0,05).
Средняя ошибка аппроксимации в данной задаче рассчитывается как обычно, с использованием  и
и  , т. к. при решении прогнозных задач производится оценка естественных, а не линеаризованных значений результата. Ошибка мала:
, т. к. при решении прогнозных задач производится оценка естественных, а не линеаризованных значений результата. Ошибка мала:  =1,3% и поэтому модель может быть рекомендована для использования при прогнозировании. При этом, важно убедиться, что после выявления тренда формируются отклонения
=1,3% и поэтому модель может быть рекомендована для использования при прогнозировании. При этом, важно убедиться, что после выявления тренда формируются отклонения 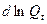 =
=  , представляющие собой значения случайной переменной.
, представляющие собой значения случайной переменной.
Для этого рассчитаем коэффициент автокорреляции отклонений:  . Расчёт выполняется по линеаризованным значениям результата, то есть, с иcпользованием
. Расчёт выполняется по линеаризованным значениям результата, то есть, с иcпользованием 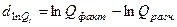 и
и  .
.
Необходимая для расчёта информация представлена в табл. 5.
По аналогии с предыдущими расчётами определим коэффициент автокорреляции через определители второго порядка для двух рядов отклонений: 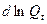 и
и  .
.
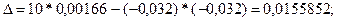
 ;
;

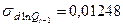 ;
; 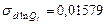 ;
;

 ;
; 


Таблица 5
  (Y) (Y)
|  (X) (X)
| 
| 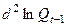
| |
| 0,013 | — | — | — | |
| 0,010 | 0,013 | 0,00013 | 0,00016 | |
| 0,005 | 0,010 | 0,00005 | 0,00011 | |
| 0,006 | 0,005 | 0,00003 | 0,00002 | |
| -0,011 | 0,006 | -0,00006 | 0,00003 | |
| -0,025 | -0,011 | 0,00027 | 0,00012 | |
| -0,013 | -0,025 | 0,00032 | 0,00060 | |
| -0,015 | -0,013 | 0,00019 | 0,00017 | |
| -0,011 | -0,015 | 0,00017 | 0,00023 | |
| 0,009 | -0,011 | -0,00011 | 0,00013 | |
| 0,032 | 0,009 | 0,00030 | 0,00009 | |
| Итого | -0,013 | -0,032 | 0,00129 | 0,00166 |
| Средняя | -0,0013 | -0,0032 | — | — |
| Сигма | 0,01579 | 0,0124841 | — | — |
| D | 0,0002493 | 0,0001559 | — | — |
Отклонения от показательного тренда находятся в заметной зависимости, которая, по оценке F -критерия, является статистически значимой и надёжной:  . Нулевая гипотеза о несущественной связи отклонений должна быть отвергнута с 5%-ой вероятностью ошибки. Это означает, что показательный тренд не является лучшим, т.к. не аккумулирует в себе влияния всего комплекса существенных факторов, а оставляет часть этого влияния в отклонениях от тренда. Поэтому показательный тренд не следует рассматривать как лучший.
. Нулевая гипотеза о несущественной связи отклонений должна быть отвергнута с 5%-ой вероятностью ошибки. Это означает, что показательный тренд не является лучшим, т.к. не аккумулирует в себе влияния всего комплекса существенных факторов, а оставляет часть этого влияния в отклонениях от тренда. Поэтому показательный тренд не следует рассматривать как лучший.
4. Остановимся на порядке построения и использования степенной модели в решении поставленных задач. В данной модели реализуется концепция мультипликативного механизма воздействия фактора на результат: 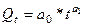 . Построению модели предшествует процедура линеаризации исходного уравнения п утём логарифмирования его элементов:
. Построению модели предшествует процедура линеаризации исходного уравнения п утём логарифмирования его элементов: 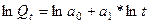 . В расчёте параметров участвуют
. В расчёте параметров участвуют  и
и  . Необходимая для расчёта исходная и промежуточная информация представлена в табл. 6.
. Необходимая для расчёта исходная и промежуточная информация представлена в табл. 6.
Расчёт определителей приводит к следующим результатам:
 ;
;
 ;
;
 .
.
Значения параметров линеаризованного уравнения составят:
 ;
;  ,
,
а уравнение линейное в линейной форме имеет вид:
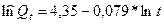 .
.
Таблица 6
| Годы | 
| 
| 
| 
| 
| 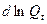
| 
|
| 0,000 | 4,321 | 0,000 | 0,000 | 4,346 | -0,025 | 0,00063 | |
| 0,693 | 4,301 | 0,480 | 2,981 | 4,291 | 0,010 | 0,00010 | |
| 1,099 | 4,278 | 1,207 | 4,700 | 4,259 | 0,019 | 0,00036 | |
| 1,386 | 4,261 | 1,922 | 5,907 | 4,236 | 0,025 | 0,00063 | |
| 1,609 | 4,227 | 2,590 | 6,803 | 4,219 | 0,008 | 0,00006 | |
| 1,792 | 4,196 | 3,210 | 7,518 | 4,204 | -0,009 | 0,00008 | |
| 1,946 | 4,190 | 3,787 | 8,153 | 4,192 | -0,002 | 0,00000 | |
| 2,079 | 4,170 | 4,324 | 8,671 | 4,182 | -0,012 | 0,00014 | |
| 2,197 | 4,156 | 4,828 | 9,131 | 4,172 | -0,016 | 0,00026 | |
| 2,303 | 4,159 | 5,302 | 9,576 | 4,164 | -0,005 | 0,00003 | |
| 2,398 | 4,164 | 5,750 | 9,984 | 4,156 | 0,007 | 0,00005 | |
| Итого | 17,502 | 46,422 | 33,400 | 73,424 | 46,422 | 0,000 | 0,00234 |
| Средняя | 1,591 | 4,220 | — | — | — | — | 0,00021 |
| Сигма | 0,710 | 0,058 | — | — | — | — | — |
| D | 0,505 | 0,0034 | — | — | — | — | — |
После процедуры потенцирования получаем уравнения в естественной форме:
 или иначе
или иначе 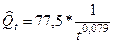 .
.
В модели нашло отражение единственная тенденция устойчивого сокращения численности занятых со снижающимся темпом этого сокращения. Если использовать модель для прогноза, то это будет прогноз снижения численности занятых, но при этом, процент её (численности) сокращения год от года будет уменьшаться.
Степенная модель выявляет связь, которая оценивается как весьма тесная и статистически значимая: 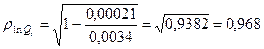 .
. 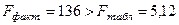 .
.
Особо отметим, что в данном случае, так же, как и при оценке тесноты связи показательной модели, расчёты общей и остаточной дисперсий проводятся по линеаризованным значениям признака-результата, то есть по 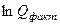 и
и 
Расчёт ошибки аппроксимации приводится в табл. 7. Её значение очень невелико и составляет 1,7%. При отсутствии автокорреляции в отклонениях от тренда степенная модель может использоваться для прогноза без формальных ограничений.
Таблица 7.
| Годы | 
| 
| 
| 
| 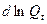
| 
| 
| 
|
| 77,2 | -1,9 | 3,6 | 2,8 | -0,025 | — | — | — | |
| 73,1 | 0,7 | 0,5 | 1,1 | 0,010 | -0,025 | -0,00025 | 0,000610 | |
| 70,8 | 1,3 | 1,7 | 2,0 | 0,019 | 0,010 | 0,00019 | 0,000101 | |
| 69,2 | 1,7 | 2,9 | 2,6 | 0,025 | 0,019 | 0,00047 | 0,000355 | |
| 67,9 | 0,6 | 0,4 | 0,8 | 0,008 | 0,025 | 0,00020 | 0,000617 | |
| 67,0 | -0,6 | 0,4 | 0,8 | -0,009 | 0,008 | -0,00007 | 0,000065 | |
| 66,2 | -0,2 | 0,0 | 0,2 | -0,002 | -0,009 | 0,00002 | 0,000074 | |
| 65,5 | -0,8 | 0,6 | 1,1 | -0,012 | -0,002 | 0,00003 | 0,000006 | |
| 64,9 | -1,1 | 1,2 | 1,6 | -0,016 | -0,012 | 0,00019 | 0,000139 | |
| 64,3 | -0,3 | 0,1 | 0,5 | -0,005 | -0,016 | 0,00008 | 0,000271 | |
| 63,8 | 0,5 | 0,3 | 0,7 | 0,007 | -0,005 | -0,00004 | 0,000025 | |
| Итого | 749,73 | 0,1 | 11,7 | 14,1 | 0,025 | -0,007 | 0,00083 | 0,002265 |
| Средняя | — | — | 1,06 | 1,3 | 0,0025 | -0,0007 | — | — |
| D | — | — | — | — | 0,01283 | 0,01503 | — | — |
В табл. 7 приводятся результаты проверки остатков на их автокоррелированность. В результате установлено, что в остатках существует умеренная связь, но она не является статистически значимой, то есть ряд отклонений представляют собой случайную переменную.
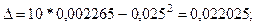

 ;
;  ;
; 
 ;
;  .
.
Следовательно, нулевая гипотеза о статистической незначимости взаимосвязи отклонений от степенного тренда должна быть принята, при том, что вероятность допустить ошибку не превысит общепринятого 5% уровня.
Следовательно, степенной тренд отражает влияние комплекса систематических факторов и после исключения этого влияния из фактических уровней в них остаются значения, случайные по своей природе. Поэтому нет формальных ограничений на использование степенной модели в прогнозных расчётах.
5.Выполним расчёт параметров уравнения параболы второго порядка и оценим возможность её использования для выполнения прогнозов.
Значения параметров рассчитаем, используя определители третьего порядка, формулы которых приведены в решении типовой задачи №1. Необходимые данные представлены в табл. 8. В результате получены следующие значения определителей системы нормальных уравнений:
Таблица 8
| Годы | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 75,3 | 75,3 | 75,3 | 75,9 | -0,6 | 0,36 | 0,9 | |||||
| 73,8 | 147,6 | 295,2 | 73,7 | 0,1 | 0,01 | 0,1 | |||||
| 72,1 | 216,3 | 648,9 | 71,7 | 0,4 | 0,16 | 0,6 | |||||
| 70,9 | 283,6 | 1134,4 | 69,9 | 1,0 | 1,00 | 1,4 | |||||
| 68,5 | 342,5 | 1712,5 | 68,4 | 0,1 | 0,01 | 0,2 | |||||
| 66,4 | 398,4 | 2390,4 | 67,0 | -0,6 | 0,36 | 0,9 | |||||
| 66,0 | 462,0 | 65,9 | 0,1 | 0,01 | 0,1 | ||||||
| 64,7 | 517,6 | 4140,8 | 65,1 | -0,4 | 0,16 | 0,5 | |||||
| 63,8 | 574,2 | 5167,8 | 64,4 | -0,6 | 0,36 | 0,9 | |||||
| 64,0 | 640,0 | 64,0 | 0,0 | 0,00 | 0,0 | ||||||
| 64,3 | 707,3 | 7780,3 | 63,8 | 0,5 | 0,25 | 0,8 | |||||
| Итого | 749,8 | 4364,8 | 32979,6 | 749,8 | 0,0 | 2,68 | 6,5 | ||||
| Средняя | 68,2 | — | — | — | — | — | — | — | 0,24 | 0,6 | |
| Сигма | 4,01 | 3,16 | — | — | — | — | — | — | — | — | — |
| D | 16,08 | 10,0 | — | — | — | — | — | — | — | — | — |






