Значения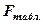 
представлены в таблице «Значения F -критерия Фишера». (См. приложение 1 данных «Методических указаний…»).
В рассматриваемой задаче 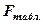для 
и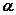 
=0,05 соствляет 3,88. В силу того, что 
нулевую гипотезу о статистической незначимости характеристик уравнения №1 следует отклонить, то есть 
. Аналогичное решение принимается и относительно второй нулевой гипотезы, т.к. 
. То есть,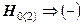 
.Отклоняя нулевую гипотезу, допустимо (с определённой степенью условности) принять одну из альтернативных гипотез. В частности, может быть рассмотрена и принята гипотеза о том, что параметры моделей неслучайны, то есть формируются под воздействиемпредставленных в моделях факторов, влияние которых на результат носит систематический, устойчивый характер. Это означает, что полученные результаты могут быть использованы в аналитической работе и в прогнозных расчётах среднемесячной заработной платы и стоимости валового регионального продукта, которые основаны не только на влиянии 
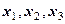, но и на влиянии эндогенной переменной 
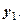Рекурсивные модели связей предоставляют возможность подобного анализа и прогноза.
Задача №4.
Предлагается изучить взаимосвязи социально-экономических характеристик региона за период.
Y1 - инвестиции текущего года в экономику региона, млрд. руб.
Y2 - стоимость продукции промышленности и АПК в текущем году, млрд. руб.
Y3 - оборот розничной торговли в текущем году, млрд. руб.
х1 - инвестиции прошлого года в экономику региона, млрд. руб.
х2 - среднегодовая стоимость основных фондов в экономике региона, млрд. руб.
х3 - среднегодовая численность занятых в экономике региона, млн. чел.
Приводится система рабочих гипотез, которые необходимо проверить.
Задание
1. Используя рабочие гипотезы, постройте систему уравнений, определите их вид и проведите их идентификацию.
2. Укажите, при каких условиях может быть найдено решение каждого из уравнений и системы в целом. Дайте обоснование возможных вариантов подобных решений и аргументируйте выбор оптимального варианта рабочих гипотез.
3. Опишите методы, с помощью которых будет найдено решение уравнений (косвенный МНК, двухшаговый МНК).
Решение.
1. В соответствии с предложенными рабочими гипотезами построим график, отображающий связи каждой из представленных переменных с другими переменными. См. рис. 2. Отличительной особенностью уравнений системы является наличие прямых и обратных зависимостей между переменными Y1, Y2 и Y3. Указанная особенность характерна для так называемых структурных уравнений. В состав структурных уравнений входят: а ) эндогенные переменные (Yj), значения которых формируется в условиях данной системы признаков и их взаимозависимостей и б) экзогенные переменные (xm), значения которых формируются вне данной системы признаков и условий, но сами экзогенные переменные участвуют во взаимосвязях данной системы и оказывают влияние на эндогенные переменные. Коэффициенты при эндогенных переменных обозначаются через 
, коэффициенты при экзогенных переменных обозначаются через 
, где i- число изучаемых объектов; m –число экзогенных переменных, которые обычно обозначают через x; j - число эндогенных переменных, обычно обозначаемых через Y. Таким образом, в каждом уравнении системы каждый коэффициент при переменной имеет двойную индексацию: 1) - номер эндогенной переменной, расположенной в левой части уравнения и выступающей в качестве результата; 2) – номер переменной, находящейся в правой части уравнения и выступающей в качестве фактора.
В нашей задаче система уравнений для описания выдвигаемые рабочие гипотезы будет иметь следующий вид:
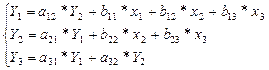
2. Выполним идентификацию каждого структурного уравнения и всей системы для ответа на вопрос – имеют ли решения каждое из уравнений и система в целом. Воспользуемся счётным правилом, по которому в каждом уравнении системы необходимо сравнить число эндогенных переменных в данном уравнении – Y H и число отсутствующих в уравнении экзогенных переменных из общего для всей системы их перечня – 
. Для удобства анализа представим результаты в таблице.
Результаты идентификации структурных уравнений и всей системы.
| Номер уравнения | Число эндогенных переменных в уравнении, H | Число экзогенных переменных из общего их списка, отсутствующих в уравнении, D | Сравнение параметров H и D+1 | Решение об идентификации уравнения |
| 2 > 0+1 | Неидентифицировано | |||
| 2 = 1+1 | Точно идентифицировано | |||
| 3 < 3+1 | Сверхидентифицировано | |||
| Вся система уравнений в целом | Неидентифицирована |
3. В том случае, когда хотя бы одно из уравнений не имеет решения, система в целом также не имеет решения. Если подобный результат нас не устраивает, необходимо внести коррективы в исходные рабочие гипотезы и отредактировать их таким образом, чтобы идентификация была возможна.
4. Теоретический анализ содержания взаимосвязи, отражённой в уравнении №1, позволяет рассмотреть варианты возможной корректировки. Во-первых, из правой части может быть исключёна одна из экзогенных переменных. Скорее всего, ею может оказаться x3 – среднегодовая численность занятых в экономике региона, (млн. чел.), так как по своему экономическому смыслу она менее тесно связана с инвестициями, чем инвестиции прошлого года (
) и среднегодовая стоимость основных фондов в экономике региона, (
).
Во-вторых, возможна корректировка путём исключения из правой части уравнения эндогенной переменной Y2 - стоимость продукции промышленности и АПК в текущем году, млрд. руб. Но в этом случае, уравнение перестанет быть структурным, следовательно, изучить обратную связь Y1 и Y2 будет невозможно. По этой причине подобная корректировка является нецелесообразной.
При корректировке рабочей гипотезы путём удаления x3 уравнение №1 становится точно идентифицированным, а вся система – сверхидентифицированной.
5. Для поиска решений сверхидентифицированной системы уравнений применяются: а) косвенный метод наименьших квадратов (КМНК) для решения точно идентифицированных уравнений и б) двухшаговый МНК (ДМНК) для поиска решений сверхидентифицированных уравнений.
Задача №5.
По территориям Центрального федерального округа России имеются данные за 2000 год о следующих показателях:
Y1 – валовой региональный продукт, млрд. руб.
Y2 - розничный товарооборот, млрд. руб.
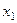- основные фонды в экономике, млрд. руб.
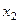- инвестиции в основной капитал, млрд. руб.
- численность занятых в экономике, млн. чел.
- среднедушевые расходы населения за месяц, тыс. руб.
Изучения связи социально-экономических показателей предполагает проверку следующих рабочих гипотез:
Для их проверки выполнена обработка фактических данных и получена следующая система приведённых уравнений:
Задание:
1. Построить систему структурных уравнений и провести её идентификацию;
2. Проанализировать результаты решения приведённых уравнений;
3. Используя результаты построения приведённых уравнений, рассчитать параметры структурных уравнений (косвенный МНК); проанализировать результаты;
4. Указать, каким образом можно применить полученные результаты для прогнозирования эндогенных переменных 
и 
Решение.
1. Построение системы структурных уравнений выполняется в соответствии с рабочими гипотезами:
2. В соответствии со счётным правилом оба уравнения и система в целом являются точно идентифицированными и это означает, что они имеют единственное решение, которое может быть получено косвенным МНК (КМНК).
| Номер уравнения | Число эндогенных переменных в уравнении, H | Число экзогенных переменных из общего их списка, отсутствующих в уравнении, D | Сравнение параметров H и D+1 | Решение об идентификации уравнения |
| 2 = 1+1 | точно идентифицировано | |||
| 2 = 1+1 | точно идентифицировано | |||
| Система уравнений в целом | точно идентифицирована |
3. Процедура КМНК состоит в том, чтобы путём преобразования результатов решения приведённых уравнений получить искомые структурные уравнения. Используемый приём подстановок обеспечивает получение точных результатов только в том случае, если выполняемые преобразования точны и безошибочны. Чтобы получить первое структурное уравнение из первого приведённого необходимо отсутствующий в структурном уравнении признак выразить через Y2, используя результаты второго приведённого уравнения. То есть:
После подстановки значения в первое приведённое уравнение и преобразования подобных членов, получаем следующий результат:
.
Как видим, полученный результат соответствует исходной рабочей гипотезе. Анализ показывает, что стоимость ВРП находится в прямой зависимости от розничного товарооборота, стоимости основных фондов в экономике, от размера инвестиций в экономику и от численности населения, занятого в экономике региона.Указанные переменные объясняют 86,3% вариации результата, а характеристики установленной зависимости являются статистически значимыми и надёжными, так как
для 
.
Следовательно, есть основания для отклонения нулевой гипотезы о случайной природе выявленной зависимости.
Аналогично выполняем преобразования для определения параметров второго структурного уравнения. Выразим отсутствующий в уравнении 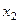через Y1, используя результаты построения первого приведённого уравнения. То есть:
.
После подстановки значения 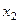во второе приведённое уравнение и преобразования подобных членов получаем следующий результат:
.
Уравнение описывает линейную зависимость розничного товарооборота от стоимости ВРП, основных фондов в экономике, от численности занятых в экономике и от уровня среднедушевых расходов населения за месяц. Данный перечень переменных объясняет 87,4% вариации оборота розничной торговли, а соотношение позволяет отклонить нулевую гипотезу о случайной природе выявленной зависимости.
4. Для выполнения прогнозных расчётов 
и 
наиболее простым является вариант, по которому прогнозные значения экзогенных переменных (
) подставляются в приведённые уравнения. Точность и надёжность прогнозов в этом случае зависит от качества приведённых моделей и от того, как сильно отличаются прогнозные значения экзогенных переменных от их средних значений.
Задача №6.
Среднегодовая численность занятых в экономике Российской Федерации, млн. чел., за период с 1990 по 2000 год характеризуется следующими данными:
| Годы | Qt | Годы | Qt |
| 75,3 | 66,4 | ||
| 73,8 | 66,0 | ||
| 72,1 | 64,7 | ||
| 70,9 | 63,8 | ||
| 68,5 | 64,0 | ||
| 64,3 |
Задание:
1. Постройте график фактических уровней динамического ряда -Qt
2. Рассчитайте параметры параболы второго порядка: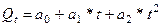 
,
линейной: 
и логарифмической функций: 
3. Оцените полученные результаты:
- с помощью показателей тесноты связи (ρ и ρ2 );
- значимость модели тренда (F- критерий);
- качество модели через корректированную среднюю ошибку аппроксимации 
, а также через коэффициент автокорреляции отклонений от тренда - 
4. Выберите лучшую форму тренда и выполните по ней прогноз до 2003 года.
5. Проанализируйте полученные результаты.
Решение:
1. Общее представление о форме основной тенденции в уровнях ряда даёт график их фактических значений. Для его построения введём дополнительные обозначения для комплекса систематически действующих факторов, который по традиции обозначим через t и условно отождествим с течением времени. Для обозначения комплекса систематических факторов используются числа натурального ряда: 1, 2, 3, …, n. См. табл. 1.
В первую очередь выявим линейный тренд и проверим его статистическую надёжность и качество. Параметры рассчитаем с помощью определителей второго порядка, используя формулы, рассмотренные нами в зад. 1. Получены значения определителей: 
; 
; 
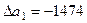. С их помощью получены следующие параметры линейного тренда: 
; 
, уравнение имеет вид: 
. Уравнение детерминирует 92,2% вариации численности занятых (
; 
).
Таблица 1.
| Годы | Qt | T | t2 | Qt*t | Qt расч. | DQt | (dQt)2 | 
|
| А | ||||||||
| 75,3 | 75,3 | 74,3 | 1,0 | 1,0 | 1,5 | |||
| 73,8 | 147,6 | 73,0 | 0,8 | 0,6 | 1,1 | |||
| 72,1 | 216,3 | 71,8 | 0,3 | 0,1 | 0,4 | |||
| 70,9 | 283,6 | 70,6 | 0,3 | 0,1 | 0,4 | |||
| 68,5 | 342,5 | 69,4 | -0,9 | 0,8 | 1,3 | |||
| 66,4 | 398,4 | 68,2 | -1,8 | 3,2 | 2,6 | |||
| 66,0 | 462,0 | 66,9 | -0,9 | 0,8 | 1,4 | |||
| 64,7 | 517,6 | 65,7 | -1,0 | 1,0 | 1,5 | |||
| 63,8 | 574,2 | 64,5 | -0,7 | 0,5 | 1,0 | |||
| 64,0 | 640,0 | 63,3 | 0,7 | 0,5 | 1,0 | |||
| 64,3 | 707,3 | 62,1 | 2,2 | 4,8 | 3,3 | |||
| Итого | 749,8 | 4364,8 | 749,8 | 0,0 | 13,4 | 15,6 | ||
| Средняя | 68,2 | 6,0 | — | — | — | — | — | 1,4 |
| Сигма | 4,01 | 3,16 | — | — | — | — | — | — |
| Дисперсия, D | 16,08 | 10,0 | — | — | — | — | — | — |
Средняя ошибка аппроксимации 
очень невелика ( = 1,4%), что указывает на высокое качество модели тренда и возможность её использования для решения прогнозных задач. Фактическое значение F -критерия составило 108 и сравнение с 5,12 его табличного значения позволяет сделать вывод о высокой степени надёжности уравнения тренда.
Для дополнительной проверки качества тренда выполним расчёт коэффициента корреляции отклонений фактических уровней от рассчитанных по уравнению тренда. Если будет установлено отсутствие связи отклонений, это укажет на их случайную природу, то есть на то, что тренд выбран верно, что он полностью исключил основную тенденцию из фактических уровней ряда и что он сформировал случайный значения отклонений.
 |
Выполним расчёт в табл.2. Поместим во второй графе фактические отклонения от тренда 
, для удобства расчёта обозначим их через Y. В соседней графе поместим эти же отклонения, но, сместив их относительно первой строки на один год вниз; обозначим их через 
и рассмотрим в качестве фактора X. Линейный коэффициент корреляции отклонений рассчитаем по формуле: 
Используем значения определителей второго порядка для расчёта коэффициента регрессии с1, который отражает силу связи отклонений и . Получены следующие значения определителей:
Отсюда 
. При этом, коэффициент корреляции отклонений составит:
В данном случае выявлена заметная связь, существенность которой подтверждает сравнение фактического и табличного значений F - критерия: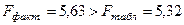 
. Следовательно, нулевая гипотеза о случайной природе отклонений не может быть принята, отклонения связаны между собой и не являются случайными величинами. То есть, линейный тренд не полностью исключил из фактических уровней влияние систематических факторов, формирующих основную тенденцию. Следует рассмотреть тренд иной формы.
Таблица 2
| (Y)
| (X)
| 
| 
| |
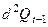
| 1,0 | — | — | — | |
| 0,8 | 1,0 | 0,8 | 1,0 | |
| 0,3 | 0,8 | 0,2 | 0,6 | |
| 0,3 | 0,3 | 0,1 | 0,1 | |
| -0,9 | 0,3 | -0,3 | 0,1 | |
| -1,8 | -0,9 | 1,6 | 0,8 | |
| -0,9 | -1,8 | 1,6 | 3,2 | |
| -1,0 | -0,9 | 0,9 | 0,8 | |
| -0,7 | -1,0 | 0,7 | 1,0 | |
| 0,7 | -0,7 | -0,5 | 0,5 | |
| 2,2 | 0,7 | 1,5 | 0,5 | |
| Итого | -1,0 | -2,2 | 6,6 | 8,6 |
| Средняя | -0,1 | -0,2 | — | — |
| Сигма | 1,12 | 0,91 | — | — |
2. Рассмотрим возможность использования для описания тренда равносторонней гиперболы: 
. В качестве аргумента в уравнении тренда здесь выступает 
. Выполним расчёт параметров и оценим полученное уравнение. См. табл. 3.
Таблица 3
| Годы | 
|
| 
| 
|  .
|
| 
|
|
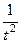
| 75,3 | 1,000 | 75,300 | 1,0000 | 77,8 | -2,5 | 6,3 | 3,7 | |
| 73,8 | 0,500 | 36,900 | 0,2500 | 71,2 | 2,6 | 6,8 | 3,9 | |
| 72,1 | 0,333 | 24,033 | 0,1111 | 68,9 | 3,2 | 10,2 | 4,6 | |
| 70,9 | 0,250 | 17,725 | 0,0625 | 67,8 | 3,1 | 9,6 | 4,5 | |
| 68,5 | 0,200 | 13,700 | 0,0400 | 67,2 | 1,3 | 1,7 | 2,0 | |
| 66,4 | 0,167 | 11,067 | 0,0278 | 66,7 | -0,3 | 0,1 | 0,5 | |
| 66,0 | 0,143 | 9,429 | 0,0204 | 66,4 | -0,4 | 0,2 | 0,6 | |
| 64,7 | 0,125 | 8,088 | 0,0156 | 66,2 | -1,5 | 2,2 | 2,2 | |
| 63,8 | 0,111 | 7,089 | 0,0123 | 66,0 | -2,2 | 4,8 | 3,2 | |
| 64,0 | 0,100 | 6,400 | 0,0100 | 65,8 | -1,8 | 3,2 | 2,7 | |
| 64,3 | 0,091 | 5,845 | 0,0083 | 65,7 | -1,4 | 2,0 | 2,1 | |
| Итого | 749,8 | 3,020 | 215,575 | 1,5580 | 749,8 | 0,0 | 47,1 | 29,9 |
| Средняя | 68,16 | 0,275 | — | — | — | — | 4,3 | 2,7 |
| Сигма | 4,01 | 0,257 | — | — | — | — | — | — |
| D | 16,08 | 0,066 | — | — | — | — | — | — |
