На выбор потребителя оказывают влияние две группы факторов: предпочтения и ограничения. Предпочтение – это признание того, что некоторое благо или набор благ является для человека более полезным, чем другое благо или набор благ.
В экономической теории в отношении потребительских предпочтений используются следующие предпосылки или аксиомы:
1. Аксиома полноты или упорядоченности. В соответствии с ней предполагается, что потребитель способен упорядочить любые комбинации (наборы) благ в соответствии со своими предпочтениями. Это означает, что потребитель может сравнить два набора благ и сказать, какой из них является более предпочтительным или они являются для него равноценными (отношения предпочтения записываются так: A > B; отношения безразличия: A ~ B).
2. Аксиома транзитивности. В соответствии с ней предполагается, что, если некоторый набор благ А предпочитается набору В, а набор В в свою очередь предпочитается набору С, то А предпочитается С (записывается это так: если А > В, а В > С, то А > С); или: если А ~ В, а В > C, то A > C; или: если A > B, а B ~ C, то A > C).
3. Аксиома ненасыщения. Предполагается, что потребитель всегда предпочтет большее количество блага меньшему: если набор А содержит какого-то товара на единицу больше, чем набор В, то
А > В.
Графически потребительские предпочтения анализируются с помощью кривых безразличия. Кривая безразличия – это кривая, представляющая собой геометрическое место точек сочетания двух благ (X и Y), которые обеспечивают одинаковый уровень полезности и поэтому равноценны (безразличны) для потребителя (рис. 4.1).
Совокупность кривых безразличия, отражающих разный уровень полезности двух благ для отдельного потребителя, образуют карту безразличия (рис. 4.2). Каждая кривая на этой карте показывает набор товаров, к которым потребитель относится одинаково, т. е. безразлично.
| Рис. 4.1. Кривая
безразличия
|
| Рис. 4.2. Карта
безразличия
|
Кривые безразличия обладают следующими свойствами:
1.Кривые безразличия выпуклы к началу координат. Это свойство обусловливается убыванием предельной нормы замещения. Предельная норма замещения (MRS) – это количество одного товара (Y), от которого готов отказаться потребитель, чтобы получить дополнительную единицу другого товара (X), оставаясь при этом на том же уровне полезности:
 .
.
Двигаясь по кривой безразличия сверху вниз, потребитель наращивает потребление товара X, отказываясь при этом от потребления все меньшего количества товара Y. Это означает, что по мере увеличения потребления одного товара, норма замещения уменьшается. Поэтому кривые безразличия выпуклы к началу координат.
Выпуклость кривой безразличия имеет два крайних случая (исключения):
а) если два блага являются абсолютными субститутами, то кривая безразличия принимает вид прямой линии, а  – величина постоянная (рис. 4.3, а);
– величина постоянная (рис. 4.3, а);
б) если два блага абсолютно комплементарны, то кривая безразличия принимает вид взаимно перпендикулярных отрезков (рис. 4.3, б). MRS в данном случае стремится к бесконечности на вертикальном участке кривой безразличия и равна нулю на горизонтальной оси (в угловой точке – не определена).
| Рис. 4.3. Кривые безразличия: а – для абсолютных субститутов;
б – для абсолютных комплементов.
|
2. Более высокие кривые безразличия соответствуют более высоким уровням полезности. Это означает, что кривая безразличия, лежащая выше и правее другой кривой безразличия, выражает более предпочтительный для данного потребителя набор товаров. Это свойство кривых безразличия вытекает из аксиом ненасыщения и транзитивности.
Рассмотрим две кривые безразличия ( и
и  ) с наборами благ А, В и С (рис. 4.4).При этом наборы А и В, как принадлежащие одной кривой безразличия, равноценны для потребителя: А ~ В. Набор С содержит такое же количество блага Y, что и набор А, но большее количество блага X. Поэтому в соответствии с аксиомой ненасыщения С > А. Из аксиомы транзитивности в свою очередь следует, что поскольку С > А,а А ~ В,то С > В. Обобщая, получим, что все наборы благ, принадлежащие кривой безразличия
) с наборами благ А, В и С (рис. 4.4).При этом наборы А и В, как принадлежащие одной кривой безразличия, равноценны для потребителя: А ~ В. Набор С содержит такое же количество блага Y, что и набор А, но большее количество блага X. Поэтому в соответствии с аксиомой ненасыщения С > А. Из аксиомы транзитивности в свою очередь следует, что поскольку С > А,а А ~ В,то С > В. Обобщая, получим, что все наборы благ, принадлежащие кривой безразличия 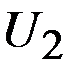 , более предпочтительны всех наборов, принадлежащих кривой безразличия
, более предпочтительны всех наборов, принадлежащих кривой безразличия 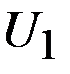 .
.
| Рис. 4.4. Кривые безразличия
|
3. Кривые безразличия имеют отрицательный наклон. Положительный наклон кривых безразличия невозможен, так как это противоречит аксиоме ненасыщения.
Пусть дана кривая безразличия U с набором благ А, В, С
(рис. 4.5). Проведем через точку В две взаимно перпендикулярные прямые. Мы получим 4 квадранта. При этом кривые безразличия с отрицательным наклоном будут принадлежать II и IV квадрантам, а с положительным – I и III квадрантам. Все точки, лежащие в III квадранте, содержат б о льшее, а все точки, лежащие в I квадранте, – м е ньшее количество благ X и Y,чем точка В. Соответственно, точки, лежащие в III квадранте, более предпочтительны, а лежащие в
I квадранте – менее предпочтительны, чем точка В (аксиома ненасыщения). Следовательно, точки, безразличные В, например точки А и С, должны находиться либо во II, либо в IV квадранте, а значит, кривая безразличия должна иметь отрицательный наклон.
| Рис. 4.5. Кривая безразличия имеет отрицательный наклон
|
4. Кривые безразличия никогда не пересекаются. Для доказательства этого свойства предположим, что кривые безразличия ( и
и  ) пересекаются в точке А (рис. 4.6).
) пересекаются в точке А (рис. 4.6).
| Рис. 4.6. Невозможность пересечения кривых безразличия
|
Из аксиомы о ненасыщении следует, что В > С (В содержит больше Y,чем С). Наборы А и С лежат на одной кривой безразличия  , поэтому А ~ С. Наборы А и В лежат на одной кривой безразличия
, поэтому А ~ С. Наборы А и В лежат на одной кривой безразличия  , и поэтому А ~ В. Из аксиомы о транзитивности следует, что если А ~ С и А ~ В, то В ~ С. Однако не могут одновременно быть В > С и В ~ С. Следовательно, кривые безразличия не могут пересекаться.
, и поэтому А ~ В. Из аксиомы о транзитивности следует, что если А ~ С и А ~ В, то В ~ С. Однако не могут одновременно быть В > С и В ~ С. Следовательно, кривые безразличия не могут пересекаться.
 .
. – величина постоянная (рис. 4.3, а);
– величина постоянная (рис. 4.3, а); и
и  ) с наборами благ А, В и С (рис. 4.4).При этом наборы А и В, как принадлежащие одной кривой безразличия, равноценны для потребителя: А ~ В. Набор С содержит такое же количество блага Y, что и набор А, но большее количество блага X. Поэтому в соответствии с аксиомой ненасыщения С > А. Из аксиомы транзитивности в свою очередь следует, что поскольку С > А,а А ~ В,то С > В. Обобщая, получим, что все наборы благ, принадлежащие кривой безразличия
) с наборами благ А, В и С (рис. 4.4).При этом наборы А и В, как принадлежащие одной кривой безразличия, равноценны для потребителя: А ~ В. Набор С содержит такое же количество блага Y, что и набор А, но большее количество блага X. Поэтому в соответствии с аксиомой ненасыщения С > А. Из аксиомы транзитивности в свою очередь следует, что поскольку С > А,а А ~ В,то С > В. Обобщая, получим, что все наборы благ, принадлежащие кривой безразличия 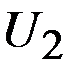 , более предпочтительны всех наборов, принадлежащих кривой безразличия
, более предпочтительны всех наборов, принадлежащих кривой безразличия 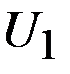 .
. и
и  ) пересекаются в точке А (рис. 4.6).
) пересекаются в точке А (рис. 4.6).

 , поэтому А ~ С. Наборы А и В лежат на одной кривой безразличия
, поэтому А ~ С. Наборы А и В лежат на одной кривой безразличия  , и поэтому А ~ В. Из аксиомы о транзитивности следует, что если А ~ С и А ~ В, то В ~ С. Однако не могут одновременно быть В > С и В ~ С. Следовательно, кривые безразличия не могут пересекаться.
, и поэтому А ~ В. Из аксиомы о транзитивности следует, что если А ~ С и А ~ В, то В ~ С. Однако не могут одновременно быть В > С и В ~ С. Следовательно, кривые безразличия не могут пересекаться.





