Метод основан на графическом определении отрезков времени Dt по отрезкам Dw, которыми последовательно и произвольно задаются. Для малых конечных приращений Dt и Dw уравнение движения электропривода запишется следующим образом:
, (8.1)
где МСР и МС.СР – средние значения момента двигателя и момента статического сопротивления для соответствующих нелинейных характеристик на участке Dw приращения скорости.
Для графического интегрирования уравнение (8.1) запишется в виде следующей пропорции (отсюда и название метода):
, (8.2)
где mM, mJ, mw, mt – масштабные коэффициенты соответствующих фазовых координат и времени.
Эта пропорция (8.2) показывает действительное соотношение величин, входящих в уравнение движения, если будет выдержано условие:
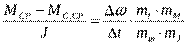(8.3)
при
. (8.4)
Обычно три масштабных коэффициента (mM, mw и mt) выбирают по масштабам заданных механических характеристик двигателя w=f(M) и рабочей машины МС=f(w), а также по желаемому представлению рассчитываемой кривой w=f(t). Четвертый же масштабный коэффициент (mJ) рассчитывают из условия (8.4), а именно:
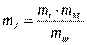. (8.5)
Рассмотрим применение графического метода пропорций на примере расчета переходного процесса пуска электропривода вентилятора с асинхронным короткозамкнутым двигателем.
Н 
а рисунке 8.1 приведены заданные механические характеристики двигателя (кривая 1) и вентилятора (кривая 2). Вычитая при одной и той же скорости МС из М, можно получить кривую динамического момента Мj=М-МС (кривая 3). Затем кривая Мj=f(w) аппроксимируется прямоугольными участками, как это показано на рисунке 8.1. Чем больше участков аппроксимации, тем точнее будет графическое построение кривой w=f(t). На рисунке 8.1 для упрощения кривая динамического момента аппроксимирована 6-ю участками.
Рассмотрим последовательность графического интегрирования уравнения движения и доказательство справедливости такого решения.
На оси моментов откладываем в масштабе mJ отрезок 
, пропорциональный моменту инерции J электропривода, предварительно выбрав масштаб mt по условиям получения кривой w=f(t) на заданном участке площади рисунка.
Затем переносим на ось ординат отрезок ОВ (точка 1), равный динамическому моменту Мj1, отрезки 02, 03, …, 06, равные динамическим моментам Мj2, Мj3, …, Мj6. Из точки О проводим луч 
до пересечения с линией окончания первого участка аппроксимации кривой динамического момента.
Затем из точки К проводим луч 
и т.д. Соединяя точки О, К, N и т.д., получаем кусочно-линейную функцию w(t), являющуюся графиком механического переходного процесса при пуске двигателя.
Докажем справедливость построения функции w(t).
Так как D ОКС ¥D РВО (по построению), то
. Так как 
, 
, 
, 
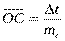, то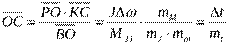 
.
Отсюда следует, что 
.
Таким образом, построение выполнено верно, если масштабные коэффициенты будут выбраны так, чтобы удовлетворять условию:.
Точность графического решения определяется выбранными масштабами и числом участков прямоугольной аппроксимации кривой динамического момента.
М 
етод пропорций можно применить и для построения графика w=f(t) при торможении привода, как это показано на рисунке 8.2. Построения понятны из рисунка и не требуют пояснений, если учесть, что динамический момент в этом случае вычисляется по соотношению: Мj=МСР+МС.СР, а для торможения механизма используется режим противовключения с соответствующей механической характеристикой М=f(w).
