Состояние идеального газа. Частицы (атомы, молекулы) реально существующих газов обладают собственными размерами, занимают некоторый объем пространства, и в некоторой степени зависимы друг от друга. Силы физического взаимодействия между частицами газа затрудняют их движение и уменьшают их подвижность. По этим причинам газовые законы и следствия из них достаточно строго соблюдаются только для разреженных реальных газов, для которых рассояние между частицами значительно превышает собственный размер частиц газа, а взаимодействие между частицами сведено к минимуму. При обычном (атмосферном) давлении газовые законы становятся приблеженными, а при высоком давлении не выполняются совсем.
В связи с этим в науке присутствует понятие о состоянии идеального газа, при котором частицы рассматриваются как геометрические точки с нулевыми размерами и не взаимодействующие друг с другом. Таким образом, идеальный газ - это абстракция, а реальный газ приближается к модели идеального газа тем в большей степени, чем больше различаются температура равновесной конденсации этого газа и температура, при которой этот газ находится.
При комнатной температуре и атмосферном давлении к идеальному состоянию приближаются такие газы, как H2, N2, O2, температуры равновесной конденсации которых равны (округленно) 20K, 77K, 90K. Аммиак и диоксид серы (температура конденсации 240K 263K) далеки от состояния идеального газа, но при 500°C и выше поведение этих газов уже подчиняется, приближенно, уравнению состояния идеального газа.
Уравнение состояния идеального газа. Значение молярного объема газа, равное 22,4 л/моль, относится к норамльным физическим условиям, под которыми понимаются давление равное 1,01325·105 Па, или 1 атм, и термодинамическая температура, равная 273,15 К (0°C).
Между значениями термодинамической температуры T, выраженной в кельвинах K (не правильно использовать гибридное обозначение кельвина как °K, это запрещено в Международной системе единиц), и температуры Цельсия, выраженной в градусах Цельсия (обозначение °C) существует простая зависимость:
| T(K) | = | t(°C) + 273.15 |
В практических расчетах разность (T - t) можно считать равной 273.
В химических реакциях указанные выше нормальные условия практически не реализуются. Поэтому, прежде чем проводить какие либо расчеты или сопоставления, измеренные при некоторых других условиях объемы газов необходимо пересчитывать применительно к нормальным условиям.
Для приведения объема газа к нормальным условиям можно пользоваться уравнением объединенного газоваго закона, выведенным французским физиком Клапейроном и носящим его имя:
| pV | = | const | или | pV | = | p0V0 |
| ----- | ----- | ----- | ||||
| T | T | T0 |
где
p (кПа), V (см3, дм3, м3), T (K) - параметры некоторого состояния идеального газа (отличные от н.у.);
p0, V0, T0 - параметры, отвечающие нормальным условиям.
Из последнего уравнения можно рассчитать значение V0 (объем газа при н.у.), если измерен объем V газа при некоторых других условиях:
| V0 | = | pVT0 |
| ------- | ||
| p0T |
Также легко пересчитать значение V0 на условия эксперимента:
| V | = | p0V0T |
| ------- | ||
| pT0 |
Соотношение pV/T является постоянной величиной при любых заданных значениях p и V для любого измеренного объема идеального газа, следовательно, оно постоянно и для молярного объема идеального газа и при нормальных условиях:
| R | = | p0VM | = | 101.325 (кПа) · 22,41383 (л/моль) | = | 8,31441 | кПа · л | |
| ------- | ---------------------------------------- | --------- | ||||||
| T0 | 100 (кПа) · 273 (K) | моль · K |
Поскольку произведение объема на давление есть энергия W = pV, то и произведение единиц объема (м3) и давления (Па) есть единица энергии - джоуль в СИ (Дж). Следовательно, значение постоянной R в системе СИ составит:
| R | = | 8.31441 Дж/(моль·K) |
Таким образом, для 1 моль идеального газа и, следовательно, всех реальных газов, по свойствам приближающихся к идеальной модели, при нормальных условиях значение R называется универсальной газовой постоянной.
Соотношение между параметрами идеального газа (давлением p, объемом V, количеством вещества n, термодинамической температурой T) описывает уравнение Клапейрона-Менделеева:
| pV | = | nRT |
Уравнение Клапейрона-Менделеева устанавливает связь между давлением, объемом и температурой любой порции газа со свойствами идеальной модели, поэтому называется уравнение состояния идеального газа.
Уравнение состояния идеального газа, позволяет проводить расчеты параметров реальных газов при физических условиях, приближающихся к нормальным условиям.
12) Реальные газы. Уравнение процесса с реальными газами.
РЕА́ЛЬНЫЙ ГАЗ, газ, свойства которого существенно зависят от взаимодействия молекул (см. Межмолекулярное взаимодействие).
В обычных условиях, когда средняя потенциальная энергия взаимодействия молекул много меньше их средней кинетической энергии, свойства реальных газов незначительно отличаются от свойств идеального газа и к реальным газам применимы законы, установленные для идеального газа. Отличие свойств реального газа от свойств идеального становится особенно значительным при высоких давлениях и низких температурах, когда начинают проявляться квантовые эффекты.
В модели идеального газа не учитывается собственный объем молекул и силы межмолекулярного взаимодействия. Тщательная экспериментальная проверка газовых законов (закон Бойля —Мариотта, закон Шарля, закон Гей-Люссака) современными методами показала, что эти законы достаточно точно описывают поведение реальных газов при небольших давлениях и высоких температурах. При других условиях наблюдаются значительные отступления от этих законов. Причина заключается в том, что, во-первых, при очень сильном сжатии газов объем незанятого молекулами пространства становится сравним с объемом, занимаемым самими молекулами; а во-вторых, при низких температурах становится заметным взаимодействие между молекулами. Поэтому для описания поведения газа при достаточно больших плотностях (больших давлениях) уравнения состояния идеального газа не пригодны. Наличие сил межмолекулярного взаимодействия, а именно сил отталкивания, действующих на малых расстояниях порядка размеров молекул, и сил притяжения, приводит к сложной зависимости энергии потенциального взаимодействия молекул от расстояния.
Для описания термодинамических свойств реальных газов используются различныеуравнения состояния. При малых плотностях наличие межмолекулярного взаимодействия учитывается вириальным уравнением состояния реального газа:
pV = RT[1 + B(T)/v + C(T)/v2+...],
где p — давление, v — мольный объем, Т — абсолютная температура, R — газовая постоянная, В(Т), С(Т) и т. д. — вириальные коэффициенты, зависящие от температуры и характеризующие парные, тройные и т. д. взаимодействия частиц в газе. Качественно верно описывает основные отличия реального газа от идеального уравнение Ван-дер-Ваальса, учитывающее существование сил притяжения между молекулами, действие которых приводит к уменьшению давления газа, и сил отталкивания, препятствующих безграничному сжатию газа.
Кроме уравнения Ван-дер-Ваальса было предложено много других эмпирических уравнений состояния реальных газов. Некоторые из них дают лучшее согласие с опытом за счет большого числа входящих в них феноменологических постоянных. Однако при качественном исследовании поведения реальных газов использование уравнения Ван-дер-Ваальса более удобно, благодаря его простоте и понятному физическому смыслу.
Одной из основных характеристик реальных газов являются размеры молекул. В реальных газах их называют газокинетическими радиусами, и их размер связан с характерными расстояниями, на которых проявляются силы межатомных и межмолекулярных взаимодействий.В реальных газах возникают неоднородности полей давления и температуры, а также макроскопические потоки, которые приводят к переносу массы — диффузии. Для реальных газов характерна теплопроводность и вязкость. Главная особенность кинетических процессов переноса в реальных газах (в отличие от жидкостей и твердых тел) — наличие механизма столкновения молекул. Поэтому основной характеристикой этих процессов в газах является длина свободного пробега.Внутренняя энергия реального газа зависит от объема V, то есть от расстояния между молекулами, так как потенциальная энергия молекул определяется их взаимным расположением.
Существование межмолекулярного взаимодействия в той или иной степени сказывается на всех свойствах реальных газов.
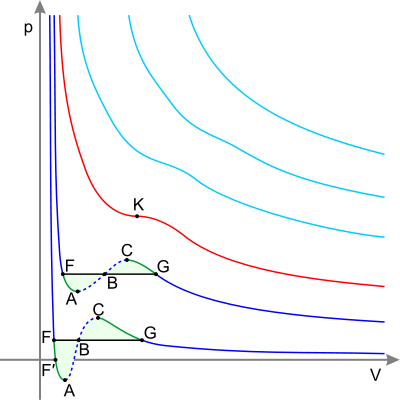

Изотермы реального газа (схематично)
Синие — изотермы при температуре ниже критической. Зелёные участки на них — метастабильные состояния.
Участок левее точки F — нормальная жидкость.
Точка F — точка кипения.
Прямая FG — равновесие жидкой и газообразной фазы.
Участок FA — перегретая жидкость.
Участок F′A — растянутая жидкость (p<0).
Участок AC — аналитическое продолжение изотермы, физически невозможен.
Участок CG — переохлаждённый пар.
Точка G — точка росы.
Участок правее точки G — нормальный газ.
Площади фигуры FAB и GCB равны.
Красная — критическая изотерма.
K — критическая точка.
Голубые — сверхкритические изотермы
13) Расчет процессов с реальными газами






