При сравнении двух эталонов w1и w2заранее считается известным, что один из них первичен, а другой — вторичен. Мера первичного эталона переносится на вторичный эталон, которому приписывается и неизбежная ошибка сравнения. По этой причине эталоны одной и той же единицы измерения и одинакового значения меры образуют соответствующую иерархию — первичный эталон расположен в иерархии выше, а вторичный — ниже. Число уровней иерархии определяется соображениями практичности. На самом низком уровне находятся рабочие средства измерения, а перед ними — контрольные. Передача меры эталонам сверху вниз в пределах иерархии называется эталонированием [1]. Поскольку при этом мера эталона при переходе на более низкие уровни иерархии распространяется все шире, для этого все чаще употребляется определение пропагация эталонов [2]. На вторичный эталон переносится мера первичного, а из процесса сравнения устанавливается погрешность меры.
Рассмотрим пример, когда два сравниваемых эталона имеют приблизительно одинаковую меру. Первичный эталон w1обладает номинальной мерой w10, установленной в момент T0l времени эксплуатации первичного эталона. Неточность меры первичного эталона
(2.1)
описывает нестационарный случайный процесс { 
}:
, (2.2)
где g 1(T), h 1(T)— функции времени, характеризующие соответственно случайную и систематическую составляющие, { 
} — стационарный случайный процесс со средним значением, равным нулю, с единичной дисперсией и корреляционной функцией
(2.3а)
. (2.3б)
Здесь E[]—математическое ожидание, Т — время эксплуатации эталона, t‑ текущее время,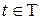 
.
По понятным соображениям номинальная мера эталона в момент T01 устанавливается так, чтобы эталон не был отягощен систематической погрешностью. Поскольку в процессе эксплуатации номинальное значение эталона может измениться на величину h 01(Т), которое по результатам исследований в период Т< T01 можно прогнозировать на время Т> T01 то
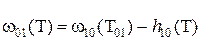, (2.4)
где 
— прогноз систематической погрешности. В дальнейшем для упрощения уравнения (2.1), (2.4) будем записывать так, что:
1. 
[3]). (2.5)
2. Систематическая погрешность h 1(Т),в уравнении (2.2) не включает составляющую с известным значением 
. Погрешность h 1(Т)по природе систематическая, но ее значение неизвестно. Источниками этой погрешности являются: систематическая погрешность вышестоящего эталона, по которому установлена мера 
; погрешности процесса сравнения при установлении меры эталона; погрешность учета составляющей (ошибка прогноза). Процесс возникновения этой погрешности будет рассмотрен позднее, при установлении меры вторичного эталона.
Систематическая погрешность h 1(Т)имеет следующие свойства:
а) постоянное значение
(2.6а)
в период использования эталона для калибровки вторичного эталона;
б) вероятность реализации значения h выражается плотностью вероятности
p h(h); (2.6б)
в) значение
; (2.6в)
г) значение систематической погрешности изменяется по времени Т вследствие, например, старения эталона, зависимости от Тдоверительного интервала прогноза и т. д.;
д) значение h 1неизвестно, т. е. его нельзя вводить в качестве поправки в меру эталона;
е) h 1можно рассматривать как случайную погрешность, снижающую достоверность меры эталона.
Случайная по природе погрешность эталона, обозначенная 
, определяется внутренними свойствами эталона, такими как осцилляция и флуктуация; при этом стандартное отклонение g 1зависит от времени Т ввиду изменений свойств эталона. Эта погрешность имеет распределение
. (2.7)
Аналогичным образом описывается неточность меры вторичного эталона:
; (2.8а)
. (2.86)
Сравнение эталонов производится в момент Т,по-разному расположенный на шкале времени эксплуатации каждого из образцов; например, если требуется установить меру вторичного эталона, то
T1>T0, T2<T0, (2.9а)
а если это периодическая поверка, то
T1>T0, Т2>Т0, (2.9б)
где Т0обозначает момент установления номинального значения эталона,
Т1 – время сравнения эталона w1, T2 — время сравнения эталона w2.
Сравнение эталонов осуществляется с помощью компаратора (см. рис. 2.1). Показание компаратора обозначено символом у;при этом истинное значение показания у 0 описывается выражением
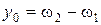, (2.10)
и оно неизвестно.
Рис. 2.1. Схемы сравнения двух эталонов с помощью компаратора для определения меры вторичного эталона
Компаратор вносит погрешность сравнения
, (2.11)
которую можно моделировать выражением (2.2), т. е.
. (2.12)
Поскольку мы рассматриваем случай передачи меры вторичному эталону, результат сравнения (уравнение измерения) имеет вид[4]:
(2.13)
Одноразовое сравнение
Случайные погрешности возникают в результате случайной реализации. После подстановки в уравнение измерения (2.13) выражений (2.1), (2.2), (2.8) и (2.12) получается
. (2.14)
Мера вторичного эталона может быть установлена на основе известных членов уравнения (2.14), к которым относится , а также 
, таким образом,
. (2.15)
Правильный результат должен быть следующим:
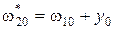, (2.16)
а это означает, что выявленная мера вторичного эталона отягощена погрешностью компаратора.
Уравнение погрешностей получается после вычитания из уравнения (2.14) истинного значения, т. е. уравнения (2.16):
(2.17)
Поскольку в уравнении (2.17) все члены являются одноразовыми реализациями случайных процессов, то они имеют постоянные значения, и Е(х)= х. Определяемая по уравнению (2.17) величина систематической погрешности вторичного эталона описывается выражением[5] (рис. 2.2)
. (2.18)
Принимая во внимание свойства источников погрешностей — членов выражения (2.18), можно определить значение математического ожидания и дисперсии систематической погрешности вторичного эталона, а именно:
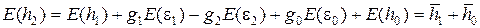, (2.19)
поскольку предполагалось, что средние значения процессов 
равны нулю, а также
var(h 2) = var(h 1) + var(h 0)+ g 12+ g 22+ g 32. (2.20)
Эти результаты требуют комментария. Значение систематической погрешности h 1 впервичном эталоне является элементом множества систематических погрешностей, соответствующих другим эталонам. Значение математического ожидания множества систематических погрешностей обычно близко к нулю (симметричная функция p (h 1)), но не всегда. Дисперсия h 1также является характеристикой множества погрешностей эталонов одинакового типа. Подобным же образом h 0 и var h 0характеризуют множество компараторов одного типа в одинаковых условиях, одного времени эксплуатации и для того же самого значения показания у.
Результат оценки дисперсии содержит в качестве составляющей дисперсию случайной погрешности вторичного эталона. Это естественно, так как в процессе сравнения эта погрешность возникла и учтена в определении погрешности. Выражение (2.18), представляющее собой сумму случайных процессов, пригодно для установления распределения вероятности погрешности, по природе систематической, но неизвестного значения, поскольку в соответствии с допущениями (2.6) распределения этих ошибок в принципе известны. Следовательно, при заданном доверительном уровне можно определить интервал недостоверности меры эталона.
Кроме названной недостоверности меры вторичный эталон при его использовании вносит случайную погрешность
, (2.21)
вследствие чего дисперсия недостоверности меры эталона составляет
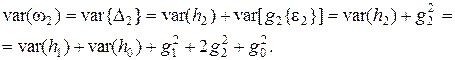(2.22)
Рис. 2.2. Схема распространения меры и погрешности первичного эталона на вторичный: а — процесс оценки; б — составляющие меры и погрешности
Поскольку дисперсия ошибки первичного эталона равна
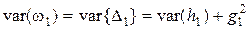, (2.23)
то из сравнения дисперсий (2.22), (2.23) следует
, (2.24)
т. е. неточность меры вторичного эталона больше неточности первичного эталона. Это иллюстрирует рис. 2.2. Кроме того, мера вторичного эталона должна включать величину погрешности компаратора.
