После введения отображений (1.35), (1.36) возникает вопрос о мере эквивалентности состояний а и а *. С учетом b*= f * (a) и a*= f *-1 (b*) получаем:
а * =f -1* [ f*(a) ] =a, (1.37)
т. е.
а Û а *. (1.38)
Вместе с тем данная эквивалентность существует в пределах способности различения, выраженной соотношением (1.36). Поскольку выбор решающего правила влияет на значение b * (а тем самым, по соотношению (1.30), и на состояние а *), то, как показано на рис. 1.6, может существовать много состояний a *, эквивалентных первичному состоянию а, и разность
а* - а = const (1.39)
может оказаться одинакова для любого из возможных решающих правил. Поэтому выбранная по решению D (1.27) точка b *не характеризует неоднозначность образа состояния а, полученного в результате измерения.
Использование множества {b*, ра(b*)} затруднительно и не всегда необходимо. Рассмотрим сначала пример pa = const; при этом из условия ∫ pa (b)d b = 1 вытекает, что
ра(b*)=1/(b в - b н ), (1.40)
если b ви b н означают верхний и нижний пределы множества Ва.
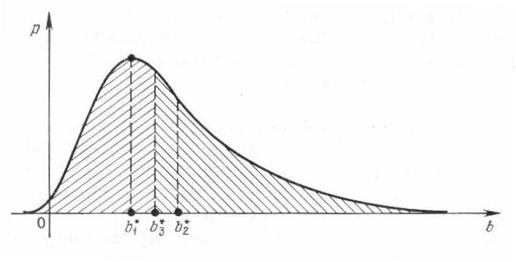
Рис. 1.6. Образы состояния а для правил решения D1, D2, D3
Неопределенность образа можно характеризовать удалением (отклонением) r(b*, b) элементов множества Ва от точки b*, если пространство В, в котором представлены случаи bÎВа, наделено метрикой.
С учетом предположения BÌ R пространство событий b ô а нормируемо, и в соответствии с используемыми нормами этого пространства отклонения r таковы:
|| х || =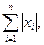 
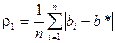; (1.41)
|| х || =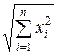 
, 
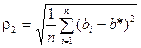; (1.42)
|| х || =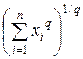 
, 
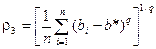(1.43)
и т.д.
Важным свойством отклонения является то, что область r определяет область в множестве В. Множество Ва с помощью точки b* упорядоченно разделено на два непересекающихся подмножества В н и В в, таких, что
В = В н È В в. (1.44)
Отклонения по типу (1.41) - (1.43) могут быть обозначены отдельно для множеств В н, В в как rн и rв соответственно.
Меры множеств
Иным способом выражения неоднозначности отображения состояния а взначение bÎВа для рассматриваемого случая ра(b)=1/(b в - b н ) является применение меры множества, например меры Лебега, меры Радона и т.д. Каждому из множеств В, В н, В в(1.44) по мере Лебега соответствуют значения
m(В н) = mн = b* - b н>0, (1.45а)
m(В в) = mв= b в - b *>0, (1.45б)
m(B) = m(B нÈ b* È B в) = mн+mв = 2m, (1.45в)
причем
m (В а) = b в - b н. (1.45г)
Если вероятность p a(b) ¹ const, что бывает чаще всего, то прямое нахождение меры ввиду неопределенности a = >{ b, pa (b)} весьма трудно. Такая мера должна состоять из малого числа параметров, быть легко уяснимой и, главное, не требовать для ее определения знания распределения вероятности ра(b). Дело в том, что некоторые распределения вероятностей, такие как экспоненциальное, геометрическое, распределения Пуассона и Стьюдента, описываются одним параметром, а нормальное, равномерное, биномиальное распределения - с помощью двух параметров, т.е. в общем случае
ра(b) = р(b, q1, q2, q3,...), (1.46)
где q1, q2... - параметры функции распределения вероятности.
Указание вида распределения, решающего правила D (1.27), выбора значения b*, а также одного или соответственно двух параметров полностью характеризуют b* и неоднозначность отображения (1.26). Важно, чтобы степень неоднозначности отображения можно было установить, не пользуясь распределением вероятности ра(b), а также чтобы ее смысл не зависел от типа распределения вероятности. Следует отметить, что такой меры, которая описывала бы ту или иную неоднородность более однородно, не существует, если потеря информации о неоднородности не компенсируется дополнительной информацией. Поэтому для характеристики неоднозначности отображения применяется ряд частичных мер, неполных в сравнении с ра(b), но каждая из них выражает эту неоднозначность в каком-либо более узком смысле.
